计算机组成原理(2)--进位计数制、BCD码，有符号数和无符号数、浮点数

目录

一、进位计数制：

 二、BCD码：

1、8421码：

2、另外的两种码制：(了解)

 三、无符号整数的表示和运算：

1、无符号数表示：

​编辑 2、无符号数的加减法：

 四、带符号整数的运算：

1、原码：

 2、反码与补码：

​编辑

3、补码的计算：

 1、补码的加法：

 2、补码的减法：

 4、移码：

5、奇偶校验码：

6、定点整数与定点小数表示范围：

五、浮点数： 

 1、浮点数的表示：​编辑​编辑

 2、浮点数规格化：

​编辑 3、IEEE 754标准：

1、移码：

2、IEEE754标准：

 3、IEEE754特殊表示范围：

---

一、进位计数制：

1、基数：每个数码位所用到的符号的个数，r进制数基数是r。

2、真值：我们常说的带正负号的数。 例：-1，12

3、机器数：把正负号数字化的数，也就是存在计算机内部的数。(二进制位第一位表示符号这种)

二级制各个位置上的值

各个进制的表示：

 十进制转化为二进制：75.3为例：

整数部分：从下向上写

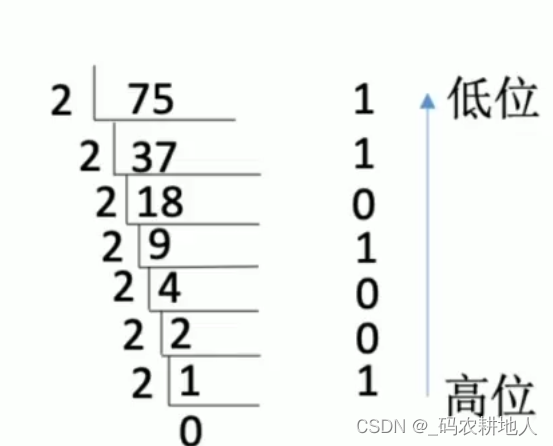
 小数部分：从上向下写

---

 二、BCD码：

用四位二进制数来表示一位十进制数。

1、8421码：

四位二进制数最多表示16个数，但是十进制数只有0-9所以会有6个冗余字段，即1010-1111内没有定义任何十进制数。

在计算机内实现8421码的加法：

1、如果结果不在0000-1001内，则给结果+6即0110所得的数在前面补0凑齐位数。

2、如果结果在定义的0000-1001内可直接计算。

2、另外的两种码制：(了解)

---

 三、无符号整数的表示和运算：

整体总结：

1、无符号数表示：

1、计算机通用寄存器的字长决定了计算机无符号位数的上限，n位机器最大表示2^n -1

2、无符号数用全部位数来表示数字，没有符号位。

3、最大数字是全1，最小是全0。

2、无符号数的加减法：

加法： 直接按位相加。

减法：减数按位取反，末尾加1，所得数与被减数进行加法运算

 

---

 四、带符号整数的运算：

整体总结：

1、原码：

原码不能用于两个数字的计算，因为符号位不能参与运算。因此需要用补码来进行真值的计算。

 2、反码与补码：

• 正数的原码、反码、补码相同。
• 负数的反码在原码的基础符号位不变上按位取反，0变1，1变0.
• 负数的补码在反码的基础上符号位不变末尾加1

负数的原码转化为补码的快速方法：

从右向左找到第一个1，从它的左边第一位到符号位之间的所有数按位取反即可。符号位是不取反的。

3、补码的计算：

符号位也参与运算，如果有溢出只取运算的那几位。

例：4位补码数1100和0100相加结果是1 0000，但是由于数是四位，所以最终结果为0000。

 1、补码的加法：

 2、补码的减法：

首先将减数转化为其相反数，即A-B = A+(-B).

补码的转化：

常规法：全部位取反，末尾+1. 是全部位，符号位也要取反。

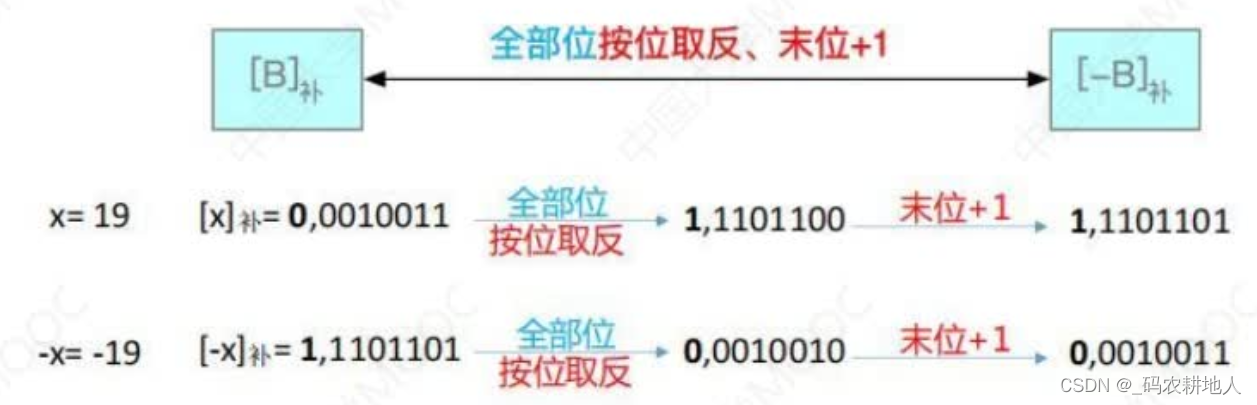
快捷法：从右向左找到第一个1，其左边的全部位都按位取反，包括符号位。

上面的19. 0001 0011，从右向左第一个1在第一位，所以将其左边的数全部取反，右边的数不变即其补码的相反数。  1110 1101

 4、移码：

将补码的符号位取反即得到移码：移码只能表示整数。

5、奇偶校验码：

 1、保证传输数据中的1的个数为奇数或偶数个。奇校验保证为奇数个，偶校验保证1的个数为0数个。

2、检验原理：将接收到的数据进行个信息位的异或运算。如果结果是0表示传输正确，如果是1表示传输错误。

3、奇偶校验只能保证传输过程中有奇数个位置发生错误，不能检验出偶数个位置发生错误。

4、奇偶校验只能检错不能纠错。

6、定点整数与定点小数表示范围：

补码中只有一个+0没有-0，-0表示一个最小的负数。八位二级制数补码1 000 0000表示-128

        对于8位二进制数，补码的表示范围是-128~+127，而原码和反码的表示是-127~+127.所以对于-128来讲这个补码不能用8位二进制用原码反码表示，因为反码和原码对于八位来讲最小是-127。

---

五、浮点数： 

 浮点数的引出主要是为了表示更大的数，浮点是类似于十进制数的科学计数法。

 1、浮点数的表示：

 2、浮点数规格化：

3、IEEE 754标准：

1、移码：

移码 = 真值+偏移值。 这个偏移值是认为定义的，在前面的计算中偏移值取的是2^n，但是在IEEE754标准中，偏移值取2^n -1

计算时仍是将补码的符号位取反求得移码，然后移码结果再-1即可。

2、IEEE754标准：

一位数符，八位阶码(移码表示)，23位数值位(原码表示)

因为尾数用原码表示，所以根据浮点数的规格化，无论是正数还是负数，小数点后第一位必须是1，所以我们这个1默认有，但是不存，所以下图写的尾数数值位23位但实际是24位，因为那个默认的1未存。

阶码的-127和-128不用于表示数，所以阶码最小是-126

 将浮点数转化为IEEE754标准案例：

1、将浮点数转化为标准形式 -1.1*2^-1  负数的原码必须是1.1****

2、确定阶符 1

3、去掉最高位的1确定真值部分 .1000......

4、确定阶码的移码： 阶码是-1所以补码是1111 1111 移码是0111 1110

5、将数据按规定的位数配对即可。

 将IEEE754标准转化为真值：

计算阶码的真值 = 移码 - 偏移量 (和十进制一样计算)

 3、IEEE754特殊表示范围：

1、标准表示：

 2、特殊值表示：