25分钟详细解说c++搜索算法

🏆今日学习目标：
🍀1理解搜索思路
🍀2学会搜索模板
✅创作者：贤鱼
🎉个人主页：贤鱼的主页
🔥专栏系列：c++

🔥深度优先搜索

了解原理

以深度为优先的搜索算法，可以理解为一条路走到黑
图例解释
==现在需要从蓝色五角星走到红色五角星

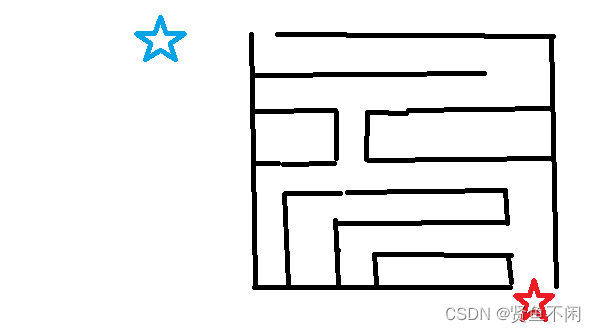
理想走法：



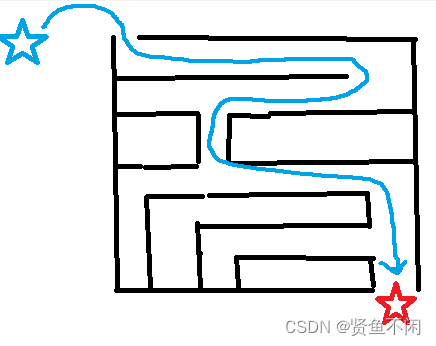
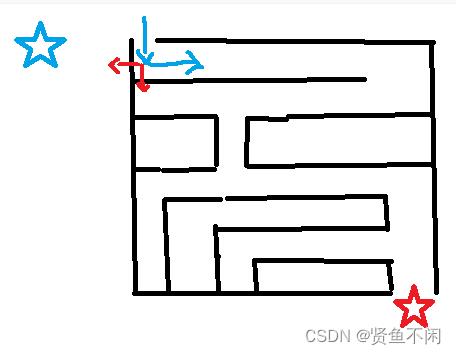
很明显，这里直走到头已经走不了了，才会从之前的岔路拐弯（一路走到黑）




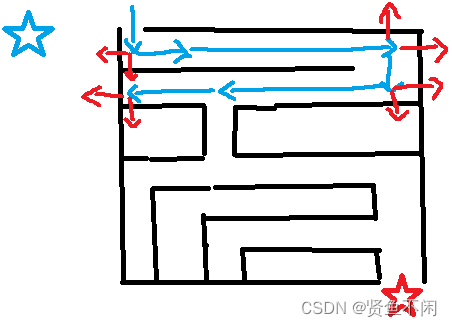
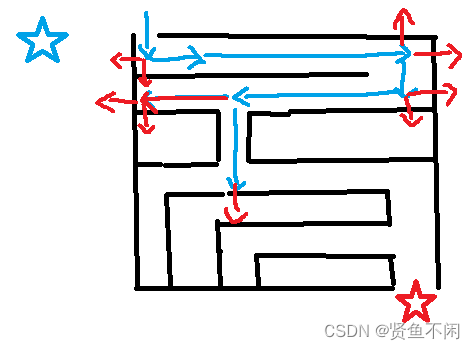
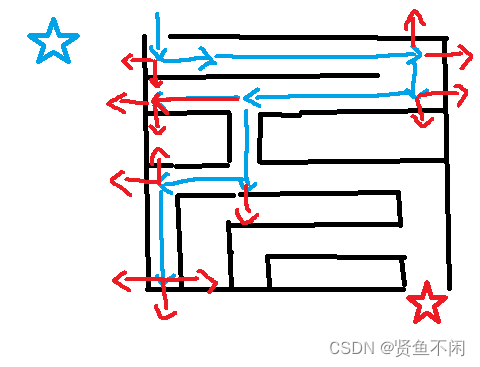
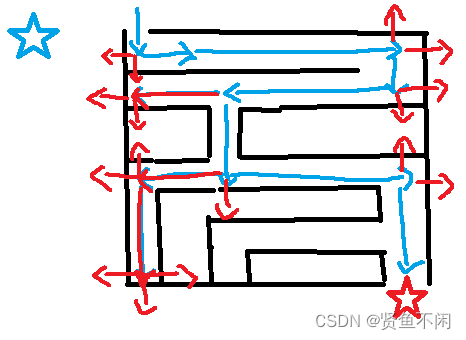
这就是深度搜索走迷宫的全过程，当然，深度优先搜索不只是光能走迷宫，其他的例题后面会讲

方向数组

一般会定义两个数组

int dx[5]={0,1,-1,0,0}
int dy[5]={0,0,0,1,-1}
1
2

这里我一般喜欢让数组下标从1开始，所以第一个0只是顶替个位置

for(int i=1;i<=4;i++){
	int tx=dx[i]+x;
	int ty=dy[i]+y;
}
1
2
3
4

这里xy是原来的坐标，txty是走后的坐标，一般题目要求是上下左右四个方向走，如果要求斜方向也可以走方向数组会有些变化

int dx[8]={0,1,-1,0,0,1,-1,-1,1}
int dy[8]={0,0,0,1,-1,1,-1,1,-1}
1
2

函数

函数的类型在本章需要的主要有两种：
int类型和void类型
前者有返回值，可以处理各种类型的题目，后者没有返回值，常用于走迷宫一类的题。

递归

还是看上方的图，只有走到死路的时候会往前走其他的路，这个过程就是递归的过程

🍀套用模板

void dfs(int x,int y){
if(x==xx&&y==yy)//到终点了
	return；//void类型返回值为空
for(int i=1;i<=4;i++){
	int tx=dx[i]+x;
	int ty=dy[i]+y;
	if() continue//这里判断有没有出界，有没有走过，有没有碰到墙之类的
	//如果没有就继续
	vis[tx][ty]=1//记录一下走没走过，避免重复走，如果不记录会死循环，上下上下不停地走
	dfs(tx,ty);
}
}
1
2
3
4
5
6
7
8
9
10
11
12

🔥广度优先搜索

以广度为优先的搜索，可以理解为在每一步的时候处理所有的可能性
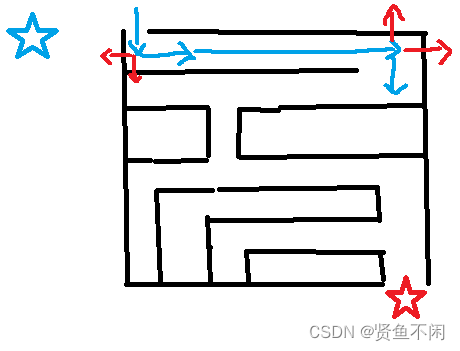
还是来看看图：

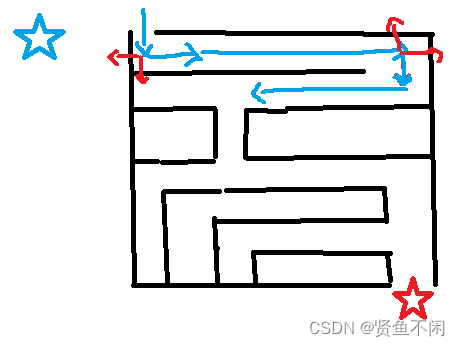
可以看到这里遇到了岔路




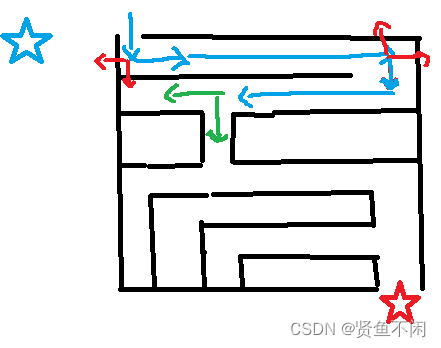
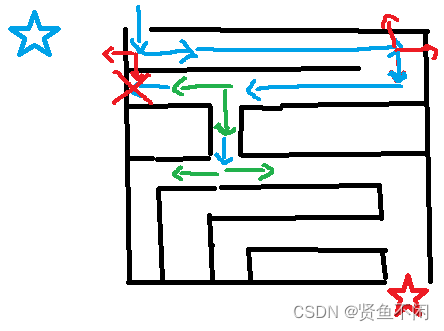
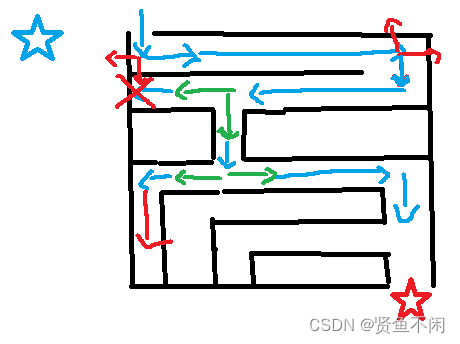
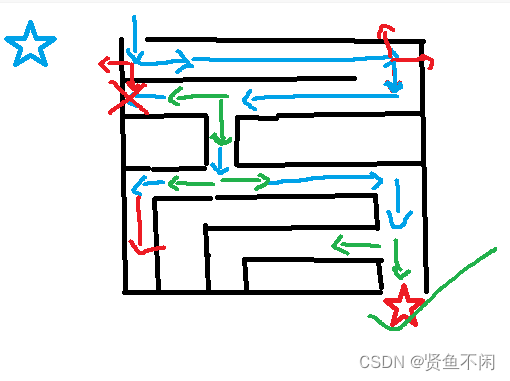
我们在这里同时处理

了解原理

队列

特点 先进先出：可以理解为一个联通的钢管，先放进去的部分先掉下来

手打队列

void bfs(){
	head=0;tail=1;//这里是记录头和尾的坐标，如果t加1，也就是入队的过程，如果h加1，就是出队的过程
	qw[0][0]=1;
	a[tail]=0,b[tail]=0;
	while(tail!=head){
		head++;
		for(int i=1;i<=4;i++){//下面部分基本一样
			int tx=a[head]+dx[i];
			int ty=b[head]+dy[i];
			if() continue;
			tail++;
			a[tail]=tx;//这里入队并且记录数据
			b[tail]=ty;
			qw[tx][ty]=1;//避免走重复，和上文一样，避免死循环，不过广搜不是很影响
			if(到终点){
				return;
			}
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

queue

struct aaa{
	int x,y;
};//记录一下结构体，具体下面有介绍
1
2
3

void bfs(){
	vis[x][y]=1;
	dis[x][y]=0;
	queue <aaa> q;//aaa是结构体的类型，这句话的意思是定义一个类型为aaa的队列
	q.push((aaa){x,y});//入队的意思，第一个括号写类型，因为结构体是aaa类型，xy是int类型，后面是入队数据
	while(!q.empty()){//这句话的意思是当队列不为空（empty是为空的意思，！取反）
		aaa a;//定义一个aaa类型的变量a
		a=q.front();//这个意思是取出队首元素，也就是队列中最先进去的
		q.pop();//取出队首元素后出队，将已经取出的元素扔掉
		for(int i=1;i<=4;i++){
			int tx=a.x+dx[i];
			int ty=a.y+dy[i];
			if() continue;
			q.push((aaa){tx,ty});//入队的意思，和上文h，t作用一样
			vis[tx][ty]=1;//记录路径，避免重复
			if(到终点){
				return;
			}
		}

	}
	return ;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

结构体

struct aaa{
	int x,y;
};
aaa a;//定义一个aaa类型的a
a.x;
a.y;这样可以方便记录数据
a[i],b[i];当然，这样子记录xy坐标也是可以的，但是有些麻烦
1
2
3
4
5
6
7

🍀套用模板

void bfs(){
	入队
	while（队列不为空）{
		取出队首元素
		出队
		for（1 to 4）{
			和上文深搜走迷宫一样
			如果可以走{
				入队元素
			}
			如果到终点{
				return；
			}
		}
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

🏆结束语 搜索不光可以走迷宫，其他具体的题目题解可以看到专栏内容