暴力破解Leetcode 42：接雨水问题

题目描述

问题描述 给定一个整形数组arr，已知其中所有的值都是非负的，将这个数组看作一个柱子高度图，计算按此排列的柱子，下雨之后能接多少雨水。(数组以外的区域高度视为0)
数据范围：1≤n≤1000000，数组中每个值满足 >=0 
示例 
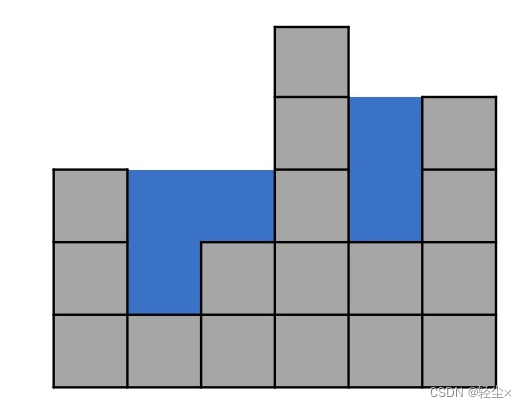
输入：[3,1,2,5,2,4]

返回值：5

说明：数组 [3,1,2,5,2,4] 表示柱子高度，在这种情况下，可以接 5个单位的雨水，蓝色的为雨水

 

 分析

定性分析

正如一个巴掌拍不响，一根、两根柱子存不住水，想要存住水，至少需要三根柱子，且形状要满足“凹”型，意味着某个柱子想要存水，它的左边和右边均必须至少要有一根高于自身高度的柱子

具体到每根柱子，分析如下：

• 0号柱子，因为它左边没有比它高的柱子，所以它不能存水
• 1号柱子，它左边的柱子只有一根，是0号，比它高，它的右边有四根柱子均比他高，所以它能存水
• 2号柱子，它左边有两根柱子，但只有0号柱子比它高，右边有三根柱子，其中有两个比它高，满足两边均至少有一根高于自身这个条件，所以它也能存水
• 3号柱子，一柱擎天，左右两边都没有比它高的柱子，所以它不能存水
• 以此类推，4号柱子，左右各有一根柱子比它高，能存水
• 5号柱子，满足左边有1根柱子比它高，但它的右边是空的，不满足两边均至少有一根高于自身这个条件，所以它不能存水

定量分析

上面定性的分析了能不能存水的条件，接下来定量的分析一下能存多少水的问题

能不能存水取决于能否构成“凹”型，能存多少水取决于“凹”型两边的高度，且根据木桶效应：一个木桶能装多少水，取决于最短的那块板。“凹”型能存多少水，也取决于两边最低的那根柱子。

• 0号柱子，不能存水，存水量为0
• 1号柱子，它所在的“凹”型由0号柱子、1号柱子以及3号柱子构成，因为左边最高的柱子为0号，右边最高的为3号，根据木桶效应存水量取决于较短的那根柱子，3号柱子高为5，0号柱子高度仅为3，所以1号柱子的存水量取决于0号，水量为(1号柱子的高度-自身高度)，即：3-1=2；
• 2号柱子，它所在的“凹”型由0号柱子、2号柱子以及3号柱子构成，存水量由较短的0号柱子决定，水量为(2号柱子的高度-自身高度)，即：3-2=1；
• 3号柱子，不能存水，存水量为0
• 4号柱子，它所在的“凹”型由3号柱子、4号柱子以及5号柱子构成，存水量由较短的5号柱子决定，水量为(5号柱子的高度-自身高度)，即：4-2=2；
• 5号柱子，不能存水，存水量为0

总的存水量为2+1+2 = 5。

代码实现

有了上面的分析思路，就可以尝试用代码来实现，语言无关，这里用java来实现。

大概的思路就是：为每一根柱子寻找左边、右边最高的柱子，通过高度对比判断能否组成“凹”，如果能计算水量并叠加。

具体如下

1、定义一个变量记录总雨水值

  int res = 0;// 总雨水量

2、获取原数组长度，即总共有多少柱子

 int length = inputArr.length;// 数组长度

3、定义一个数组记录每一根柱子左边最高柱子的高度

int[] left = new int[length];

4、再定义一个数组记录每个柱子右边最高柱子的高度

int[] right = new int[length]

5、遍历每一根柱子，找到其对应左边最高柱子的高度

 for (int i = 1; i < length; i++) {
    left[i] = Math.max(left[i - 1], inputArr[i - 1]);
}

因为0号柱子左边没有柱子，不用参与变量，它左边的柱子高度默认为0，所以从1号柱子开始循环，每一根柱子左边最高的柱子，要么是上一个最高的(left[i-1])，要么就是当前柱子(inputArr[i])的左边那个(inputArr[i-1])。

比如1号柱子，它的左边最高柱子高度 = Math.max(left[1 - 1], inputArr[1 - 1])，left[0]取得是默认值0，所以它左边最高的柱子高度取inputArr[0 ]，也就是3，即left[1]=3；

2号柱子，它的左边最高柱子高度 = Math.max(left[2 - 1], inputArr[2 - 1])，即上一轮中最高的与相邻左边柱子中最大的那个，显然left[1]>inputArr[1]，所以left[2] = left[1]，也就是3；

同理，其他的柱子右边最高柱子高度都可以这样算出来，只是方向相反而已。

 
        for (int j = length - 2; j >= 0; j--) {
            right[j] = Math.max(right[j + 1], inputArr[j + 1]);
        }

相同的原因，inputArr[length-1]号柱子右边没有柱子，默认值为零，从length-2开始变遍历

计算水量

经过两个循环的变量，已经将每根柱子左边、右边最高的柱子高度都获取到了，接下来我们只需要再将所有柱子都循环一遍，结合上面两个数组来判断是否能形成“凹”型，如果能，顺便把水量算出来叠加。

 
        for (int i = 0; i < length -1; i++) {
 
            int min = Math.min(left[i], right[i]);//寻找较短的那块板
 
            if (min > inputArr[i]) {//是否能形成“凹”型
                res += (min - inputArr[i]);// 叠加雨量
            }
 
        }

把数据套进去验证一下：

• left[0]=0，right[0]=5，min= 0，inputArr[0]=5，不能形成“凹”
• left[1]=3，right[1]=5，min= 3，inputArr[1]=1，能形成“凹”，水量为3-1=2
• left[2]=3，right[2]=5，min= 3，inputArr[2]=2，能形成“凹”，水量为3-2=1
• left[3]=3，right[3]=4，min= 3，inputArr[3]=5，不能形成“凹”
• left[4]=5，right[4]=4，min= 3，inputArr[4]=2，能形成“凹”，水量为4-2=2
• left[5]=5，right[5]=0，min= 0，inputArr[4=4，不能形成“凹”

res = 2+1+2 = 5

完整代码

package com.learn.leetcode;
 
 
public class MaxWater {
 
 
    public static void main(String[] args) {
        int[] inputArr = {3,1,2,5,2,4};
        int result = countWater(inputArr);
        System.out.println("总雨水量为：  " + result);
    }
 
    private static int countWater(int[] inputArr) {
 
        int res = 0;// 总雨水量
 
        int length = inputArr.length;// 数组长度
        int[] left = new int[length];// 记录每个元素左边最高柱子
 
        int[] right = new int[length];// 记录每个元素右边最高柱子
 
        for (int i = 1; i < length; i++) {
          
            left[i] = Math.max(left[i - 1], inputArr[i - 1]);// 当前数字左侧最大的数字
        }
 
        for (int j = length - 2; j >= 0; j--) {
           
            right[j] = Math.max(right[j + 1], inputArr[j + 1]);//当前数字右侧最大的数字
 
        }
 
        for (int i = 0; i < length -1; i++) {// 计算雨水量
 
            int min = Math.min(left[i], right[i]);//寻找较短的那块板
            if (min > inputArr[i]) {//是否能形成“凹”型
                res += (min - inputArr[i]);// 叠加雨量
            }
 
        }
 
        return res;
    }
 
 
}

小优化

上面三个循环其实可以优化成两个，第三个可以合并在第二个里，因为每根柱子左边最大的高度确定了时，只要确定一根右边的柱子就可以计算一根，优化后的代码如下：

package com.learn.leetcode;
 
 
public class MaxWater {
 
 
    public static void main(String[] args) {
        int[] inputArr = {3,1,2,5,2,4};
        int result = countWater(inputArr);
        System.out.println("总雨水量为：  " + result);
    }
 
    private static int countWater(int[] inputArr) {
 
        int res = 0;// 总雨水量
 
        int length = inputArr.length;// 数组长度
        int[] left = new int[length];// 记录每个元素左边最高柱子
 
        int[] right = new int[length];// 记录每个元素右边最高柱子
 
        for (int i = 1; i < length; i++) {
 
            left[i] = Math.max(left[i - 1], inputArr[i - 1]);//当前数字左侧最大的数字
        }
 
        for (int j = length - 2; j >= 0; j--) {
            right[j] = Math.max(right[j + 1], inputArr[j + 1]);//当前数字右侧最大的数字
 
            int min = Math.min(left[j], right[j]);//寻找较短的那块板
 
            if (min > inputArr[j]) {//是否能形成“凹”型
                res += (min - inputArr[j]);// 叠加雨量
            }
        }
 
        return res;
    }
 
 
}

以上就是暴力破解接雨水问题的全部内容，更优雅的实现方式待下回分解，思想在，实现方法就可以有多种多样。