【排序算法】计数排序（C语言）

【排序算法】—— 计数排序（C语言）

一、计数排序原理

​ 计数排序、桶排序、基数排序都是非比较的排序，在实际应用中基数排序和桶排序的实用价值不高，所以在这里我们实现计数排序即可

​ 计数排序又称鸽巢原理，是对哈希直接定址法的变形应用。

​ 计数排序的实现原理是统计相同元素出现的次数，并开辟一个新数组，将该元素的次数写在新数组元素值下标位置，遍历新数组将下标依次写入源数组，写入下标的次数就是新数组种对应位置存储的相同元素出现的次数，以此来实现排序。

1. 计数：开辟新数组temp，遍历原数组arr，将arr中元素出现的次数写入temp中该元素值下标的位置上

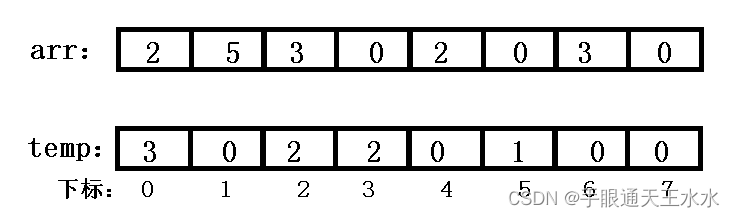
2. 排序：遍历temp数组，将数组下标作为元素值依次写入arr数组，每个下标写入的次数就是对应下标位置的元素值；

二、计数排序实现思路

上面描述的就是计数排序的基本原理，但是采用的是直接映射的原理，若是待排数组是100，105，103，108，107那么就要最少创建长度为108的数组，而且其中前100个位置是没有被使用的，并且数组中出现了负数也无法使用，所以采用直接映射的方式并不合适。

对此我们将使用相对映射的原理，先找出待排数组的最大值和最小值，创建新数组的大小就是最大值和最小值的差加一，保证数组0下标是最小值，数组最后一个下标是最大值。计数时将元素值减最小值后计入对应下标的位置，排序时，将新数组的下标加上最小值就能得到原数组的元素，从而实现排序

1. 遍历数组，获取原数组arr的最大最小值，最大值max = 2，最小值min = -4

2. 计数：开辟一个max - min + 1大小的空间，将元素减最小值再在对应下标位置写入元素出现次数

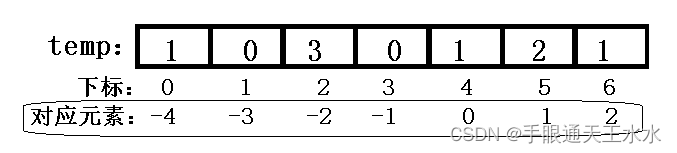
3. 排序：遍历数组temp，依次将下标加上最小值写入原数组，写入次数就是数组中的元素出现次数，排序结束

三、代码实现

void CountSort(int* arr, int size)
{
    //找最大最小值
    int i = 0;
    int max = arr[0], min = arr[0];
    for (i=1; i<size; i++)
    {
        if (arr[i] > max)
        {
            max = arr[i];
        }
        if (arr[i] < min)
        {
            min = arr[i];
        }
    }
    
    //计数
    int range = max - min + 1;
    int* temp = (int*)calloc(range, sizeof(int));
    if (temp == NULL)
    {
        perror("calloc fail!\n");
        return;
    }
    
    for (i=0; i<size; i++)
    {
        temp[arr[i]-min]++;	//记录每个元素出现的次数
    }
    
    //排序
    int j = 0;
    for (i=0; i<range; i++)
    {
        while (temp[i] > 0)
        {
            arr[j] = i + min;	//将元素下标还原并写入原数组
            j++;
            temp[i]--;
        }
    }
    
    free(temp);
    temp = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

四、计数排序的特点

优点：

1. 计数排序在范围集中时的排序效率很高，但是使用场景有限

缺点：

1. 计数排序只能对于整数类型进行排序
2. 计数排序对于数据范围跨度大的数据排序时空间效率很低

• 时间复杂度：$O(MAX(N,范围))$
• 空间复杂度：$O(范围)$
• 稳定性：稳定（由于计数排序只能排整数，所以它的稳定性并没有太大意义）