第一章学习

第一章 命题与命题公式

1.命题与命题公式

2.命题公式的等值演算

命题变元

命题变元是不是命题,不是命题又被称作什么?

命题的概念
整句话是陈述句& 能判断真假
1
2
3
4

争议:符号化也是命题
解释:可以用符号表示一个命题,这样那个符号就代表命题
eg: 小王今天去李四家喝茶(这满足陈述句,能判断真假,所以是个命题) ,设P:小王今天去李四家喝茶 ,问: P是个命题(V)

争议:命题变元为什么不是命题
解释:若某命题P是变化的,则是命题变元,若命题中不存在不确定因素,则是命题常项
eg: 小王在家做试卷,算出X+5=7(这满足陈述句,能判断真假,所以是个命题)
设P:小王在家做试卷,算出X+5=7 ,问: P是个命题(V/X)(因为X不是确定值,若X不是2,则这是个假命题)

合式公式(命题公式)

什么叫做命题的合式公式?

概念
命题+联结词+括号=命题的合式公式

说明
1.	原子命题变元是最简单的合式公式,称为原子合并公式,称为原子公式
2.	命题公式没有真值,只有对其命题变元进行真值指派后,方可确定命题公式的真值
3.	整个公式的最外层可以省略:公式中不影响运算次序的括号也可以省略
4.	在实际应用中,为了方便存储和运算,命题公式常用二元树的方式来表示
1
2
3
4
5
6
7
8
9
10

合式公式的面部特征

1.命题变元P本身是一个公式(比如 P,Q,R…),所以﹁ P也是公式 ,如(﹁P, ﹁Q, ﹁R…)
2.如果G,H是公式,则(G∧H) , (G∨H),(G ->H), (G <->H )也是公式

仅由有限步使用规则 (1),(2),(3)后所得到的包含命题变元,联结词和括号串才是命题公式  比如:  ﹁(P∧Q)  <-> R ,反复利用上面的三条,才是命题公式 
1
2
3
4

命题公式定律

双重否定律：	A ⇔ ¬¬A
幂等律：	A ⇔ A∧A，A ⇔ A∨A
结合律：	(A∧B)∧C ⇔ A∧(B∧C )
		(A∨B)∨C ⇔ A∨(B∨C )
交换律：	A∧B ⇔ B∧A
		A∨B ⇔ B∨A
分配律：	A ∨ (B∧C) ⇔ (A∨B) ∧ (A∨C)
		A ∧ (B∨C) ⇔ (A∧B) ∨ (A∧C)
		
吸收律：	A∨(A∧B ) ⇔ A
A∧(A∨B ) ⇔ A

德摩根律：	¬(A∨B )  ⇔ ¬A∧¬B   用取反的意思记
¬(A ∧ B )  ⇔ ¬A ∨ ¬B

同一律：	A ∨ F ⇔ A，A ∧ T ⇔  A
零律：	A ∨ T ⇔  T，A ∧ F ⇔ F

排中律：	A ∨ ¬A ⇔  T 实集
否定律：	A ∧ ¬A ⇔  F 空集

蕴涵等值式：	A → B ⇔ ¬A ∨ B
等价等值式：A ↔ B  ⇔ （A → B）∧（ B → A）

假言易位：A → B ⇔  ¬B → ¬A
等价否定等值式：A ↔ B ⇔ ¬ A ↔ ¬B
归谬论：（A → B）∧（ A → ¬B） ⇔  ¬A 可用罪名来记
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

命题公式运算顺序

()   ¬,  ∧,  ∨, → , ↔
1

指派

定义: 设P1 ,P2 ,P3 ,…Pn  是出现在公式G中的所∨∧→↔））有命题变元,指定P1 ,P2 ,P3  ,…Pn 的值,
则这组真值称为G的一个解释,常记为l ,  所以引出了真值表(不同的指派对命题不同的真值T/F)

Example:若有公式: G=  P →(¬Q∧R)
I1: P=0,Q=1,R=0是G的一个解释,使得G的真值为1(T)
I2: P=1,Q=0,R=0是G的一个解释,使得G的真值为0(F)




1
2
3
4
5
6
7
8
9
10

真值表的写法

有n个命题变元,则应有2ⁿ个不同的解释
eg: 3个变元, 2³ = 8个值

命题公式分类：通过查看真值表，真值为真的个数来区分

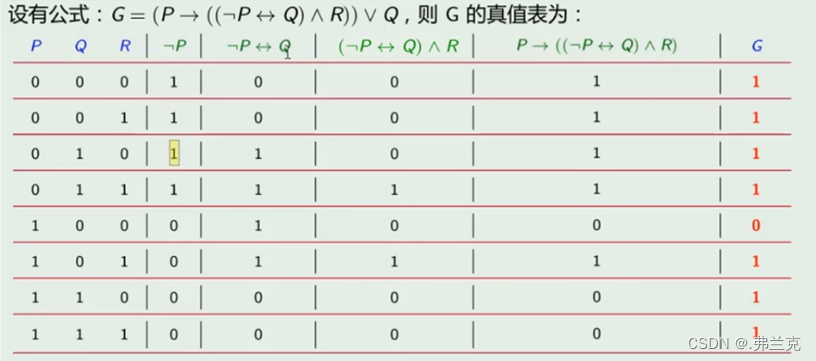
重言式

公式所有的结果真值都是真
1

矛盾式

公式所有的结果真值都是假
1

可满足公式

如果公式结果不是永假的
1

三种特殊公式之间的关系

1. G是永真的当且仅当¬G是永假的
2. G是可满足的当且仅当至少有一个解释I,使G在I下为真
3. 若G是永真式,则G一定是可满足式,但反之可满足公式不一定是永真式

公式的等价

只是在关系上代表等价,比如左式⟺右式, ⟺只是代表其关系,不能用作运算

若左右的真值结果相同,才称其等价
只要存在一组P,Q 真值不相等,则公式就不等价

eg: 因知G1=G↔H,由于G1是永真式,又根据等价联结词的定义G,H必须同真/同假,此时我们称G,H具有逻辑等价关系
1
2
3
4
5
6

公式等价的充分必要条件

对于任意两个公式G和H, G = H的充分必要条件是公式G↔H是永真公式

必要性:假定命题G=命题H,则命题G,命题H在其任意解释I下同为真/同为假,由于↔的意义得知,
公式G↔H在任何解释I下 ,其真值为”真”,即G↔ H为永真公式
                                                         
充分性:假定公式G↔ H为永真公式 , I是它的任何解释, 在I下, G↔H为真 因此若命题G,则命题H 同为真/同为假,
由于I的任意性,故有命题G  = 命题H 
1
2
3
4
5
6
7

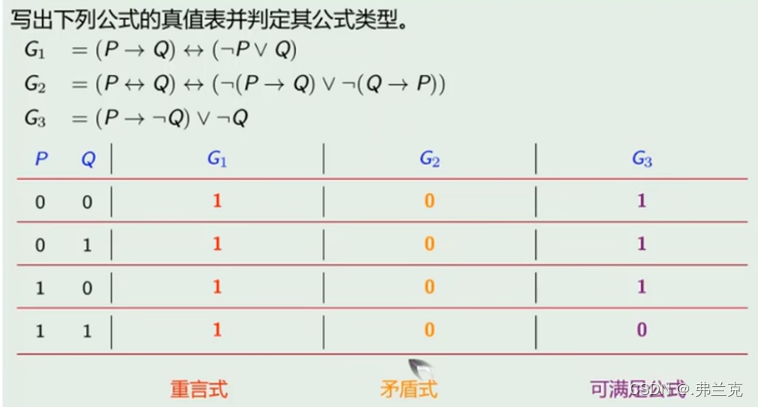
验证等价的方法

1.比较两边的真值表
2.左右化简(运用公式定律.化左/化右/同时化) ,而这个过程叫作等值演算