数据结构刷题：第十一天

目录

 一，二叉树的层序遍历

 1，广度优先搜索

思路和算法

复杂度分析

二，二叉树的最大深度

 1，深度优先搜索

思路与算法

复杂度分析

2，广度优先搜索

思路与算法

复杂度分析

三，对称二叉树

 1，递归

思路和算法

复杂度分析

2，迭代

思路和算法

复杂度分析

 一，二叉树的层序遍历

102. 二叉树的层序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-level-order-traversal/?plan=data-structures&plan_progress=ggfacv7

 1，广度优先搜索

思路和算法

我们可以用广度优先搜索解决这个问题。

我们可以想到最朴素的方法是用一个二元组 (node, level) 来表示状态，它表示某个节点和它所在的层数，每个新进队列的节点的 level 值都是父亲节点的 level 值加一。最后根据每个点的 level 对点进行分类，分类的时候我们可以利用哈希表，维护一个以 level 为键，对应节点值组成的数组为值，广度优先搜索结束以后按键 level 从小到大取出所有值，组成答案返回即可。

考虑如何优化空间开销：如何不用哈希映射，并且只用一个变量 node 表示状态，实现这个功能呢？

我们可以用一种巧妙的方法修改广度优先搜索：

首先根元素入队
当队列不为空的时候
求当前队列的长度 s_i
​依次从队列中取 s_i个元素进行拓展，然后进入下一次迭代

它和普通广度优先搜索的区别在于，普通广度优先搜索每次只取一个元素拓展，而这里每次取 s_i
​个元素。在上述过程中的第 i 次迭代就得到了二叉树的第 i 层的 s_i个元素。

为什么这么做是对的呢？我们观察这个算法，可以归纳出这样的循环不变式：第 i 次迭代前，队列中的所有元素就是第 i 层的所有元素，并且按照从左向右的顺序排列。证明它的三条性质（你也可以把它理解成数学归纳法）：

初始化：i=1 的时候，队列里面只有 root，是唯一的层数为 1 的元素，因为只有一个元素，所以也显然满足「从左向右排列」；
保持：如果 i=k 时性质成立，即第 k 轮中出队 s_k的元素是第 k 层的所有元素，并且顺序从左到右。因为对树进行广度优先搜索的时候由低 k 层的点拓展出的点一定也只能是 k+1 层的点，并且 k+1 层的点只能由第 k 层的点拓展到，所以由这 s_k个点能拓展到下一层所有的s_k+1个点。又因为队列的先进先出（FIFO）特性，既然第 k 层的点的出队顺序是从左向右，那么第 k+1 层也一定是从左向右。至此，我们已经可以通过数学归纳法证明循环不变式的正确性。

终止：因为该循环不变式是正确的，所以按照这个方法迭代之后每次迭代得到的也就是当前层的层次遍历结果。至此，我们证明了算法是正确的。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector <vector <int>> ret;
        if (!root) {
            return ret;
        }
 
        queue <TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            int currentLevelSize = q.size();
            ret.push_back(vector <int> ());
            for (int i = 1; i <= currentLevelSize; ++i) {
                auto node = q.front(); q.pop();
                ret.back().push_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
        
        return ret;
    }
};
 

复杂度分析

记树上所有节点的个数为 n。

时间复杂度：每个点进队出队各一次，故渐进时间复杂度为 O(n)。

空间复杂度：队列中元素的个数不超过 n 个，故渐进空间复杂度为 O(n)。

去看看这个

BFS 的使用场景总结：层序遍历、最短路径问题 - 二叉树的层序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-level-order-traversal/solution/bfs-de-shi-yong-chang-jing-zong-jie-ceng-xu-bian-l/

二，二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-depth-of-binary-tree/?plan=data-structures&plan_progress=ggfacv7

 1，深度优先搜索

思路与算法

如果我们知道了左子树和右子树的最大深度 ll 和 rr，那么该二叉树的最大深度即为max(l,r)+1

而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};
 

复杂度分析

时间复杂度：O(n)，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。

空间复杂度：O(height)，其中 height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

2，广度优先搜索

思路与算法

我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，最后我们用一个变量 ans 来维护拓展的次数，该二叉树的最大深度即为 ans。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        queue<TreeNode*> Q;
        Q.push(root);
        int ans = 0;
        while (!Q.empty()) {
            int sz = Q.size();
            while (sz > 0) {
                TreeNode* node = Q.front();Q.pop();
                if (node->left) Q.push(node->left);
                if (node->right) Q.push(node->right);
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }
};
 

复杂度分析

时间复杂度：O(n)，其中 n 为二叉树的节点个数。与方法一同样的分析，每个节点只会被访问一次。

空间复杂度：此方法空间的消耗取决于队列存储的元素数量，其在最坏情况下会达到 O(n)。

三，对称二叉树

101. 对称二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/symmetric-tree/?plan=data-structures&plan_progress=ggfacv7

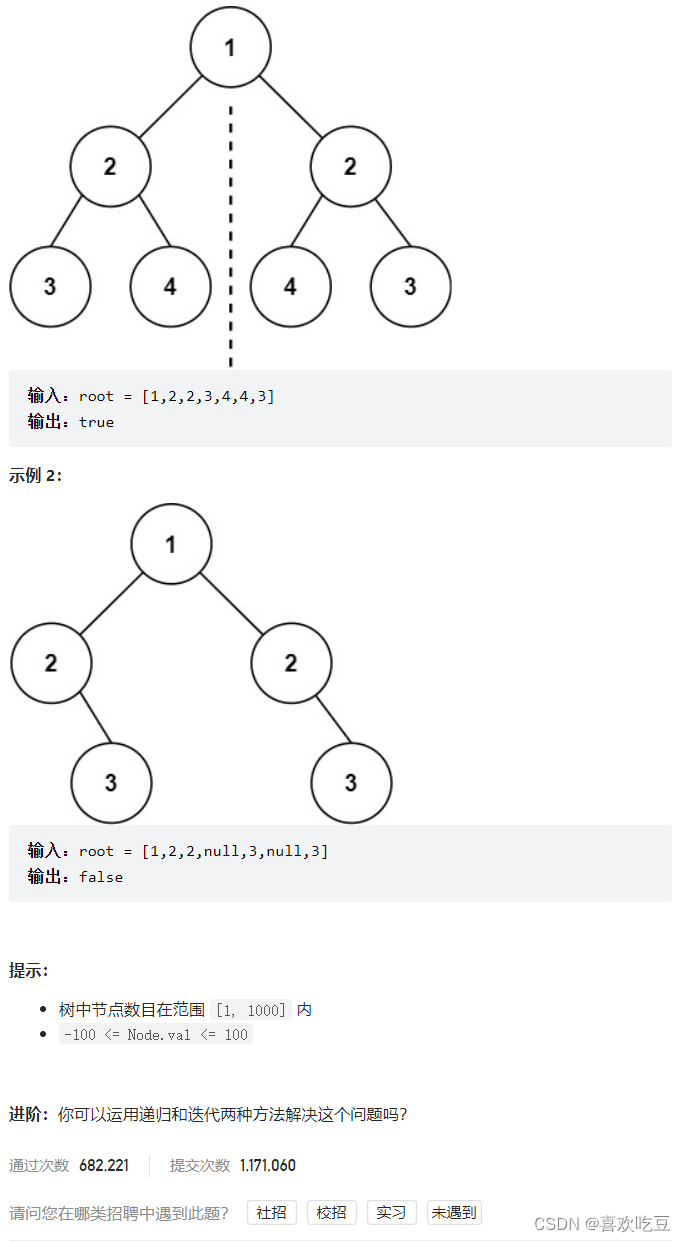
 1，递归

思路和算法

如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

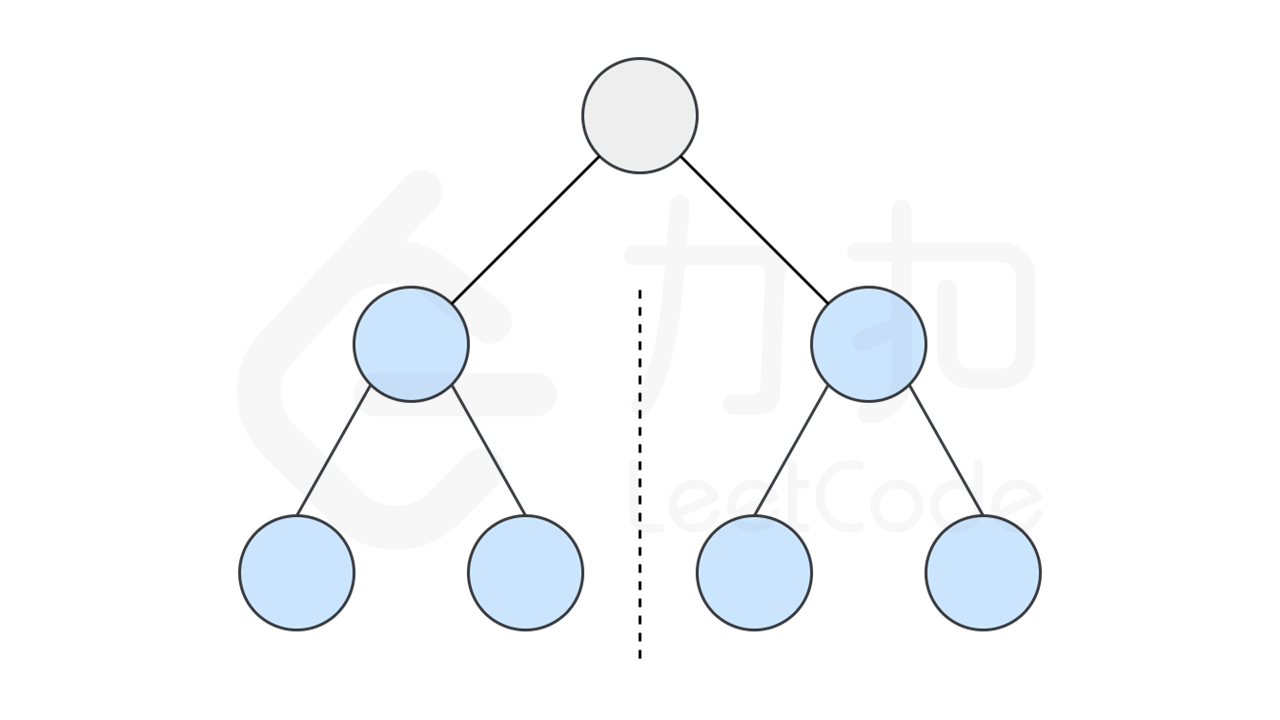
因此，该问题可以转化为：两个树在什么情况下互为镜像？

如果同时满足下面的条件，两个树互为镜像：

它们的两个根结点具有相同的值
每个树的右子树都与另一个树的左子树镜像对称

我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树，p 指针和 q 指针一开始都指向这棵树的根，随后 p 右移时，q 左移，p 左移时，q 右移。每次检查当前 p 和 q 节点的值是否相等，如果相等再判断左右子树是否对称。

class Solution {
public:
    bool check(TreeNode *p, TreeNode *q) {
        if (!p && !q) return true;
        if (!p || !q) return false;
        return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
    }
 
    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};
 

复杂度分析

假设树上一共 n 个节点。

时间复杂度：这里遍历了这棵树，渐进时间复杂度为 O(n)。
空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空间复杂度为O(n)。

2，迭代

思路和算法

「方法一」中我们用递归的方法实现了对称性的判断，那么如何用迭代的方法实现呢？首先我们引入一个队列，这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

class Solution {
public:
    bool check(TreeNode *u, TreeNode *v) {
        queue <TreeNode*> q;
        q.push(u); q.push(v);
        while (!q.empty()) {
            u = q.front(); q.pop();
            v = q.front(); q.pop();
            if (!u && !v) continue;
            if ((!u || !v) || (u->val != v->val)) return false;
 
            q.push(u->left); 
            q.push(v->right);
 
            q.push(u->right); 
            q.push(v->left);
        }
        return true;
    }
 
    bool isSymmetric(TreeNode* root) {
        return check(root, root);
    }
};
 

复杂度分析

时间复杂度：O(n)，同「方法一」。
空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 n 个点，故渐进空间复杂度为 O(n)。