【670. 最大交换】

来源：力扣（LeetCode）

描述：

给定一个非负整数，你至多可以交换一次数字中的任意两位。返回你能得到的最大值。

示例 1 :

输入: 2736
输出: 7236
解释: 交换数字2和数字7。
1
2
3

示例 2 :

输入: 9973
输出: 9973
解释: 不需要交换。
1
2
3

注意:

• 给定数字的范围是 [0, 10⁸]

方法一：直接遍历

由于对于整数 num 的十进制数字位长最长为 8 位，任意两个数字交换一次最多有 28 种不同的交换方法，因此我们可以尝试遍历所有可能的数字交换方法即可，并找到交换后的最大数字即可。(类似选择排序，但是只能交换一次。)

• 我们将数字存储为长度为 n 的列表，其中 n 为整数 num 的十进制位数的长度。对于位置为 (i, j) 的每个候选交换，我们交换数字并记录组成的新数字是否大于当前答案；
• 对于前导零的问题，我们也不需要特殊处理。
• 由于数字只有 8 位，所以我们不必考虑交换后溢出的风险；

代码：

class Solution {
public:
    int maximumSwap(int num) {
        string charArray = to_string(num);
        int n = charArray.size();
        int maxNum = num;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                swap(charArray[i], charArray[j]);
                maxNum = max(maxNum, stoi(charArray));
                swap(charArray[i], charArray[j]);
            }
        }
        return maxNum;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

执行用时：0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗：5.9 MB, 在所有 C++ 提交中击败了10.84%的用户
复杂度分析
时间复杂度：O(log²num)，其中整数 num 为给定的数字。num 转换为十进制数，有 O(lognum) 个数字，一共有 O(log² num) 种不同的交换方法。
空间复杂度：O(lognum)，其中整数 num 为给定的数字。 num 转换为十进制数，有 O(lognum) 个数字，需要保存 num 所有的数字。

方法二：贪心

设整数 num 从右向左的数字分别为(d₀, d₁, d₂, ⋯, d_n−1)，则此时我们可以知道:

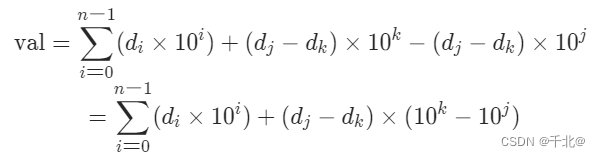
假设我们对位于 j, k 位上的数字进行交换，其中满足 0 ≤ j < k < n，则可以知道交换后的值 val 如下: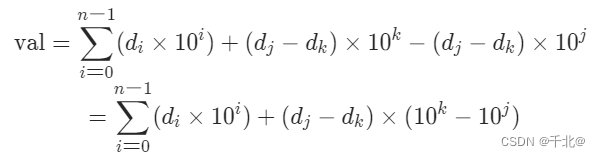

根据以上等式我们可以看出，若使得 \textit{val}val 的值最大，应依次满足如下条件：

• 最优的交换一定需要满足 d_j > d_k ；

• 在满足 d_j > d_k 时，应该保证索引 k 越大从而使得数字 val 越大；

• 在同样大小的数字 d_k 时，应使得数字 d_j 越大从而使得 val 越大；

• 在同样大小的数字 d_j 时，应使得索引 j 越小从而使得 val 越大；

通过以上可以观察到右边越大的数字与左边较小的数字进行交换，这样产生的整数才能保证越大。因此我们可以利用贪心法则，尝试将数字中右边较大的数字与左边较小的数字进行交换，这样即可保证得到的整数值最大。具体做法如下：

• 我们将从右向左扫描数字数组，并记录当前已经扫描过的数字的最大值的索引为 maxId 且保证 maxId 越靠近数字的右侧，此时则说明 charArray[maxId] 则为当前已经扫描过的最大值。

• 如果检测到当前数字 charArray[i] < charArray[maxId]，此时则说明索引 i 的右侧的数字最大值为 charArray[maxId]，此时我们可以尝试将 charArray[i] 与 charArray[maxId] 进行交换即可得到一个比 num 更大的值。我们尝试记录当前可以交换的数对 (i, maxId)，根据贪心法则，此时最左边的 i 构成的可交换的数对进行交换后形成的整数值最大。

代码：

class Solution {
public:
    int maximumSwap(int num) {
        string charArray = to_string(num);
        int n = charArray.size();
        int maxIdx = n - 1;
        int idx1 = -1, idx2 = -1;
        for (int i = n - 1; i >= 0; i--) {
            if (charArray[i] > charArray[maxIdx]) {
                maxIdx = i;
            } else if (charArray[i] < charArray[maxIdx]) {
                idx1 = i;
                idx2 = maxIdx;
            }
        }
        if (idx1 >= 0) {
            swap(charArray[idx1], charArray[idx2]);
            return stoi(charArray);
        } else {
            return num;
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

执行用时：0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗：5.7 MB, 在所有 C++ 提交中击败了81.75%的用户
复杂度分析
时间复杂度：O(lognum)，其中整数 num 为给定的数字。num 转换为十进制数，有 O(lognum) 个数字，需要遍历一次所有的数字即可。
空间复杂度：O(lognum)，其中整数 num 为给定的数字。num 转换为十进制数，有 O(lognum) 个数字，需要保存 num 所有的数字。
author：LeetCode-Solution