-
欧氏距离,曼哈顿距离,闵可夫斯基距离,马氏距离,汉明距离
欧氏距离
欧氏距离( Euclidean distance)是一个通常采用的距离定义,它是在N维空间中两个点之间的真实距离。
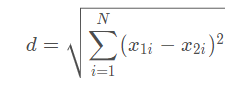
曼哈顿距离
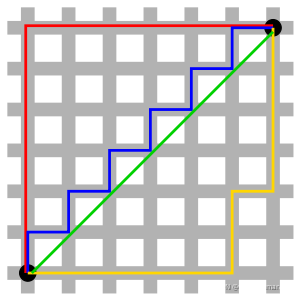
曼哈顿距离是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。
下图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
闵可夫斯基距离
闵可夫斯基距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述,它包含了欧几里得距离(p = 2)和曼哈顿距离(p = 1),就是闵可夫斯基距离的特殊情况:
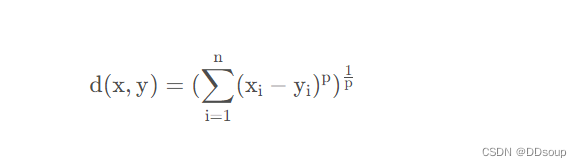
python实现
- def MinkowskiDistance(x, y, p):
- import math
- import numpy as np
- zipped_coordinate = zip(x, y)
- return math.pow(np.sum([math.pow(np.abs(i[0]-i[1]), p) for i in zipped_coordinate]), 1/p)
马氏距离
在介绍马氏距离之前,我们先来看如下几个概念:
方差:方差是标准差的平方,而标准差的意义是数据集中各个点到均值点距离的平均值。反应的是数据的离散程度。
协方差: 标准差与方差是描述一维数据的,当存在多维数据时,我们通常需要知道每个维数的变量中间是否存在关联。协方差就是衡量多维数据集中,变量之间相关性的统计量。比如说,一个人的身高与他的体重的关系,这就需要用协方差来衡量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。
协方差矩阵: 当变量多了,超过两个变量了。那么,就用协方差矩阵来衡量这么多变量之间的相关性。假设 X 是以 n 个随机变数(其中的每个随机变数是也是一个向量,当然是一个行向量)组成的列向量:
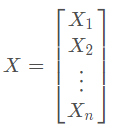
其中,
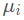 是第i个元素的期望值,即
是第i个元素的期望值,即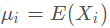 。协方差矩阵的第 i, j 项(第 i, j 项是一个协方差)被定义为如下形式:
。协方差矩阵的第 i, j 项(第 i, j 项是一个协方差)被定义为如下形式: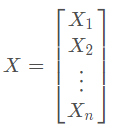
即:
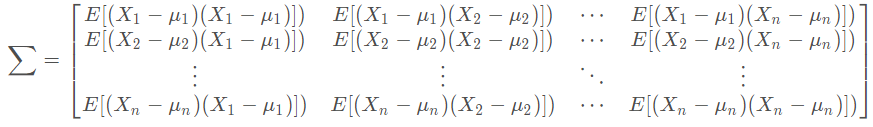
矩阵中的第 ( i , j ) 个元素是
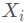 与
与 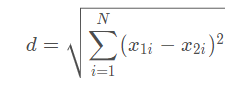 的协方差。
的协方差。马氏距离(Mahalanobis Distance)是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题;可以应对高维线性分布的数据中各维度间非独立同分布的问题。
汉明距离
汉明距离(Hamming Distance)是应用于数据传输差错控制编码的距离度量方式,它表示两个(相同长度)字符串对应位不同的数量。对两个字符串进行异或运算,并统计结果为1的个数,那么这个数就是汉明距离。我们也可以将汉明距离理解为两个等长字符串之间将其中一个变为另外一个所需要作的最小替换次数。
python实现
- def HammingDistance(x, y):
- return sum(x_ch != y_ch for x_ch, y_ch in zip(x, y))
-
相关阅读:
Part2_扩展MATSIM_Subpart13_开发过程和自己的模块_第45章 如何编写自己的扩展并可能将其贡献给Matsim
【Linux】:进程间通信
学习笔记:物理渲染-间接光照
【HuggingFace文档学习】Bert的token分类与句分类
SpringCloud:Nacos注册中心和服务消费方式
Win11如何增强麦克风?Win11增强麦克风的设置
【微服务】spring 控制bean加载顺序使用详解
CSDN21天学习挑战赛之选择排序
50天50个前端小项目(纯html+css+js)第十九天(主题时钟)
Java 转换 WebP 图片,使用 webp-imageio
- 原文地址:https://blog.csdn.net/m0_61897853/article/details/126839902