【43. 数位统计DP（计数问题）】

方法

• 最重要一点：分情况讨论

• 比如说我要找[1,abcdefg]中的数中1出现的个数
  就得先求1在每一个位置上出现的次数

• 比如我要找第4位上出现的1的数有几个
  就是要找满足 1 <= xxx1yyy <= abcdefg

  1. xxx∈[000,abc-1] , yyy∈[000,999] , ans += abc*1000
     //如果前三位没填满，则后三位就可以随便填
  2. xxx == abc , yyy∈?
     if(d < 1) yyy不存在 , ans += 0
     if(d == 1) yyy∈[000,efg] , ans += efg+1
     if(d > 1) yyy∈[000,999] , ans += 1000
     //如果前三位填满了，后三位怎么填取决于当前这一位
     然后每一位上都是这么讨论的，最后累加起来就是总共出现的次数

• 这样就是求出来了[1,n],然后如果我想求[l,r]的用一下前缀和就搞定了

特殊情况（边界问题）

1. x在第1位上出现的次数（不用考虑前半段）：

bcdefg∈[00000,bcdefg] , ans += bcdefg+1
1

2. x在最后一位上出现的次数（不用考虑后半段）：

//不知道为什么y老大没有说这种情况，但是我觉得应该讨论一下的吧
如果g<x，那么不存在这样的数，ans += 0
如果g==x，那么有一个这样的数，ans += 1
如果g>x，yyyyyy∈[000000,abcdef] , ans += abcdef+1
1
2
3
4

3. 如果我们枚举的数是0的话 ：(最复杂)

//恶魔讨论
0不能在第一位 
而且枚举到的这一位前面不能全是0，即
xxx∈[001,abc-1]
1
2
3
4

那当时直播的时候秦淮岸大佬说应该是从100到abc-1
因为我们说“不能有前导零”

正确理解“前导零”：
这个题里面，如果我要找一个数x在[1,n]中出现了几次
这里我们假设n是个五位数
要想找x在[1,n]中的一位数、两位数、三位数、四位数中出现的次数，
都是通过前面有那么一个没有实际作用的前导零来完成的
那么如果我们执着于“不能有前导零”，
则我们找出来的数只可能是个五位数，就不能正确完成了

说到这里，大家应该明白为什么从100到abc-1不对了吧
从100开始的话我们凑出来的数全是五位数啊
所以该有0的时候前面是可以有0的

我们在这里说的没有前导零，
指的是我们枚举x=0在哪一位上时，不考虑0做当前这个数的第一位
举个例子：
如果我们要找[1,1234]中0出现次数
那么首先0不可以做第一位
然后当0做第二位的时候，第一位不能是0
（因为第一位如果是0的话这个数就是00xx，还是不含有0的）
然后0做第三位的时候前两位不能同时为0
（因为前两位都是0那这个数就是000x，还是不含有0）
最后0做第4位的时候前三位不能是000
（因为这样最后这个数就是0，而我们要从[1,1234]中找）

这跟我们故意弄上去几个0当空气是有区别的，在询问0的个数的时候才有这种特殊情况


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

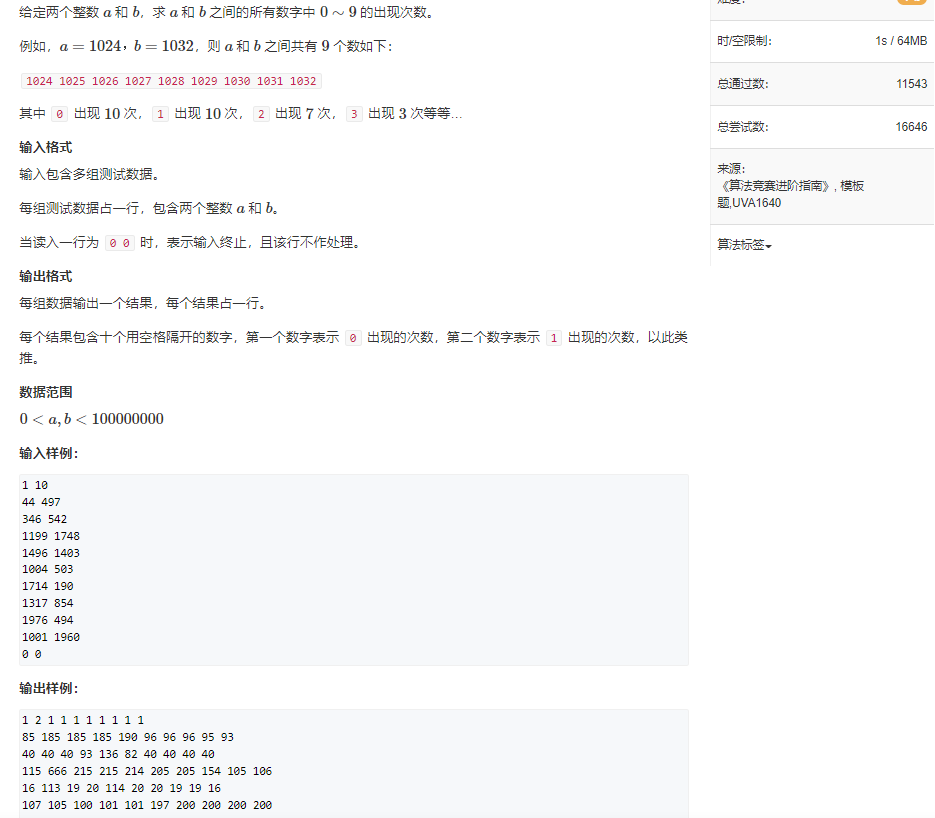
题目

代码

#include 
#include 
#include 
using namespace std;
const int N = 10;

/*

001~abc-1, 999

abc
    1. num[i] < x, 0
    2. num[i] == x, 0~efg
    3. num[i] > x, 0~999

*/
//从枚举的那一位，前面这些位组成的数字是多少
int get(vector<int> num, int l, int r)
{
    int res = 0;
    for (int i = l; i >= r; i -- ) res = res * 10 + num[i];
    return res;
}

int power10(int x)
{
    int res = 1;
    while (x -- ) res *= 10;
    return res;
}


int count(int n, int x)   //从1~n之间统计x的出现的次数
{ 
    if (!n) return 0;     //统计的是1~n之间数字出现的次数，n = 0时一个数也没有
    vector<int> num;
    while (n)            //把n的每一位抠出来
    {
        num.push_back(n % 10);
        n /= 10;
    
    }
    n = num.size();       //n的位数
    
    int res = 0;          //res表示答案  
    
    for (int i = n - 1 - !x; i >= 0; i --)//从最高位开始枚举, -!x就是放最高位（x）等于0时，从第二位开始枚举
    {
        if (i < n - 1)
        {
            res += get(num, n - 1, i + 1) * power10(i);  //第一种情况
            if (!x) res -= power10(i);
        }
        if (num[i] == x) res += get(num, i - 1, 0) + 1;      //第2.2种情况，注意
        else if (num[i] > x) res += power10(i);          //第2.3种情况
    }
    return res;
}


int main()
{
    int a, b;
    while (cin >> a >> b , a||b) //a和b都不等于0
    {
        if (a > b) swap(a, b);

        for (int i = 0; i <= 9; i ++ )
            cout << count(b, i) - count(a - 1, i) << ' ';
        cout << endl;
    }

    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75

借鉴：https://www.acwing.com/solution/content/5623/