树与图的广度优先遍历

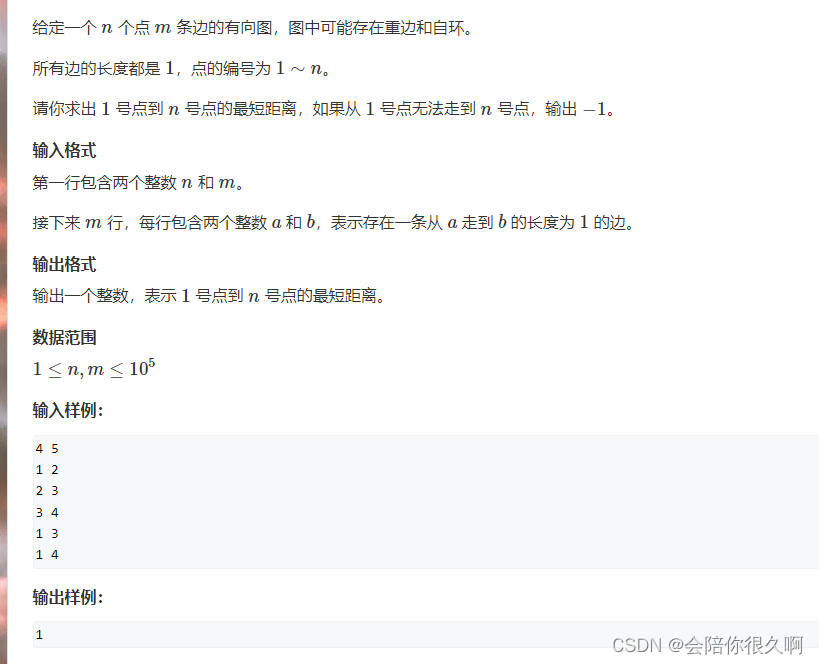
思路：用广度优先搜索的思想，每当队列pop出一个元素时，将于其距离为1的节点都加到队列中（即层次遍历的思想）。

如果对层次遍历的思想有疑问的同学，建议先划到下方，4. 可能有帮助的前置习题，在给出的链接中复习一下层次遍历的思想。

本题最大的难点就在于如何进行层次遍历，我们来看这样一个例子，有这样一幅图，我已经将其转换成了邻接表进行存储。（不知道如何转换成邻接表存储的同学，建议先划到下方，4. 可能有帮助的前置习题，在给出的链接中复习一下如何用邻接表存储图）

我们可以看到，图中的数组是一个存储头结点的数组，我们给定一个节点1，那么在h[1]指向的这条链表上，都是与节点1相邻的节点（即距离为1）；因此，在pop出一个节点t时，只需使用h[t]指向它的链表，再通过for(int i = h[t]; i != -1; i = ne[i])，就可以遍历一整条链表上的节点。然后在遍历时将其加到队列中，并将其的长度置位h[t]+1即可；

上述文字转换成代码如下（d数组用来存储节点1到节点j的距离）：

for (int i = h[t]; i != -1; i = ne[i]) // ne[i]上的点都是与i节点距离为1的点
{
int j = e[i]; // 向外走一步
if (d[j] == -1) // 如果j没有被遍历过
{
d[j] = d[t] + 1; // 因为路径长度都是1，所以直接在上一步的基础上加上1即可
q.push(j); // 将j加到队列中
}
}
3. 解法
---------------------------------------------------解法---------------------------------------------------

#include
#include
#include
#include
#include

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];// 保存1号点到各个点的距离
// -------------------------------A1开始------------------------------------
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// -------------------------------A1结束------------------------------------
int bfs()
{
//---------------------------------------------A2开始-------------------------------
memset(d, -1, sizeof d);

queue q;
d[1] = 0;
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();
    //---------------------------------------A2结束--------------------------------

    // ---------------核心代码开始---------------------------------------
    // 循环遍历所有与t相距为1的节点
    for (int i = h[t]; i != -1; i = ne[i]) // ne[i]上的点都是与i节点距离为1的点
    {
        int j = e[i]; // 向外走一步
        if (d[j] == -1) // 如果j没有被遍历过
        {
            d[j] = d[t] + 1; // 因为路径长度都是1，所以直接在上一步的基础上加上1即可
            q.push(j); // 将j加到队列中
        }
    }
}
return d[n]; // 返回的d[n]即是节点1到节点n的距离

// ---------------核心代码结束---------------------------------------
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

}

// ---------------A3开始---------------------------------------
int main()
{
scanf(“%d%d”, &n, &m);
memset(h, -1, sizeof h);

for (int i = 0; i < m; i ++ )
{
    int a, b;
    scanf("%d%d", &a, &b);
    add(a, b);
}

cout << bfs() << endl;

return 0;
1
2
3
4
5
6
7
8
9
10

}
// ---------------A3结束---------------------------------------
一些注释

我将代码分为了A1、A2、A3和核心代码四块；

• 真正基于本题实现的代码，只有核心代码的6句
• A1和A3代码来自于[AcWing]846. 树的重心（C++实现）树与图的dfs模板题具体指的是邻接表的存储和main函数的输入输出；
• A2块代码来自于 [AcWing]844. 走迷宫（C++实现）bfs的思想 ，其展现了层次遍历的思想以及队列是如何实现该思想的。

4. 可能有帮助的前置习题
   [AcWing]844. 走迷宫（C++实现）bfs的思想 （主要是其中的层次遍历的思想以及其是如何用队列实现的）
   邻接表的存储和main函数的输入输出详见[AcWing]846. 树的重心（C++实现）树与图的dfs模板题
5. 所用到的数据结构与算法思想
   bfs
   队列
6. 总结
   bfs遍历树和图的模板题，主要是层次遍历的思想，其思想简而言之就是当每次pop出队时，将与它距离为1的节点全部加到队列中。推荐熟记全部代码。

判断1号节点能否走到n号节点，广度优先遍历即可。

思路：

用 dist 数组保存1号节点到各个节点的距离，初始时，都是无穷大。

用 st 数组标记各个节点有没有走到过。

从 1 号节点开始，广度优先遍历：

1 号节点入队列，dist[1] 的值更新为 0。

如果队列非空，就取出队头，找到队头节点能到的所有节点。如果队头节点能到走到的节点没有标记过，就将节点的dist值更新为队头的dist值+1，然后入队。

重复步骤 2 直到队列为空。

这个时候，dist数组中就存储了 1 号节点到各个节点的距离了。如果距离是无穷大，则不能到达，输出 -1，如果距离不是无穷大，则能到达，输出距离。

图的存储：邻接表

用 h 数组保存各个节点能到的第一个节点的编号。开始时，h[i] 全部为 -1。

用 e 数组保存节点编号，ne 数组保存 e 数组对应位置的下一个节点所在的索引。

用 idx 保存下一个 e 数组中，可以放入节点位置的索引

插入边使用的头插法，例如插入：a->b。首先把b节点存入e数组，e[idx] = b。然后 b 节点的后继是h[a]，ne[idx] = h[a]。最后，a 的后继更新为 b 节点的编号，h[a] = idx，索引指向下一个可以存储节点的位置，idx ++ 。

#include
#include
#include
#include
using namespace std;

const int N = 100010;

int h[N],ne[N], e[N], idx;//邻接表数据结构
int dist[N];//存储距离
int st[N];//标记点是否走到过
int n, m;

void add(int a, int b)//邻接表存储图
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs()
{
memset(dist, 0x3f, sizeof(dist));//初始都没有走到过，距离无穷大
dist[1] = 0;//从1号节点开始，距离为0
queue q;//队列
q.push(1);//1号节点入队列
st[1] = 1;//1到1的距离为0，已经求出
while(q.size())//对列非空，就一直往后搜索
{
int t = q.front();//队头出队，找该点能到的点
q.pop();
for(int i = h[t]; i != -1; i = ne[i])//遍历所有t节点能到的点，i为节点索引
{
int j = e[i];//通过索引i得到t能到的节点编号
if(!st[j])//如果没有遍历过
{
dist[j] = dist[t] + 1;//距离为t号节点的距离+1
q.push(j);//节点入队
st[j] = 1;//入队后标记，已经遍历过了
}
}
}
}

int main()
{
cin >> n >>m;
memset(h, -1, sizeof h);//初始化，所有节点没有后继，后继都是-1
for(int i = 0; i < m; i++)//读入所有边
{
int a, b;
cin >> a >> b;
add(a, b);//加入邻接表
}
bfs();//广度优先遍历

cout << (dist[n] == 0x3f3f3f3f ? -1 : dist[n]);//如果到n号节点的距离不是无穷大，输出距离，如果是无穷大，输出-1.
return 0;
1
2

}