学习笔记--LinearSVM#Hardmax/softmax

functional margin#函数距离#满足最小距离条件下使最小距离最大化#泛函
r1 = minr = yi(wxi+b)
#为避免出现2r1 = 2yi(wxi+b)#3r1…
进行归一化，转化为几何距离
r = yi(w/||w||xi + b/||w||)=r1/||w||
r2 = minr
最优化问题转变为#
max||w||
实则min(s.t w,b) ||w||#在满足最小距离条件w,b，求min范数||w||的泛函问题，反正最后弄成
min(w,b)2/||w||^2
s.t. yi(wxi+b)-1>=0#集合距离最小条件下把||w||最小#实则在满足函数最小距离解的结合中去找到让||w||最大的解。
bia个图

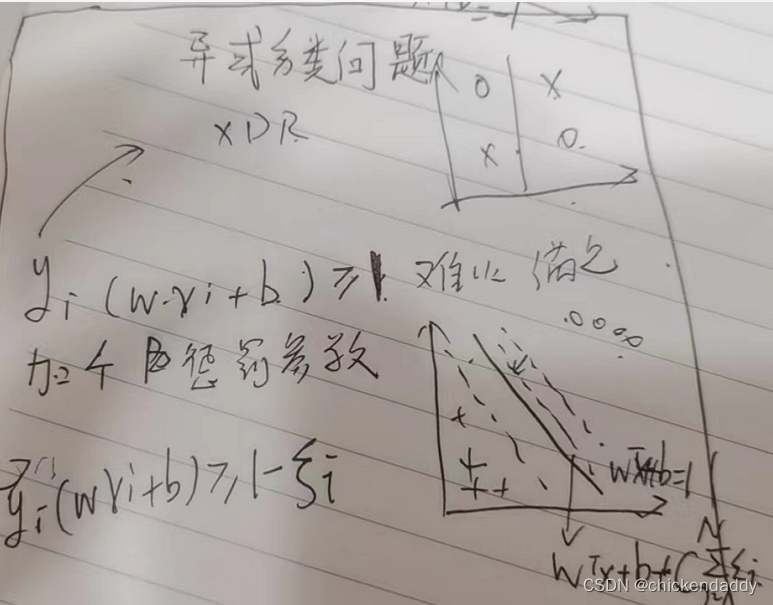
实则yi(wxi+b)>=1，数据点经常难以满足这个条件，所以价格惩罚参数让它变小点：
min(w,b)0.5||w||^2+C(m1+m2+…mn)
yi(wxi+b)>=1-mi