Pytorch学习——梯度下降和反向传播 03 未完

1 梯度是什么

通俗的来说就是学习（参数更新）的方向。
简单理解，（对于低维函数来讲）就是导数（或者是变化最快的方向）

2 判断模型好坏的方法

1. 回归损失
   $$loss=(Y_{predict}-Y_{true}{)}^2$$

2. 分类损失

$$loss=Y_{true}\cdot log(Y_{predict})$$

3 前向传播

$J(a,b,c)=3(a+bc)$， 令$u=a+v$，$v=bc$，把它绘制成计算图可以表示为：

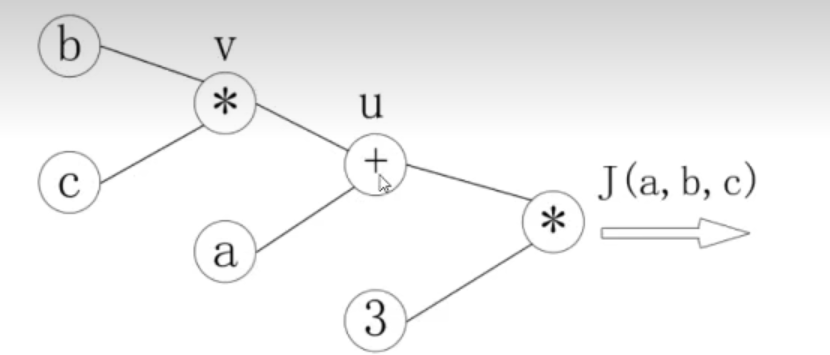
绘制成计算图之后，可以清楚的看到前向计算的过程。

4 反向传播

对每个节点求偏导可以有：

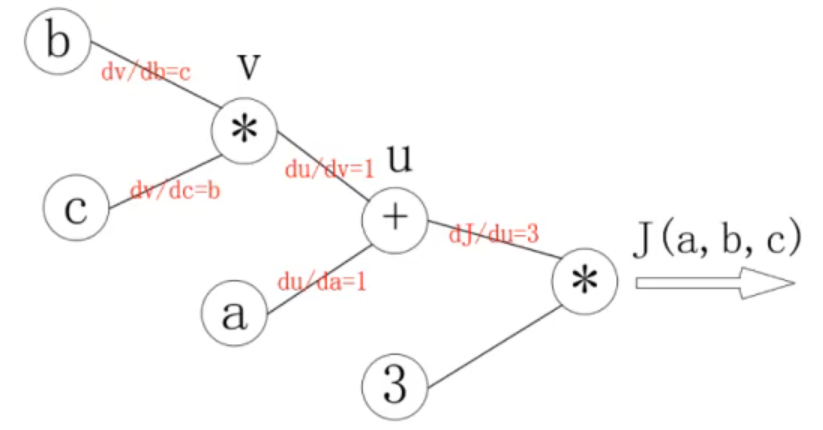
反向传播就是一个从右到左的过程，自变量$a,b,c$各自的骗到就是连线上梯度的乘积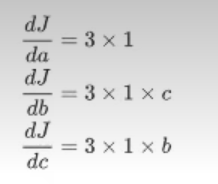

5 Pytorch中反向传播和梯度计算的方法

5.1 前向计算

对于Pytorch中的一个tensor，如果设置它的属性， .require_grad=True ，那么会追踪对于该张量的所有操作。
默认值为None

import torch

x = torch.ones(2, 2, requires_grad=True)
print(x)

y = x+2
print(y)

z = y*y*3
print(z)
1
2
3
4
5
6
7
8
9
10

输出：

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)
tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>)
1
2
3
4
5
6

总结：

（1）之后的每次计算都会修改其grad_fn属性，用来记录做过的操作；
（2）通过这个函数和grad_fn 可以生成计算图。

---

• 注意

为了防止跟踪历史记录，可以将代码包装在with torch.no_grad 中。表示不需要追中这一块的计算。

import torch

x = torch.ones(2, 2, requires_grad=True)
print(x)

y = x+2
print(y)

z = y*y*3
print(z)

with torch.no_grad():
    u = x+y+z

print(u)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)
tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>)
tensor([[31., 31.],
        [31., 31.]])
1
2
3
4
5
6
7
8

5.2 梯度计算

可以使用backward() 方法来进行反向传播，计算梯度 out.backward() ，此时能方便求出导数。

调用x.grad() 可以获取导数值。

注意：
在输入是一个标量的情况下，可以调用输出tensor的backward()方法，但是在输出是一个向量的时候，调用backward时要传入其他参数。

---

5.3 torch.data

当tensor的require_grad 为false的时候，a.data 等同于 a

当tensor的require_grad 为True的时候，a.data 表示仅仅获取其中的数据

---

5.4 tensor.numpy

require_grad=True 不能够直接转换，需要用torch.detach().numpy()

detach相当于是深拷贝
相当于把原来的tensor数据“抽离”出来，并部影响原来的tensor，然后进行深拷贝，转化为numpy数据。