C++实现并查集

并查集原理

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。

1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数，负号代表根，数字代表该集合中元素个数
3. 数组中如果为非负数，代表该元素双亲在数组中的下标

并查集一般可以解决以下问题：

1. 查找元素属于哪个集合
   沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置）
2. 查看两个元素是否属于同一个集合
   沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
3. 将两个集合归并成一个集合
   将两个集合中的元素合并
   将一个集合名称改成另一个集合的名称
4. 集合的个数
   遍历数组，数组中元素为负数的个数即为集合的个数

并查集实现

class UnionFindSet{
private:
	vector<int> _ufs;
public:
	UnionFindSet(size_t n)
		:_ufs(n, -1)
	{}
	
	int FindRoot(int x)
	{
		int root = x;
		while(_ufs[root] >= 0)
		{
			root = _ufs[x];
		}
		
		//路径压缩
		while(_ufs[x] >= 0)
		{
			int parent = _ufs[x]; //记录下x的父亲节点
			_ufs[x] = root;
			
			x = parent;
		}
		
		return root;
	}	
	
	void Union(int x1, int x2)
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		if(root1 == root2)
			return;
		
		//数据量小的往数据量大的合并
		if(abs(_ufs[root1]) < abs(_ufs[root2])
			swap(root1, root2);
			
		_ufs[root1] += _ufs[root2];
		_ufs[root2] = root1;
	}
	
	bool InSet(int x1, int x2)
	{
		return FindRoot(x1) == FindRoot(x2);
	}
	
	//集合的数量
	size_t SetSize()
	{
		size_t size = 0;
		for(size_t i = 0; i < _ufs.size(); i++)
		{
			if(_ufs[i] < 0)
			{
				++size;
			}
		}	
		
		return size;
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

路径压缩

如果遇到类似以下情况，访问的效率不高，可以在find的同时，把这个节点尽量往上挪一下，减少树的层数，这个过程就叫做路径压缩

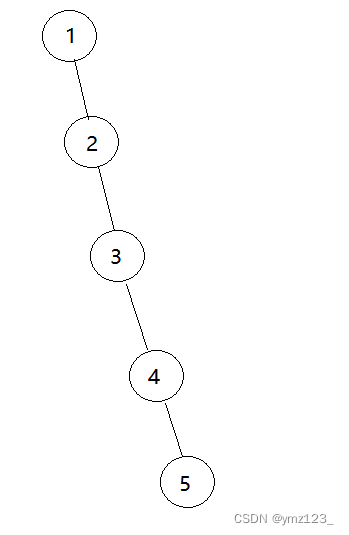
比如查找3，将会压缩成下图：

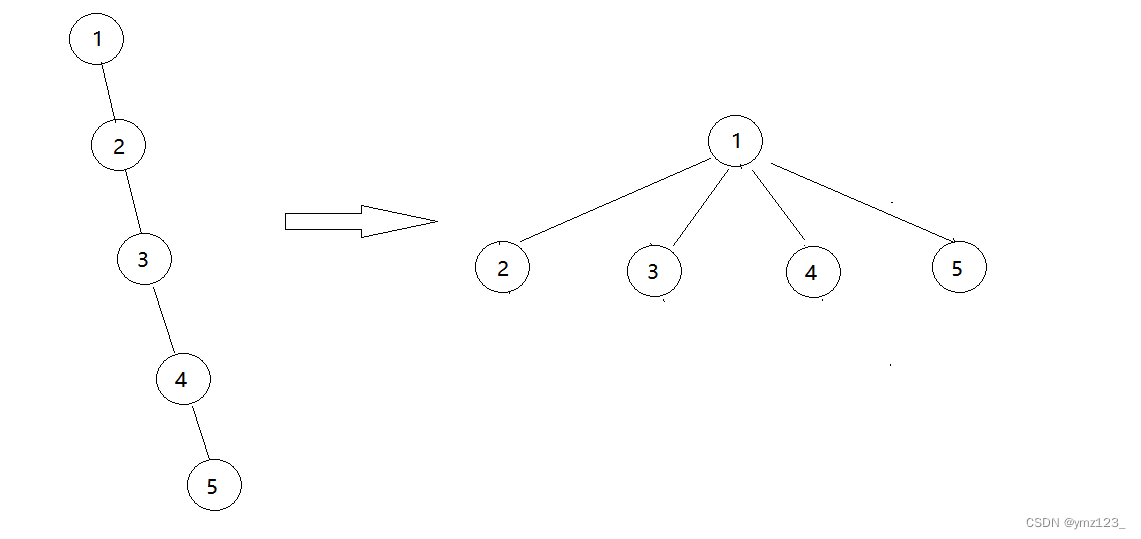
并查集应用

leetcode 116. 省份数量

class Solution {
public:
    int findCircleNum(vector<vector<int>>& isConnected) {
        vector<int> ufs(isConnected.size(), -1);
        auto FindRoot = [&ufs](int x){
            while(ufs[x] >= 0){
                x = ufs[x];
            }
            return x;
        };
        for(int i = 0; i < isConnected.size(); i++){
            for(int j = 0; j < isConnected.size(); j++){
                if(isConnected[i][j] == 1){
                    int root1 = FindRoot(i);
                    int root2 = FindRoot(j);
                    if(root1 != root2){
                        ufs[root1] += ufs[root2];
                        ufs[root2] = root1;
                    }
                }
            }
        }
        int res = 0;
        for(auto e : ufs){
            if(e < 0){
                res++;
            }
        }

        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32