• 算法学习笔记 - 网络流初步

    前言

    网络流是图论中一个博大精深的分支。本篇博客只希望让大家建立对网络流的初步认识，内容会比较浅显。

    一个网络 G = (V, E) 是一张有向图，图中每条有向边 (x, y)∈E 都有一个给定的权值 c(x, y)，称为边的容量。特别地，若 (x, y) 不属于 E，则 c(x, y) = 0。图中还有两个指定的特殊节点 S∈V 和 T∈V(S≠T)，分别称为源点和汇点。

    设 f(x, y) 是定义在节点二元组 (x∈V, y∈V) 上的实数函数，且满足：

    1. f(x, y) ≤ c(x, y)

    2. f(x, y) = - f(y, x)

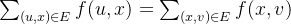
    3. 任意x≠S，x≠T, \sum_{(u, x)\in E}f(u, x)=\sum_{(x,v)\in E}f(x,v)

    f 称为网络的流函数。对于 (x, y)∈ E，f(x, y) 称为边的流量，c(x, y) - f(x, y) 称为边的剩余容量。

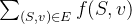    \sum_{(S,v)\in E} f(S,v)称为整个网络的流量（其中 S 表示源点）。

    如下图所示。左边是一个网络，有源点 S、汇点 T 以及 A~E 共 7 个点。有向边上的数值标识了边的容量，例如 c(A, B) = 5。

     右边画出了该网络的一个流，在有向边上用 “f(x, y)/c(x, y)” 的形式标注流量，例如 f(A, B) = 4。流量为 0 的边省略了标注。值得一提的是，按照流函数的定义，图中标注的每条边的反向边其实都有一个负的流量，例如 c(B, A) = 0，f(B, A) = -4，这些没有标出，请读者留意。 

    上文给出的流函数 f(x, y) 的三条性质分别称为容量限制，斜对称和流量守恒。尤其是流量守恒定律，他告诉我们网络中除源点、汇点以外，任何节点不储存流，其流入总量等于流出总量。网络流模型可以形象地描述为：在不超过容量限制的前提下，“流”从源点源源不断地产生，流经整个网络，最终全部归于汇点。

    最大流

    洛谷【模板】网络最大流

    对于一个给定的网络，合法的流函数 f 有很多。其中使得整个网络的流量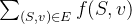\sum_{(S,v)\in E} f(S,v)（其中 S 表示源点）的流函数被称为网络的最大流，此时的流量被称为网络的最大流量。

    最大流能解决许多实际的问题。就拿我们上两节讨论的二分图为例。对于一张 n 个点 m 条边的二分图，我们可以新增一个源点 S 和 一个汇点 T，从 S 到每个左部点连有向边，从每个右部点到 T 连有向边，把原二分图的每条边看作从左部点到右部点的有向边，形成一张 n+2 个点 n+m 条边的网络，网络中每条边的容量都设为 1，如下图所示。容易发现，二分图的最大匹配就等于网络的最大流量，求出最大流后，所有有“流”经过的点、边就是匹配点、匹配边。

    进一步地，若要求二分图多重匹配，则只需把 S 到左部点的有向边容量设为左部点的匹配数量上限 kli，右部点到 T 的有向边容量设为右部点的匹配数量上限 kri，原二分图每条边的容量设为 1，再求最大流即可。

    Edmonds - Karp 增广路算法

    若一条从源点 S 到汇点 T 的路径上各条边的剩余容量都大于 0，则称这条路径为一条增广路。显然，可以让一股流沿着增广路从 S 流到 T，使网络的流量增大。 Edmonds - Karp 算法的思路就是不断用 BFS 寻找增广路，直至网络上不存在增广路为止。

    在每轮寻找增广路的过程中，Edmonds - Karp 算法只考虑图中所有 f(x, y) ＜c(x, y) 的边，用 BFS 找到任意一条从 S 到 T 的路径，同时计算出路径上各边的剩余容量的最小值 minf，则网络的流量就可以增加 minf。

    需要注意的是，当一条边的流量 f(x, y) ＞ 0 时，根据斜对称性质，它的反向边流量 f(x, y) ＜ 0，此时必定有 f(y, x) ＜ c(y, x)。故 Edmonds - Karp 算法在 BFS 时除了原图的边集 E 之外，还应该考虑遍历 E 中每条边的反向边。

    在具体实现时，我们可以按照邻接表“成对存储”技巧，把网络的每条有向边及其反向边存在邻接表下称为 “2 和 3” “4 和 5” “6 和 7”...的位置上，每条边只记录剩余容量 c - f 即可。当一条边 (x, y) 流过大小为 e 的流时，令 (x, y) 的剩余容量减小 e，(y, x) 的剩余容量增大 e。

    如下图所示。第一幅图是网络中每条边的原始容量，Edmonds - Karp 算法找到了流量为 5 的增广路 S→C→D→B→T。于是在第二幅图中，剩余容量对应发生了变化。紧接着，第三幅图中，算法又找到了流量为 2 的增广路 S→A→B→D→E→T。最终在第四幅图中，网络不存在增广路，最大流的大小就是 7。图中省略了剩余容量为 0 的边。

    Edmonds - Karp 增广路算法的时间复杂度 O(nm^2)。然而在实际运用中则远远达不到这个上界，效率较高，一般能够处理 10^3~10^4 规模的网络。

    代码示例

    1. /*
    2. 网络最大流
    3. 采用 Edmonds - Karp 增广路算法
    4. */
    5.  
    6. #include
    7. #include
    8. #include
    9. #include
    10. #include
    11. #include
    12. using namespace std;
    13.  
    14. #define int long long
    15.  
    16. const int maxn = 1001000;
    17. int n, m, s, t;
    18. int tot;
    19. int maxflow;
    20. int head[maxn];
    21. int vis[maxn];
    22. int dis[maxn];
    23. int flow[maxn];
    24. int last[maxn];
    25.  
    26. queue<int> q;
    27.  
    28. struct edge{
    29.     int to;
    30.     int nxt;
    31.     int from;
    32.     int val;
    33. }e[2*maxn];
    34.  
    35. void add(int x, int y, int z){
    36.     tot++;
    37.     e[tot].to = y;
    38.     e[tot].from = x;
    39.     e[tot].val = z;
    40.     e[tot].nxt = head[x];
    41.     head[x] = tot;
    42. }
    43.  
    44. bool bfs(int S, int T){
    45.     for(int i = 1; i <= n; i++) last[i] = vis[i] = -1;
    46.     q.push(S);
    47.     dis[S] = 0;
    48.     vis[S] = 1;
    49.     flow[S] = 0x3f3f3f3f; // 增广路上各边的最小剩余容量
    50.     while(!q.empty()){
    51.         int u = q.front();
    52.         q.pop();
    53.         vis[u] = 0;
    54.         for(int i = head[u]; i; i = e[i].nxt){
    55.             int v = e[i].to;
    56.             if(vis[v] == -1 && e[i].val){
    57.                 flow[v] = min(flow[u], e[i].val);
    58.                 last[v] = i; // 记录前驱，便于找到最长路的实际方案
    59.                 q.push(v);
    60.                 vis[v] = 0;
    61.             }
    62.         }
    63.     }
    64.     if(vis[T] != -1) return 1;
    65.     return 0;
    66. }
    67.  
    68. void update(int S, int T){ // 更新增广路及其反向边剩余容量
    69.     int now = T;
    70.     while(now != S){
    71.         int i = last[now];
    72.         e[i].val -= flow[T];
    73.         e[i ^ 1].val += flow[T]; // 利用“成对存储”的 xor 1 技巧
    74.         now = e[i].from;
    75.     }
    76.     maxflow += flow[T];
    77. }
    78.  
    79. signed main(){
    80.     tot = 1;
    81.     cin >> n >> m >> s >> t;
    82.     for(int i = 1; i <= m; i++){
    83.         int x, y, z;
    84.         cin >> x >> y >> z;
    85.         add(x, y, z);
    86.         add(y, x, 0);
    87.     }
    88.     maxflow = 0;
    89.     while(bfs(s, t)) update(s, t);
    90.     cout << maxflow << endl;
    91.     return 0;
    92. }

    Dinic 算法

    在任意时刻，网络中所有节点以及剩余容量大于 0 的边构成的子图被称为残量网络。Edmonds - Karp 每轮可能会遍历整个残量网络，但只找出 1 条增广路，还有进一步优化的空间。

    之前我们应该就了解过节点的层次 d[x]，它表示 S 到 x 最少需要经过的边数。在残量网络中，满足 d[y] = d[x] + 1 的边 (x, y) 构成的子图被称为分层图。分层图显然是一张有向无环图。

    Dinic 算法不断重复以下步骤，直到在残量网络中 S 不能到达 T：

    1. 在残量网络上 BFS 求出节点的层次，构造分层图。

    2. 在分层图上 DFS 寻找增广路，在回溯时实时更新剩余容量。另外，每个点可以流向多条出边，同时还加入了若干剪枝。

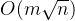
    Dinic 算法的时间复杂度为 O(mn^2)。实际运用中远远达不到这个上界，可以说是比较容易实现的效率最高的网络流算法之一，一般能够处理 10^4~10^5 规模的网络。特别地，Dinic 算法求解二分图最大匹配的时间复杂度为 O(m\sqrt{n})

    代码示例

    1. /*
    2. 网络最大流
    3. 采用 Dinic 算法
    4. */
    5.  
    6. #include
    7. #include
    8. #include
    9. #include
    10. #include
    11. #include
    12. using namespace std;
    13.  
    14. #define int long long
    15.  
    16. const int maxn = 1000100;
    17. int n, m, s, t;
    18. int tot;
    19. int maxflow;
    20. int head[maxn];
    21. int dis[maxn];
    22.  
    23. queue<int> q;
    24.  
    25. struct edge{
    26.     int from;
    27.     int to;
    28.     int nxt;
    29.     int val;
    30. }e[2*maxn];
    31.  
    32. void add(int x, int y, int z){
    33.     tot++;
    34.     e[tot].from = x;
    35.     e[tot].to = y;
    36.     e[tot].val = z;
    37.     e[tot].nxt = head[x];
    38.     head[x] = tot;
    39. }
    40.  
    41. bool bfs(){ // 在残量网络上构造分层图
    42.     memset(dis, 0, sizeof(dis));
    43.     while(!q.empty()) q.pop();
    44.     q.push(s);
    45.     dis[s] = 1;
    46.     while(!q.empty()){
    47.         int x = q.front();
    48.         q.pop();
    49.         for(int i = head[x]; i; i = e[i].nxt){
    50.             int y = e[i].to;
    51.             if(!dis[y] && e[i].val){
    52.                 q.push(y);
    53.                 dis[y] = dis[x] + 1;
    54.                 if(y == t) return 1; 
    55.             }
    56.         }
    57.     }
    58.     return 0;
    59. }
    60.  
    61. int dinic(int x, int flow){ // 在当前分层图上增广
    62.     if(x == t) return flow;
    63.     int rest = flow;
    64.     int k;
    65.     for(int i = head[x]; i && rest; i = e[i].nxt){
    66.         int y = e[i].to;
    67.         if(dis[y] == dis[x] + 1 && e[i].val){
    68.             k = dinic(y, min(rest, e[i].val));
    69.             if(!k) dis[y] = 0; // 剪枝，去掉增广完毕的点
    70.             e[i].val -= k;
    71.             e[i ^ 1].val += k;
    72.             rest -= k;
    73.         }
    74.     }
    75.     return flow - rest;
    76. }
    77.  
    78. signed main(){
    79.     cin >> n >> m >> s >> t;
    80.     tot = 1;
    81.     int x, y, z;
    82.     for(int i = 1; i <= m; i++){
    83.         cin >> x >> y >> z;
    84.         add(x, y, z);
    85.         add(y, x, 0);
    86.     }
    87.     int flow = 0;
    88.     while(bfs()) while(flow = dinic(s, 0x3f3f3f)) maxflow += flow;
    89.     cout << maxflow << endl;
    90.     system("pause");
    91. }

    二分图最大匹配的必须边与可行边

    给定一张二分图，其最大匹配的方案不一定是唯一的。若任何一个最大匹配方案的匹配边都包括 (x, y)，则称 (x, y) 为二分图最大匹配的必须边。若 (x, y) 至少属于一个最大匹配的方案，则称 (x, y) 为二分图最大匹配的可行边。

    先来考虑一种简化情况——二分图的最大匹配是一组完备匹配。我们先任意求出一组完备匹配的方案，此时左，右部所有的节点都是匹配点。

    根据定义，(x, y) 是必须边，当且仅当以下两个条件都满足：

    1. (x, y) 当前是匹配边。

    2. 删除边 (x, y) 后，不能找到另一条从 x 到 y 的增广路。

    (x, y) 是可行边，当且仅当满足以下两个条件之一：

    1. (x, y) 当前是匹配边。

    2. (x, y) 是非匹配边，设当前 x 与 v 匹配，y 与 u 匹配，连接边 (x, y) 后，节点 u，v 失去匹配。必须能找到一条从 x 到 y 的路径。

    考虑必须边的条件，(x, y) 是匹配边，对应 G1 中有一条从 y 到 x 的有向边。在此前提下，若 x 到 y 还存在一条路径，则 x 和 y 互相可达，必处于同一个强连通分量中。如下图所示。， 和 y 在 G1 中互相可达，构成一个环，把环上的边的匹配状态取反，得到另一组完备匹配。

     因此，必须边的判定条件可改写为：(x, y) 当前是二分图 G 的匹配边，并且 x，y 两点在有向图 G1 中属于不同的强连通分量。

    类似地，可行边的判定条件可改写为：(x, y) 当前是二分图 G 的匹配边，或者 x，y 两点在有向图G1 中属于同一个强连通分量。

    在一般的二分图中（最大匹配不一定是完备匹配），可以用最大流计算出任意一组最大匹配。此时必须边的判定条件为：(x, y) 流量为 1，并且在残量网络上属于不同的强连通分量。可行边的判定条件为：(x, y) 流量为 1，或者在残量网络上属于同一个强连通分量。

    最小割

    给定一个网络 G = (V, E)，源点为 S，汇点为 T。若一个边集 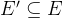E'\subseteq E 被删去之后，源点 S 和汇点 T 不再连通，则称该边集为网络的割。边的容量之和最小的割称为网络的最小割。

    最大流最小割定理

    任何一个网络的最大流量等于最小割中边的容量之和，简记为 “最大流 = 最小割”。

    假设 “最小割 ＜ 最大流”，那么割去这些边之后，因为网络流量尚未最大化，所以仍然可以找到一条 S 到 T 的增广路，与 S,T 不连通矛盾，故 “最小割 ≥ 最大流”。如果我们能给出一个 “最小割 = 最大流”的构造方案，即可得到上述定理。

    求出最大流后，从源点开始沿残量网络 BFS，标记能够到达的点。E 中所有连接 “已标记点 x” 和 “未标记点y” 的边 (x, y) 构成该网络的最小割。

    费用流

    给定一个网络 G = (V, E)，每条边 (x, y) 除了有容量限制 c(x, y)，还有一个给定的 “单位费用” w(x, y) 的流量为 f(x, y) 时，就要花费 f(x, y) * w(x, y)。该网络中总花费最小的最大流被称为 “最小费用最大流”，总花费最大的最大流被称为 “最大费用最大流”，二者合称为 “费用流” 模型。注意：费用流的前提是最大流，然后才考虑费用的最值。

    Edmonds - Karp 增广路算法

    在 Edmonds - Karp 求解最大流的基础上，把 “用 BFS 寻找任意一条增广路” 改为 “用 SPFA 寻找一条单位费用之和最小的增广路” (也就是把 w(x, y) 当作边权，在残量网络上求最短路) 即可求出最小费用最大流。注意：一条反向边 (y, x) 的费用应设为 - w(x, y)。

  • 相关阅读:
    mysql中find_in_set()函数的使用及in()用法详解
    C++ day4
    python 变量引用，值变量
    【web-避开客户端控件】（2.3.4）收集使用数据：反编译浏览器扩展
    Web自动化框架中验证码识别处理全攻略，让测试更得心应手！
    用java代码实现security
    RabbitMQ官方案例学习记录
    【JAVA】快速排序
    【Solution】一文学会微信扫码登录
    关于Go中两个模块互相调用的场景解决方案
  • 原文地址：https://blog.csdn.net/haobowen/article/details/126806848