-
基于 attention 机制的 LSTM 神经网络 超短期负荷预测方法学习记录
LSTM(long short-term memory)长短期记忆
模型基础介绍
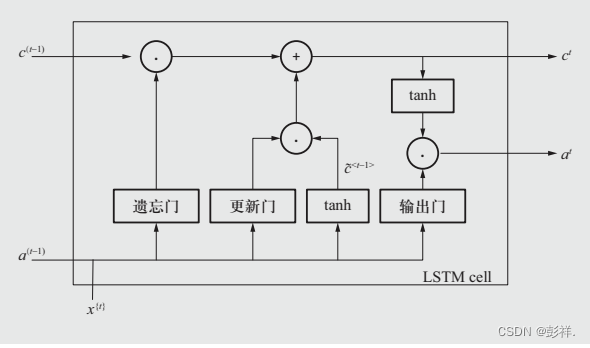
在标准LSTM体系结构中,有1个记忆单元状态和3个门,即更新门Γu、遗忘门Γf和输出门Γo,标准LSTM的体系结构如图2所示。采用X1
, X2 , …, XT 表示LSTM网络中的典型输入序列,则其中 X{t} 表示时间 t
时的输入特征。为了实现重要信息长时间存储,在LSTM的整个周期内设立并维护一个记忆单元c。根据前一时间的激活单元at–1和当前时间的输入
Xt ,通过3个门确定更新、维护或遗忘内部状态向量的具体元素。


标准LSTM网络采用编码器—解码器(encode-decode)结构,将输入序列编码成固定长度的向量表示。当输入序列长度较短时,有较好的学习效果,但当输入序列长度较长时,容易造成信息丢失,难以学到输入序列合理的向量表示。
优势
相较于传统的RNN,其克服了存在的梯度消失和梯度爆炸问题。
不足
LSTM网络的预测效果远优于RNN。然而LSTM网络是将所有输入特征编码成固定长度的向量表示,忽视了其与待预测负荷之间的关联性大小,因而无法有侧重地对历史数据加以利用。
改进
本文针对LSTM算法存在的不足,提出一种基于attention机制的LSTM神经网络。
实验过程
实验主要需确定网络的输入输出变量、数据预处理方法、网络结构、模型训练方法以及网络评价指标。
输入输出变量的确定
确定网络的输入输出变量是确定网络结构的基础。假定负荷采样频率为每小时1次,可获得的网络训练数据集为每天24h的历史负荷数据,为提高网络的预测效果及处理效率,需选择合理的阶数。因负荷值具有一定的随机性,可采用计算样本自相关系数的方法来确定输入变量时间序列的阶数。各阶自相关系数反映了各滞时状态间的相关关系,可反映序列的周期规律。时间序列h阶自相关系数的计 算公式为:

简要而言,即我们不能确定哪个时间段与我们当前时间的关系最为密切,故采用自相关系数计算来确定。通过找到自相关系数衰减为0的阶数,可确定采用 特定时段的历史负荷数据,进行超短期负荷预测,实现
负荷历史数据的充分利用。绘制得到负荷历史数据集的 自相关系数如图3所示。由图可以看出,当阶数取168
时,自相关系数衰减为0,即预测点负荷值只与预测时 刻前168 h的负荷相关,因而输入变量选为预测时刻前 168 h的负荷数据。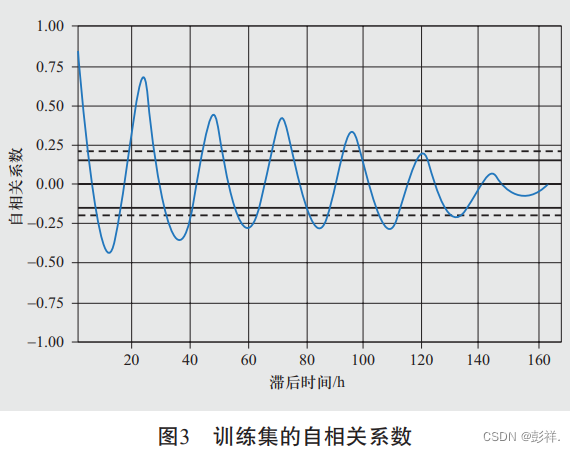
此外,本文目的是预测未来某天某整点时刻的负荷值,则输出变量选为预测点的负荷预测结果。输入数据预处理
数据采集过程中,存在设备故障、人为操作失误等情况,可能会得到偏差较大 的数据或空数据,因而可进行坏数据辨别及修正,降低个别偏差较大、分布稀疏的坏数据对预测准确度的影响。
那么主要便分为坏数据辨别,坏数据修正,归一化三个步骤数据归一化。为方便后续处理,对完成修正的负荷数据进行归一化处理,将负荷数据集矩阵各元素取
值转换在[0,1]内。归一化公式为:
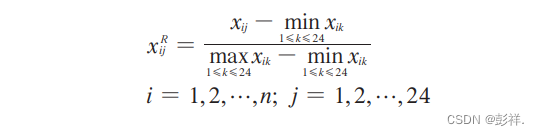
基于attention机制的LSTM网络结构设计
attention机制模拟人脑注意力模型,其主要思想是针对输入序列中影响输出结果的关键部分分配较多的注意力,以更好地学习输入序列中的信息。本文将attention机制作为2个LSTM网络的接口,首先通过一个LSTM网络处理输入序列,实现高层次的特征学习;随后通过合理分配注意力权重,实现记忆单元求解;最后通过再运行一个LSTM网络实现超短期负荷预测。模型展示
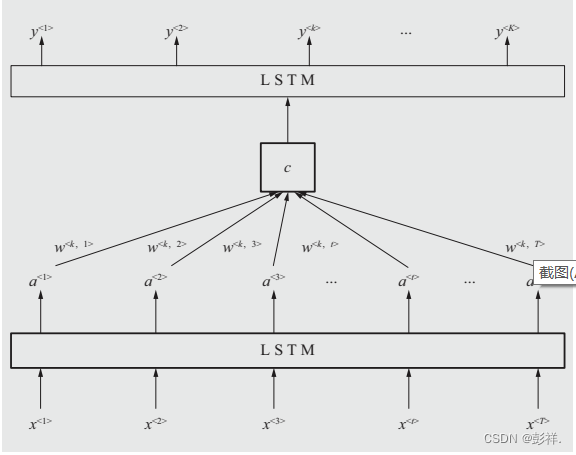
这是一个Seq2Seq模型,即编码器-解码器模型。


模型训练方法
损失函数
均方误差(mean squared error,MSE)用于反映估计量与被估计量之间的差异程度,将其作为本网络的目标损失函数,其计算公式为:
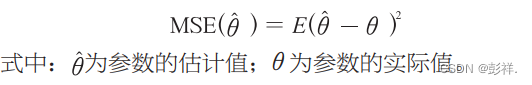
优化器
选用Adam算法替代传统随机梯度下降过程,基于训练数据和损失函数计算各参数的一阶矩估计及二阶矩估计,并针对计算结果动态调整每个参数的学习速率,实现网络权重的迭代更新。训练过程采用学习速度(learning rate,Ir)呈指数规律下降的方式,实现训练后期最优解的确定。经多次训练后,选取最佳优化结果。
关于Adam
Adam 是一种可以替代传统随机梯度下降(SGD)过程的一阶优化算法,它能基于训练数据迭代地更新神经网络权重。
Adam介绍网络评价指标
平均绝对百分误差(mean absolute percentage error,MAPE)是一种常用于衡量预测准确性的指标。本文通过该指标对网络的负荷预测结果做出评判,其计算公式为:
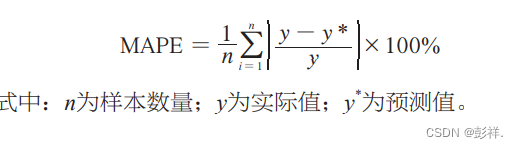
之后,该模型与标准BP网络相对比,在性能上有了明显提升。 -
相关阅读:
微信每日早安推送 Windows版
leetcode 图相关的题
FPGA上板项目(一)——点灯熟悉完整开发流程、ILA在线调试
Redis.
C Primer Plus(6) 中文版 第6章 C控制语句:循环 6.11 数组简介
Ngnix优化
MySQL 事务隔离级别和MVCC版本控制
若依 vue前端 动态设置路由path不同参数 在页面容器里打开新页面,面包屑和标签页标题根据参数动态改变
慕思股份深交所上市:靠床垫和“洋老头”走红 市值224亿
幻兽帕鲁服务器多少钱?有买过的吗?
- 原文地址:https://blog.csdn.net/pengxiang1998/article/details/126817696