• NFA转换成DFA的方法——子集法

    承接上文在上一篇文章中说了

    DFA 是 NFA 的特例 对于每个NFA M 存在一个DFA M” 使得 L(M)=L(M”)
    NFA缺点： 其不确定性使得识别单词符号的速度较慢
    DFA缺点： 占用空间太大
    NFA到DFA的变换
    子集构造法
    DFA的一个状态是NFA的一个状态集合
    子集法相关的三个运算
    (1) 状态 q 的 ε 闭包： ε-closure(q) 从状态 q 出发，只经 ε 转换能到 达的所有状态的集合
    (a) q ∈ ε-closure(q) ；
    (b) 从 q 出发经任意条 ε 弧而能到达的任何状态 q‟ ∈ ε- closure(q)
    (2) 状态集合 I 的 ε 闭包： ε-closure(I)
    {q‟|q‟ ∈ ε-closure(q) & q ∈ I}
    (3) I a =ε-closure(J) a ∈ ∑ ，其中 J 为从 I 中任一状态出发经 输入符号 a( 可先经过 ε) 所能到达状态结点的全体。
    Ia是 状态集I 的 a 弧转换 ε 闭包  J＝ Move(I,a)
    例子：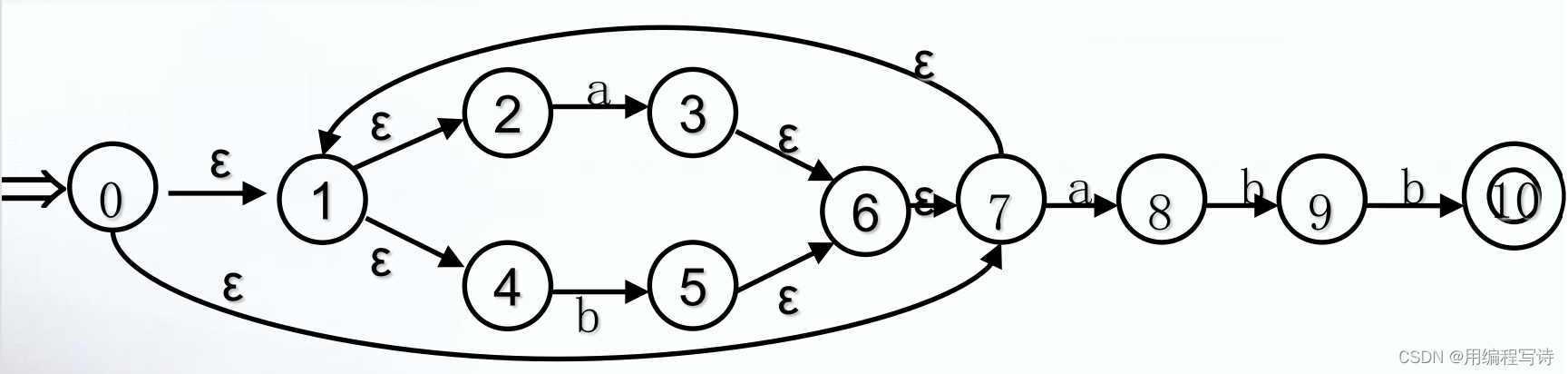
    取 I 0 =ε-closure({0})={0,1,2,4,7}
    标记 I 0 :ε-closure(Move(I 0 ,a))=ε-closure({3,8})={1,2,3,4,6,7,8}=I 1
               ε-closure(Move(I 0 ,b))=ε-closure({5})={1,2,4,5,6,7}=I 2
    标记 I 1 :ε-closure(Move(I 1 ,a))={1,2,3,4,6,7,8}=I 1
               ε-closure(Move(I 1 ,b))={1,2,4,5,6,7,9}=I 3
    标记 I 2 :ε-closure(Move(I 2 ,a))={1,2,3,4,6,7,8}=I 1
               ε-closure(Move(I 2 ,b))={1,2,4,5,6,7}=I 2
    标记 I 3 :ε-closure(Move(I 3 ,a))={1,2,3,4,6,7,8}=I 1
               ε-closure(Move(I 3 ,b))={1,2,4,5,6,7,10}=I 4
    标记 I 4 :ε-closure(Move(I 4 ,a))={1,2,3,4,6,7,8}=I 1
                ε-closure(Move(I 4 ,b))={1,2,4,5,6,7}=I 2
    最后得到的状态矩阵矩阵：

     

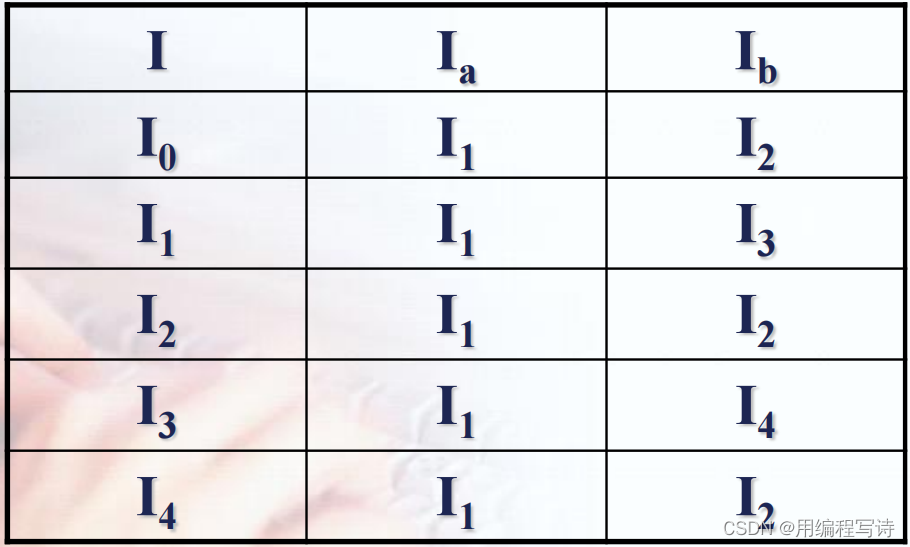    确定化后的DFA图 ：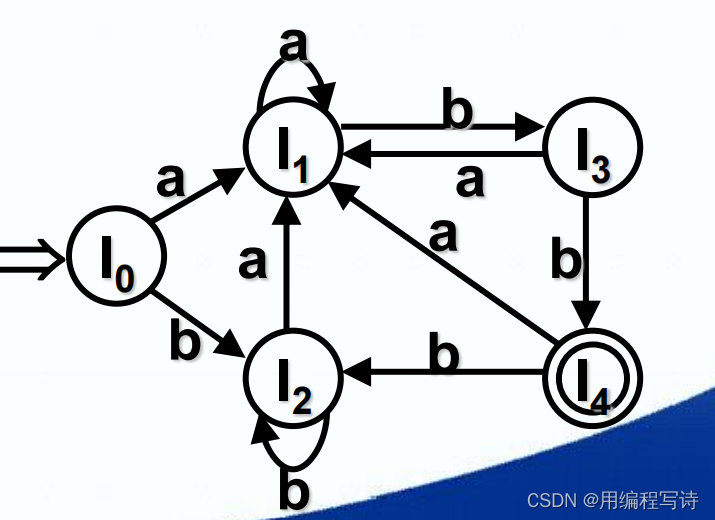
  • 相关阅读:
    RN ScrollView简单实现无限轮播
    微原基础题02
    Unity DOTS Component概述
    Nerfies：可变形神经辐射场
    SMSBMS超市订单管理系统详解（一：准备工作）
    ps2021神经滤镜不能下载,ps2021没法用神经元滤镜
    【Kafka】10道不得不会的 Kafka 面试题
    C++DAY42
    【安卓真机调试】较全面的Android真机调试详解
    Java零基础入门-逻辑运算符
  • 原文地址：https://blog.csdn.net/m0_53345417/article/details/126806676