使用并查集实现查找无向图的连通分量和求解有向图的强连通分量

目录

1.无向图的连通分量

2.求解连通分量算法的实现

3.有向图的强连通分量

4.求解有向图的强连通分量

---

使用C语言实现并查集

有向图和无向图

1.无向图的连通分量

无向图G中，如果存在从顶点v1到顶点v2有路径，那么v1和v2是连通的。

如果对于无向图中的任意两个顶点vi和vj之间都是连通的，那么无向图G是连通图。

连通分量：是无向图中的极大连通子图。

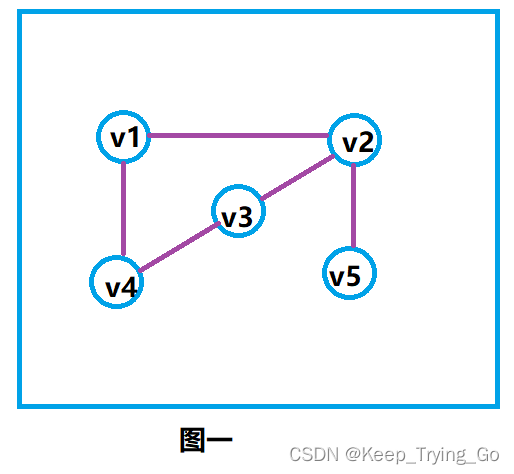
如图一所示为连通图：

如图二所示不是连通图（有是两个连通分量）：

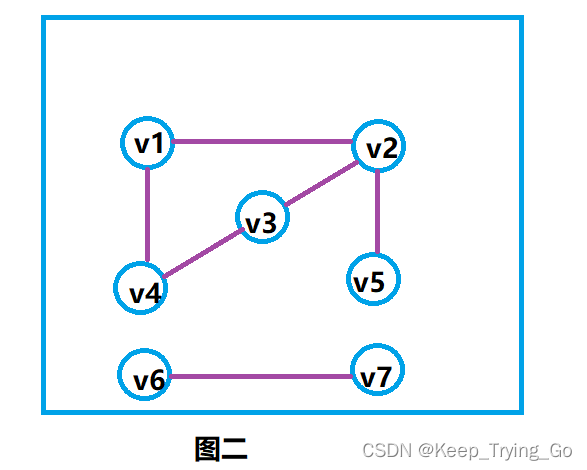
注：由于图二中存在v6,v7和v1,v2,v3,v4,v5是不完全连通的，所以属于两个不同的连通分量，这对于无向图来说是这样，而对于有向图来说的话，判断更加的复杂。

2.求解连通分量算法的实现

思路：首先读者需要对并查集 进行了解，其中主要是查找和合并操作以及路径压缩的方法。由于开始的时候对parent数组初始化都为节点自身，使用rank数组记录每一个集合中合并成的树的高度，将高度矮的合并到高度高的树上；判断无向图的连通分量，就是通过并查集的查找操作，查找到一个节点的根节点，判断这两个节点的根节点是否相同，不同的话表示属于两个集合，也就是两个不同的连通分量。最后就是输出每一个连通分量的集合。

#include<stdio.h>
#include<stdlib.h>
 
#define MAXSIZE 15
 
typedef int ElemType;
 
int parent[MAXSIZE];
int rank[MAXSIZE];
 
void init(){
	for(int i=0;i<MAXSIZE;i++){
		parent[i]=i;
		rank[i]=0;
	}
}
 
//并查集查找操作(包含路径压缩)
int find(int x){
	if(parent[x]==x){
		return x;
	}
	return parent[x]=find(parent[x]);
} 
 
//合并操作
void Union(int x,int y){
	int fx=find(x);
	int fy=find(y);
	//当x和y属于不同的集合时，进行合并操作 
	if(fx!=fy){
		if(rank[fx]>rank[fy]){
			parent[fy]=fx;
		}else{
			parent[fx]=fy;
			if(rank[fx]==rank[fy]){
				rank[fx]++;
			}
		}
	}
} 
 
 
int main(){
	int n,m;
	init();
	printf("请输入无向图的顶点数: ");
	scanf("%d",&n);
	printf("请输入无向图的边数: ");
	scanf("%d",&m);
	printf("请输入无向图的边: \n");
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		Union(u,v);
	} 
	int count=0;
	//note用来记录每个连通分量的根节点 
	int note[MAXSIZE];
	for(int i=1;i<=n;i++){
		int fx=find(i);
		if(fx==i){
			count++;
			note[count]=fx;
		}
	}
	printf("无向连通图的连通分量: %d\n",count);
	for(int i=1;i<=count;i++){
		printf("连通分量[%d]: ",i);
		for(int j=1;j<=n;j++){
			int fx=find(j);
			if(fx==note[i]){
				printf("%d\t",j);
			}
		}
		printf("\n");
	}
	return 0;
}
/*
7 6
 
1 2
1 4
2 3
3 4
2 5
6 7
*/

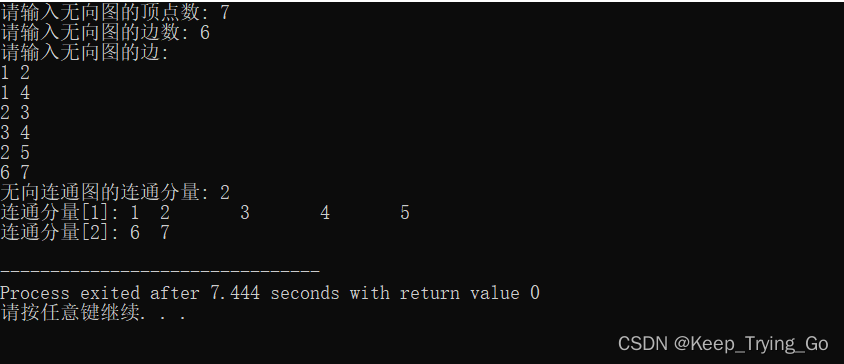
3.有向图的强连通分量

有向图G中，如果对于每一对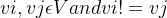,从vi到vj和vj到vi都存在路径，则图G为强连通图。

强连通分量：有向图中的极大连通子图。

如下图所示，虽然原图不是一个强连通图，但是有两个强连通分量：

4.求解有向图的强连通分量

关于深度优先搜索和广度优先搜索请看上面给出的链接。 

思路：首先是进行深度优先遍历，并将遍历的结果存储在finish数组中；正向遍历完成之后就是进行逆向深度优先遍历，正向边使用edge二维数组存储，逆向边使用redge二维数组存储；逆向深度优先遍历的时候使用正向遍历的结果finish，从finish[n]到finish[1]进行遍历，并且使用k来记录强连通分量的个数，Set数组记录强连通分量的集合。

#include<stdio.h>
#include<stdlib.h>
 
#define MAXSIZE 15
 
typedef int ElemType;
 
//用于记录深度优先搜索过程中访问的节点
int finish[MAXSIZE];
//用于记录节点是否被访问
int visit[MAXSIZE];
//记录正向边 
int edge[MAXSIZE][MAXSIZE]; 
//记录反向边
int redge[MAXSIZE][MAXSIZE]; 
//图的顶点数和边数
int n,m; 
//记录强连通分量的集合
int Set[MAXSIZE]; 
//k用来记录强连通分量的个数
int k=0; 
//记录访问的顶点数
int cnt=0; 
 
//初始化
void init(){
	for(int i=0;i<MAXSIZE;i++){
		visit[i]=0;
		finish[i]=0;
		Set[i]=0;
		for(int j=0;j<MAXSIZE;j++){
			edge[i][j]=0;
			redge[i][j]=0;
		}
	}
} 
 
//深度优先搜索
void dfs(int v){
	visit[v]=1;
	for(int i=1;i<=n;i++){
		if(visit[i]==0&&edge[v][i]==1){
			dfs(i);
		}
	}
	//记录访问的节点
	finish[++cnt]=v; 
} 
//反向深度优先搜索
void rdfs(int v,int k){
	visit[v]=1;
	Set[v]=k;
	for(int i=1;i<=n;i++){
		if(visit[i]==0&&redge[v][i]==1){
			rdfs(i,k);
		}
	}
} 
 
//求解强连通分量 
void Solve(){
	//首先进行正向的深度优先搜索
	for(int i=1;i<=n;i++){
		if(visit[i]==0){
			dfs(i);
		}
	} 
	//对visit重新进行初始化
	for(int i=0;i<MAXSIZE;i++){
		visit[i]=0;
	}
	//进行逆向的深度优先搜索
	for(int i=n;i>=1;i--){
		int v=finish[i];
		if(visit[v]==0){
			k++;
			rdfs(v,k);
		}
	}  
}
//输出强连通分量集合
void display(){
	//打印深度优先访问的结果 
	printf("cnt = %d\n",cnt);
	for(int i=1;i<=cnt;i++){
		printf("%d\t",finish[i]);
	}
	printf("\n");
	
	printf("强连通分量的个数: %d\n",k);
	for(int i=1;i<=k;i++){
		printf("强连通分量[%d]: ",i);
		for(int j=1;j<=n;j++){
			if(Set[j]==i){
				printf("%d\t",j);
			}
		}
		printf("\n");
	}
} 
 
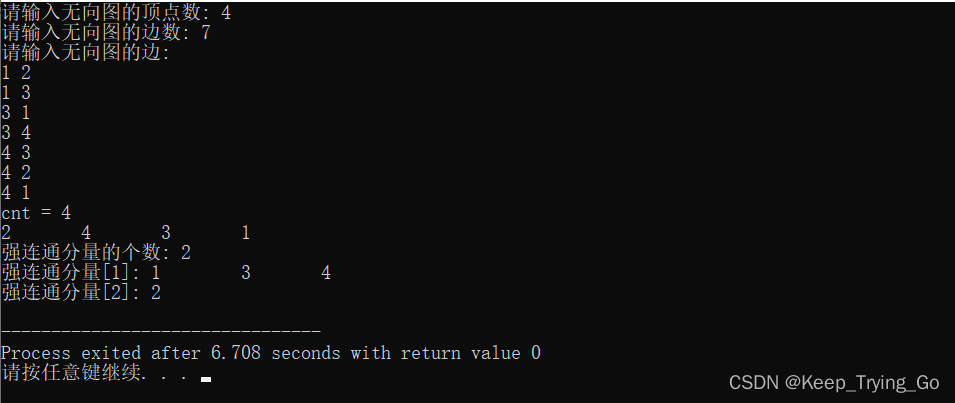
int main(){
	init();
	printf("请输入无向图的顶点数: ");
	scanf("%d",&n);
	printf("请输入无向图的边数: ");
	scanf("%d",&m);
	printf("请输入无向图的边: \n");
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		edge[u][v]=1;
		redge[v][u]=1;
	} 
	Solve();
	display();
	return 0;
}
/*
4 4
 
1 3 
1 2
3 4
4 1
 
4 7
 
1 2
1 3
3 1
3 4
4 3
4 2
4 1
 
7 9
 
1 2
1 3
1 4
2 1 
2 4
5 2
4 5
6 7
7 6
*/