TD Target Algorithms

TD Target Algorithms

1.Sarsa

1.1 名称由来

---

我们容易求出折扣回报$U_t=R_t+\gamma \cdot U_{t+1}$

---

可以进行等式变形。

---

因为无法直接求出期望，考虑用Monte Carlo近似。

---

1.2表格形式

假设states和actions的个数已知，那么可以建立二维table，不断更新table。

---

通过observe 一个状态转移，通过策略函数计算$a_{t+1}$，然后查表$Q_{\pi }$计算TD target。

---

然后计算TD error，更新表中的$Q_{\pi }$

---

1.3 神经网络形式

---

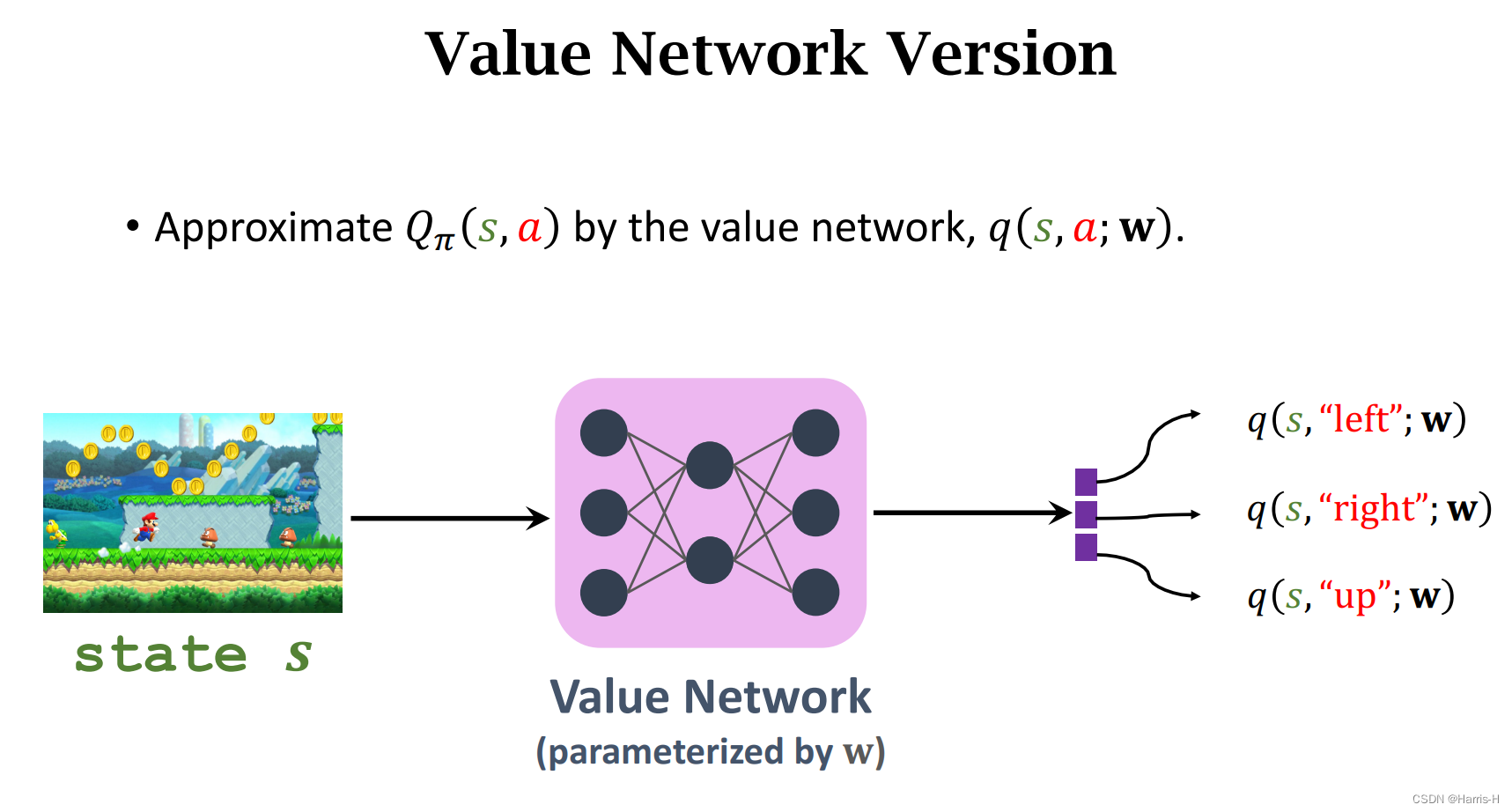
计算TD target 和 TD error，梯度下降更新训练参数$w$。

---

1.4 Summary

---

2.Q-learning

2.1 与Sarsa的区别

---

等式变形可以得到上式。

---

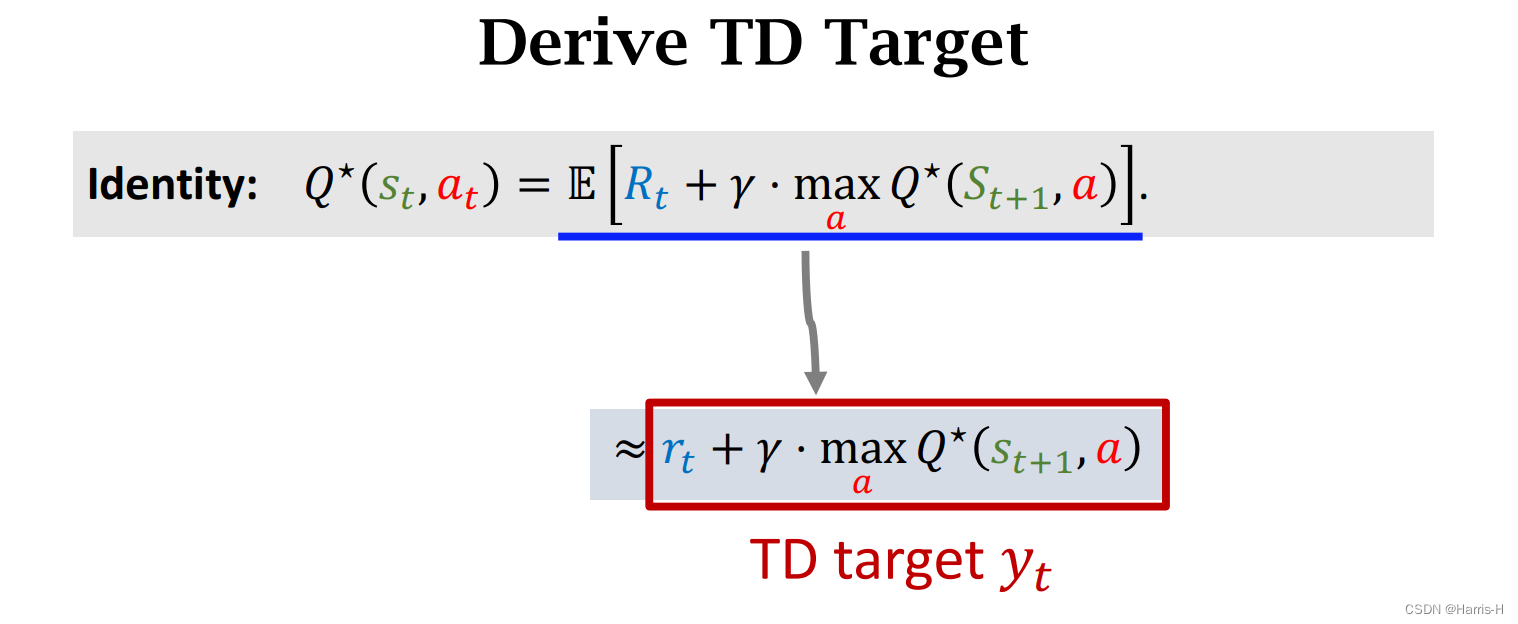
采用Monte Carlo 近似$Q^{\ast }$

2.2 Table形式

---

2.3 DQN形式

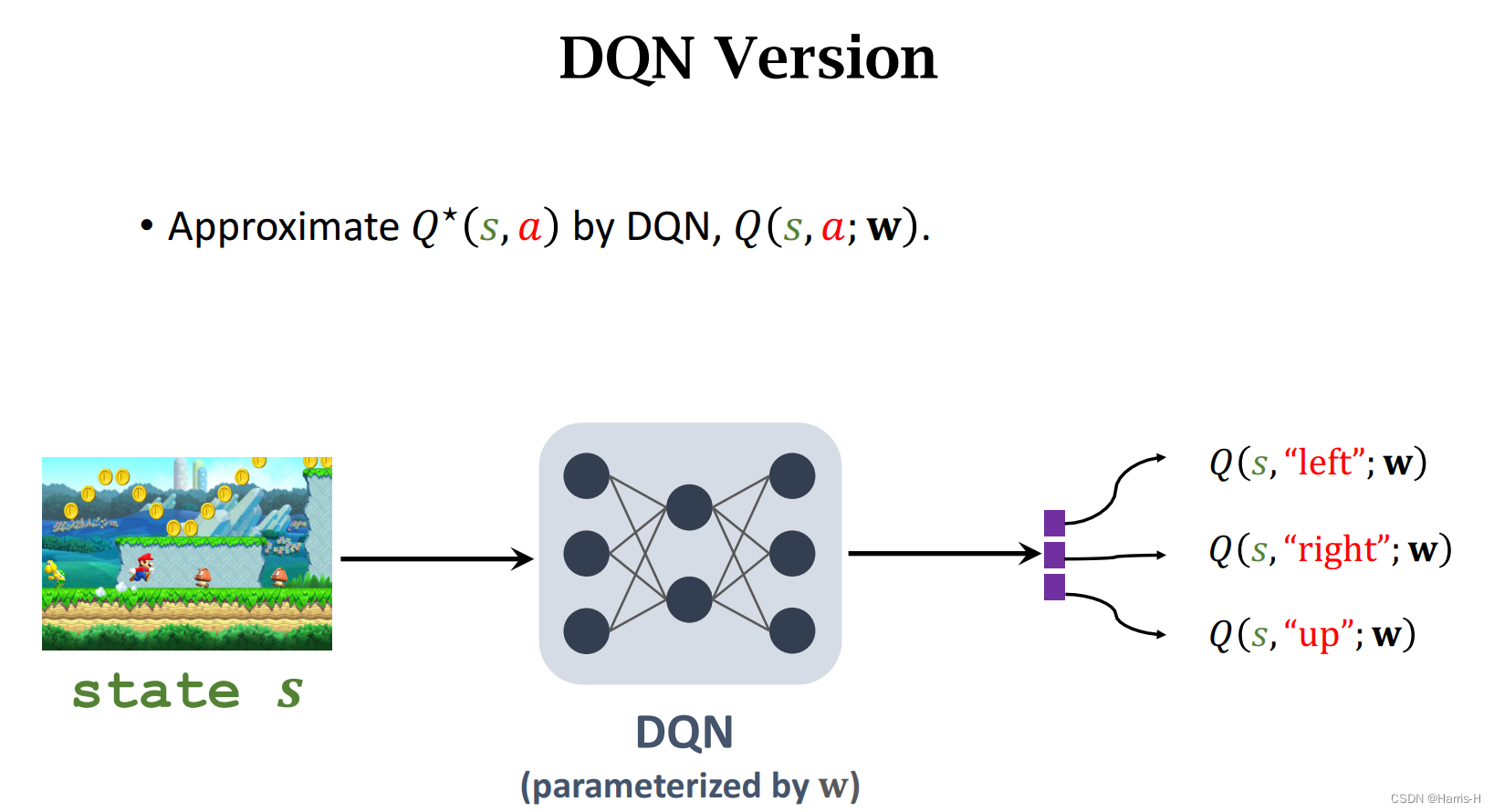
2.4 Summary

---

3.Multi Step TD Target

---

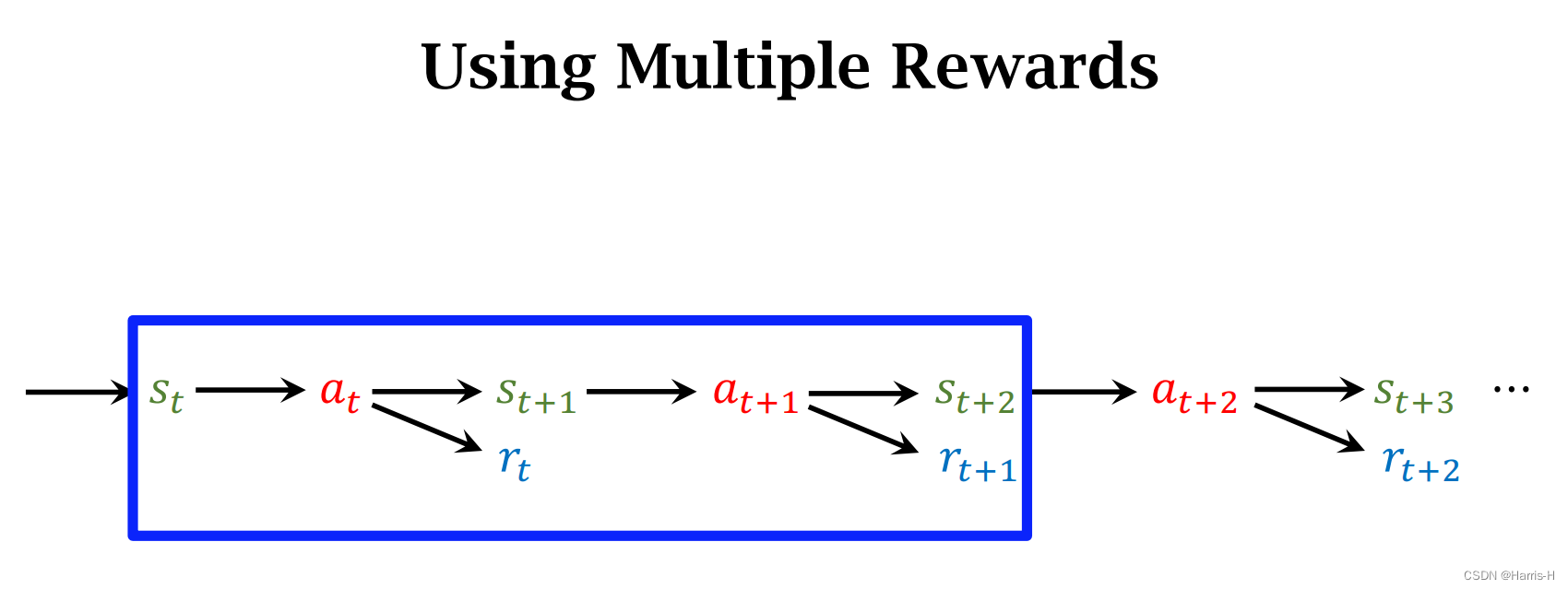
容易得到$U_t$的变形式。

---

Sarsa本质是Multi Step TD 的特殊形式$(m=1)$。

---

Q-learning 同理。

---

因为Multi Step TD Target 更接近真实值，因为$r_t$更真实。所以效果会比One-Step 要好，但是需要考虑性能问题(?)