笔试选择题-图

做过笔试的同学应该知道，数据结构比较常考的除了栈，还有一个数据结构就是图。所以本篇文章就是用来理清图的一些简单的知识点。

图

无点不成图，说明图可以没有边，但不可无点。

• 有向图和无向图：边是否有方向
• 点的度：对无向图，指的是该点所连接的边数；对于有向图，分入度和出度，指向该顶点的边数就是入度，反之就是出度，此时点的度为出度+入度
• 权值：点和边可以有具体的属性含义，称为权值。

存储形式

以无向图为例

1. 邻接矩阵（二维数组）
   
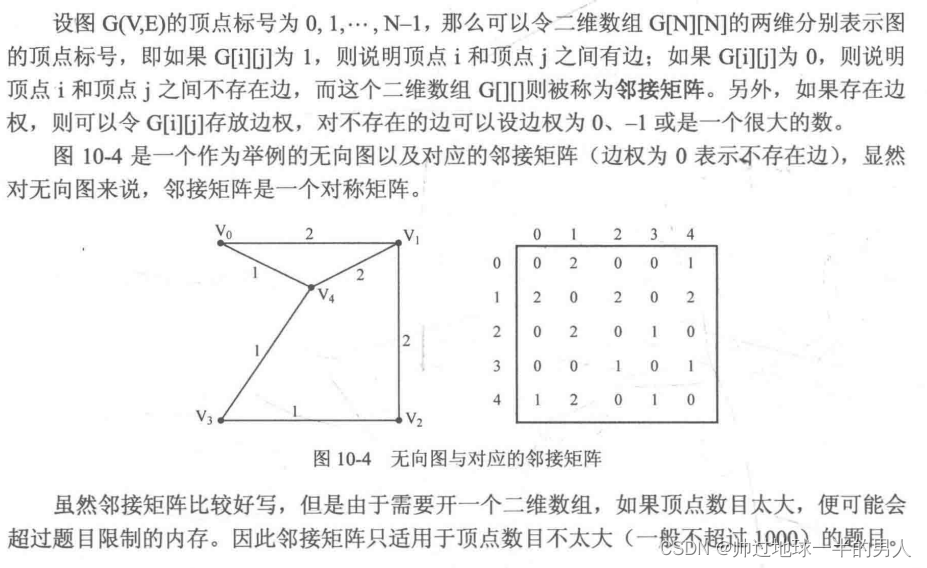
   无向图邻接矩阵是对称的，且顶点的度=某行或者某列非0元素的个数。

2. 邻接表
   只存放有连接的边。节省内存，适合顶点数目较多的场景。List Adj[] 数组可实现。每一个List集合存放每个顶点到其它顶点的信息，Node包含顶点的编号和边的权值
   
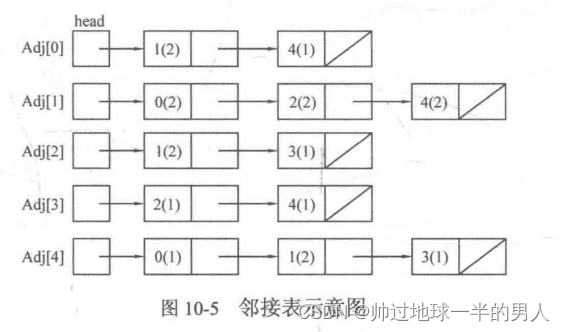
   针对无向图：连通分量
   针对有向图：强连通分量
   
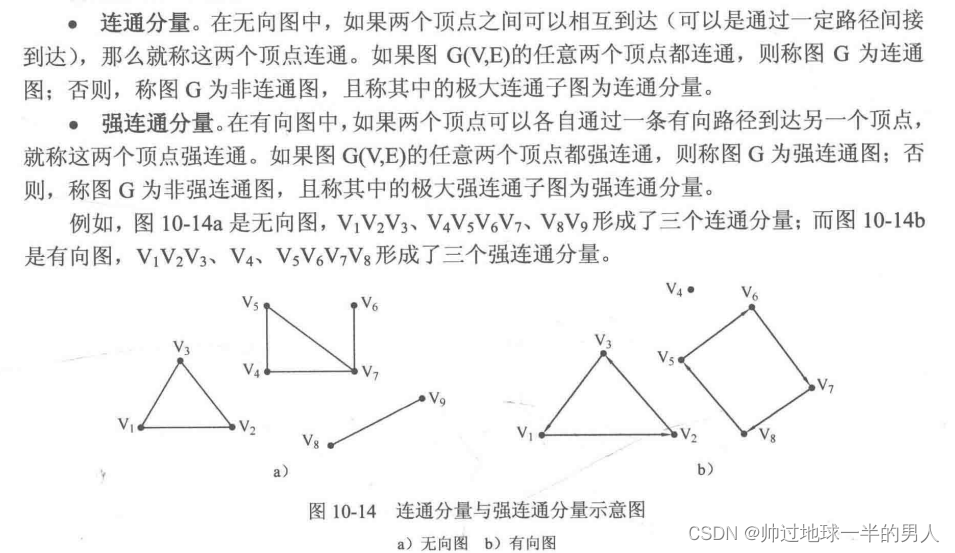
   所谓的（强）连通分量是指，你这个子图，一旦加入其它不在该子图的点，则该子图就不连通。

性质

无向所有顶点的度之和为偶数，因为度=边数*2

有向图所有点的入度之和=出度之和

n个节点的完全有向图含有边的数目为n*(n-1)，每两点之间有两条边相互指向对方，n-1代表每个点有多少条边指向该点(也可以反过来，指向其它点的边）然后有n个点，所以的证。

完全无向图：由于任意两点都有边，从而可得边数为n*(n-1)/2，推导如下，也可以理解为完全有向图的一半

n-1 + n-2 + n-3 +...+2+1
1

n个点的无向连通图的最少边数：n-1。但是如果要求图在任何情况下都是连通的，需要的最少边为:(n-1)*(n-2)/2 + 1，其实就是n-1个点的完全无向图的边数+1，这样就能保证绝对连通。

n个点的有向连通图的最少边数：n，首尾相连

例题

1. 用邻接矩阵法存储一个图时，在不考虑压缩存储的情况下，所占用的存储空间大小只与图中结点个数有关，而与图的边数无关
2. n顶点26边无向图，每个顶点度至少为4，求n的最大值？（三七互娱）
   总度数：262 = 52，顶点度至少为4，说明总度数至少为4n，4*n <= 52，固n最大为13
3. 假设一个无向图中包含 12 个顶点，其中 5 个顶点有 5 个度，7 个顶点有 7 个度，那么这个图有几条边 ？
   度数和边的关系是两倍，从而得37

AOV网和AOE网

• 顶点表示活动，边表示活动间优先关系的有向图称为顶点活动网，即AOV，例如拓扑排序
• 边表示活动，顶点表示事件的有向图称为边活动网，即AOE，例如最短路径
• 关键路径是指AOE 网中的从源点到汇点的最长路径，关键路径上的活动称为关键活动，关键活动会影响整个工程的进度。

拓扑排序

• 若采用邻接矩阵存储一个有向图，且邻接矩阵主对角线以下元素均为0，则该有向图的拓扑序列存在但不唯一。
• 在有向图 G 的拓扑序列中，若顶点 Vi 在顶点 Vj 之前，不可能出现G 中有一条从 Vj 到 Vi 的路径
• 用DFS遍历一个无环有向图，并在DFS算法退栈返回时打印相应的顶点，则输出的顶点序列是逆拓扑有序

最小生成树

设无向图 G 中有 n 个顶点，则该无向图的最小生成树上有n-1条边。
例题
例题
例题

更多

无向图特有:连接多重表。有向图特有:十字链表，边集数组。二者共有:邻接表，邻接矩阵。
例题
哈密顿图