【基于C的排序算法】交换排序之快速排序

前言

本文基于C语言来分享一波笔者对于排序算法的交换排序中的快速排序的学习心得与经验，由于水平有限，纰漏难免，欢迎指正交流。

快速排序

​ 快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
    if(right - left <= 1)
    	return;
    // 按照基准值对array数组的 [left, right)区间中的元素进行划分
    int div = partion(array, left, right);
    // 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
    // 递归排[left, div)
    QuickSort(array, left, div);
    // 递归排[div+1, right)
    QuickSort(array, div+1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

​ 上述为快速排序递归实现的主框架，发现与二叉树前序遍历规则非常像，在写递归框架时想想二叉树前序遍历规则即可快速写出来，只需分析如何按照基准值来对区间中数据进行划分的方式即可。

​ 将区间按照基准值划分为左右两半部分的常见方式有三种。

（以下都是基于要排升序来构思的）

1.hoare版本

基础讲解

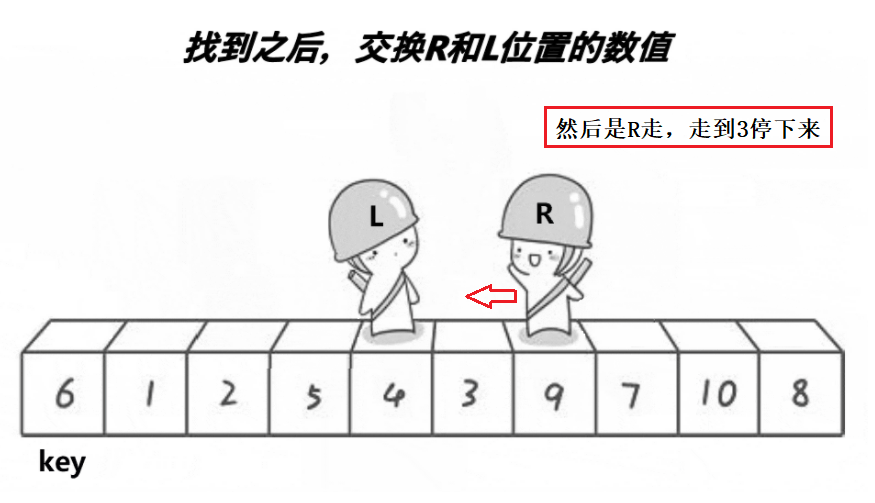
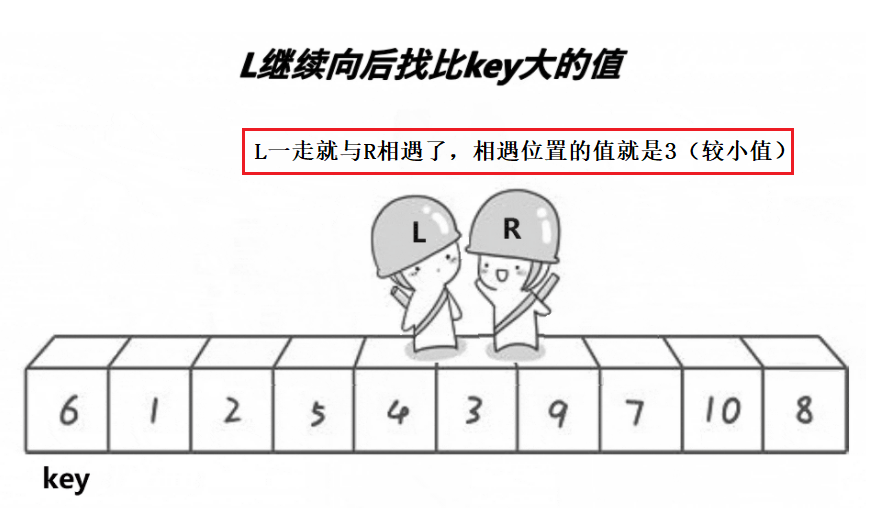
​ 选定一个key值，然后让L和R分别从数组头部和尾部出发，向中间移动，L找比key大的值，R找比key小的值。

如何保证相遇位置的值比key的值要小？

​ 先说一下L和R怎样才会停下来：要么遇到较大值/较小值，要么就是L和R相遇。

​ 只需要把左边第一个元素作为key，并且让右边的R先走（L和R可不是同时开始走的，必然要有一个先走）。

​ 有两种情况：

1. R遇到较小值停下来了，接着是L走，L一直找不到较大值而与R相遇，此时相遇位置的值要比key小。
2. L遇到较大值停下来了，R和L位置的值交换，下一轮开始时注意是R先走，此时L还停着（停着的位置的值在先前的交换中已经变成了较小值了），R一直找不到较小值而与L相遇，此时相遇位置的值要比key小。

​ 同理，如果要把右边第一个元素作为key，则需要让左边的L先走才能保证相遇位置的值比key的值要大。

代码实现

​ 由于我们是要交换数组元素的，key是临时变量的话就不能让key和数组元素交换值，所以可以用下标keyi来搞。

​ 不仅外层while条件是left < right，里面两个while也要加上这个条件，为什么？为了防止找着找着L和R就错过了，也作为L和R相遇的判断条件。同时也要注意是>=和<=，要把相等的情况筛选掉，因为我们要找的是较大值和较小值，如果遇到相等值也停下来的话就会产生干扰。

void Swap(int* px, int* py)
{
    int tmp = *px;
    *px = *py;
    *py = tmp;
}

int PartSort_1(int* arr, int left, int right)
{
 	assert(arr);
    
    int keyi = left;
    while(left < right)
    {
        while(left < right && arr[right] >= arr[keyi])
            --right;
        while(left < right && arr[left] <= arr[keyi])
            ++left;
        if(left < right)//不是因为相遇而停下来才交换，若是相遇就要出循环
            Swap(&arr[left], &arr[right]);
    }
    
    int meeti =  left;
    Swap(&arr[meeti], &arr[keyi]);
    
    return meeti;//返回相遇位置的下标是为了后续分割子区间
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

意义

​ 这只是单趟的排序，它的意义何在呢？

1. key对应的值已经排好了(排好了一个值)。
2. 同时分割出以key为基准的左右两个子区间。如果子区间有序了，整体就有序了。这就涉及到了子问题的递归。

递归实现

​ 实际上在分割出左右子区间后就要用到递归来解决问题了，而这么一个递归的过程用二叉树来描述大概就是这个样子：

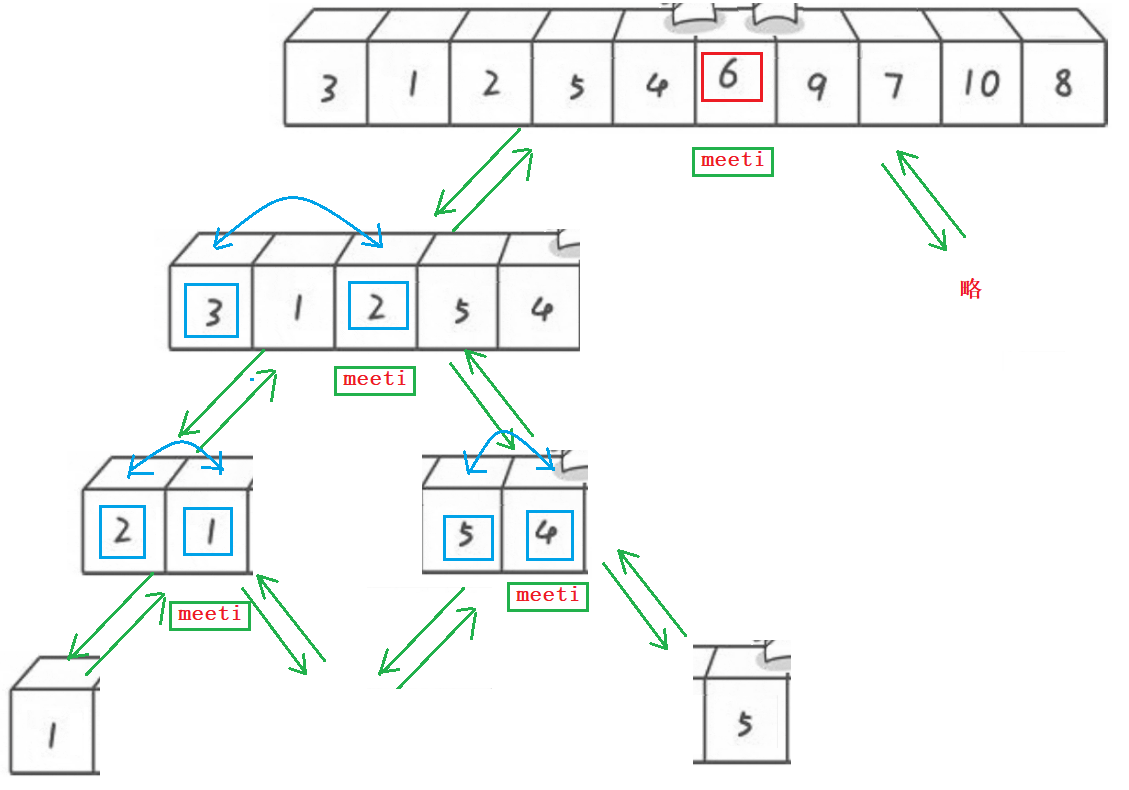
​ meeti就是每次L和R相遇的的位置下标，左右子区间就为[left, meeti - 1]和[meeti + 1, right]，要注意别漏掉了递归终止的条件:if(left >= right)return;如果左边界大于或等于右边界显然说明区间是空区间或者仅有一个元素，不应该再继续递归下去了，此时就要返回上一个函数。

代码实现

void QuickSort(int* arr, int left, int right)
{
    assert(arr);
    
    if(left >= right)
        return;
    
    int meeti = PartSort_1(arr, left, right);
    
    QuickSort(arr, left, meeti - 1);
    QuickSort(arr, meeti + 1, right);
}
1
2
3
4
5
6
7
8
9
10
11
12

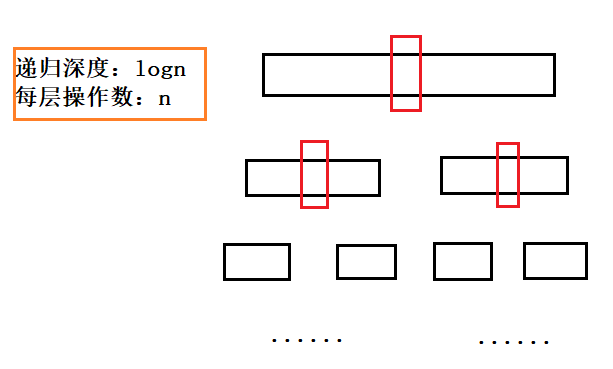
时间复杂度：O(nlogn)

空间复杂度：O(logn)

稳定性：不稳定

​ 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序 。

不足之处

​ 遇到有序或接近有序就完蛋。

​ 因为我们目前选key都是选最左边或最右边的值，接近最小或最大，这样一来，在区间划分和递归时就会出现“一边倒”情况（因为key左边找不到比key大的，右边找不到比key小的），导致递归层数过深容易栈溢出，时间复杂度就变为了O(n²)，效率一下子就低了。

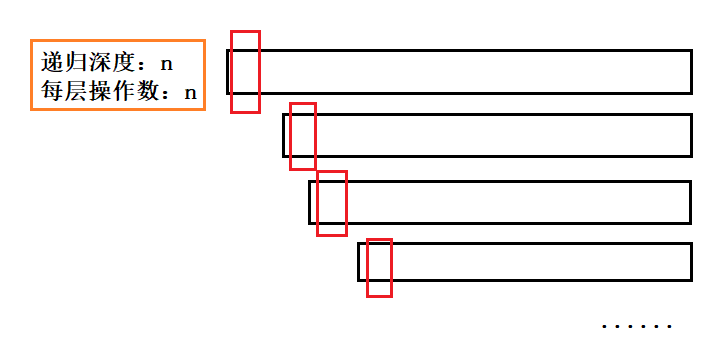
选key思路的优化（三数取中）

​ 那我们可不可以针对这种有序或接近有序的情况来优化一下选key的逻辑呢？

​ 三数取中，也就是从第一个位置、中间位置和最后一个位置的值中选出中间大小的值，把这个中间值换到最前面再继续排序。这样的话怎样都不会选到数组的最大值或最小值，有效规避了有序或接近有序可能带来的不良结果。

​ 写个函数来比较三个数，返回的就是中间值的下标，再把中间值和第一个值交换。

int GetMidIndex(int* arr, int left, int right)
{
    int mid = (right - left) / 2 + left;
    if(arr[left] > arr[mid])
    {
        if(arr[mid] > arr[right])
            return mid;
        else if(arr[right] < arr[left])
            return right;
        else
            return left;
    }
    else
    {
        if(arr[left] > arr[right])
        	return left;
        else if(arr[mid] > arr[right])
            return right;
        else
            return mid;
    }
    
}

int PartSort_1(int* arr, int left, int right)
{
 	assert(arr);
    int mid = GetMidIndex(arr, left, right);
    Swap(&arr[left], &arr[mid]);
    int keyi = left;
    while(left < right)
    {
        while(left < right && arr[right] >= arr[keyi])
            --right;
        while(left < right && arr[left] <= arr[keyi])
            ++left;
        if(left < right)//不是因为相遇而停下来才交换，若是相遇就要出循环
            Swap(&arr[left], &arr[right]);
    }
    
    int meeti =  left;
    Swap(&arr[meeti], &arr[keyi]);
    
    return meeti;//返回相遇位置的下标是为了后续分割子区间
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

小区间优化

​ 当递归到小的子区间时，递归二叉树的结点比较多，可以考虑对小区间使用直接插入排序减少递归量。

​ 由二叉树的性质可知，倒数一二三层加起来的结点数几乎占了总结点数的87.5%，每个结点就是一次递归，当数据量很大的时候，这三层的递归量是很大的，而这三层的区间基本上都是小区间，就几个数比起递归还不如直接排序成本更低。我们这里取8为小区间元素个数基准，只要是小区间就放弃递归而采用直接插入排序。

void InsertSort(int* arr, int sz)
{
    assert(arr);
    
    for(int i = 0; i < sz - 1; ++i)
    {
        int end = i;
        int tmp = arr[end + 1];
        while(end >= 0)
        {
            if(arr[end] > tmp)
            {
                arr[end + 1] = arr[end];
                --end;
            }
            else
                break;

        }
        arr[end + 1] = tmp;        
    }
}

void QuickSort(int* arr, int left, int right)
{
    assert(arr);
    
    if(left >= right)
        return;
    
    if(right - left + 1 <= 8)
    {
        InsertSort(arr + left, right - left + 1);
    }
    else
    {
        int meeti = PartSort_1(arr, left, right);
        QuickSort(arr, left, meeti - 1);
        QuickSort(arr, meeti + 1, right);
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

提醒

​ 有一说一，这个版本要注意的细节比较多，不熟练者容易写bug，所以不太推荐使用。

2.挖坑法

​ 这是hoare的改编版，大体的逻辑框架没有什么区别，主要是一些细节实现的区别，可能让人更好理解接受。

​ 在单趟排序的思路上，虽然仍是最左边的值作为key，L找较大值，R找较小值，但是并不是要交换L和R找到的两个值，而是“填坑”。一开始就把最左边的值暂存到key，此时就形成一个“坑位”，然后让R先走，找较小值，找到的话就把这个值“填坑”，这时候也把较小值所在位置“挖了一个坑”对吧，这就是新的“坑”，挖了就要填，要填得先挖，然后L走也是同理。直到L和R相遇，此时相遇位置也是“坑位”，再把key的值“填坑”即完成本趟排序。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JB5ZhfaD-1662793819275)(https://typora-picture-1313051246.cos.ap-beijing.myqcloud.com/挖坑法.gif)]

int PartSort_2(int* arr, int left, int right)
{
    assert(arr);
    int mid = GetMidIndex(arr, left, right);
    Swap(&arr[left], &arr[mid]);
    int key = arr[left];
    int hole = left;

    while (left < right)
    {
        while (left < right && arr[right] >= key)
            --right;
        if (left < right)
        {
            arr[hole] = arr[right];
            hole = right;
        }
        while (left < right && arr[left] <= key)
            ++left;
        if (left < right)
        {
            arr[hole] = arr[left];
            hole = left;
        }

    }

    arr[hole] = key;
    return hole;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

​ 其他内容没有改变，只是单趟排序的思路有些许变动。

void QuickSort(int* arr, int left, int right)
{
    assert(arr);
    
    if(left >= right)
        return;
    
    if(right - left <= 8)
    {
        InsertSort(arr + left, right - left + 1);
    }
    else
    {
        int meeti = PartSort_2(arr, left, right);
        QuickSort(arr, left, meeti - 1);
        QuickSort(arr, meeti + 1, right);
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

3.前后指针法

​ 这也是hoare的改编版，大体的逻辑框架没有什么区别，主要是一些细节实现的区别。

​ 在单趟排序的思路上，设定两个指针prev和cur，从数组左边向右走，cur先走，cur遇到较小值就停下来，prev走一步，此时交换prev和cur位置的值，然后cur继续走，直到cur走出数组界限，最后把keyi位置的值和prev位置的值交换。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Lh2Dcm7W-1662793819275)(https://typora-picture-1313051246.cos.ap-beijing.myqcloud.com/前后指针.gif)]

int PartSort_3(int* arr, int left, int right)
{
    assert(arr);
    int mid = GetMidIndex(arr, left, right);
    Swap(&arr[left], &arr[mid]);
    int keyi = left;
    int prev = left;
    int cur = left + 1;

    while (cur <= right)
    {
        if (arr[cur] < arr[keyi])
        {
            ++prev;
            Swap(&arr[prev], &arr[cur]);
        }

        ++cur;
    }

    Swap(&arr[prev], &arr[keyi]);
    return prev;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

​ 还可以有一点小小优化：当prev和cur在同一位置时交换就没有意义了，可以多判断一下，省去这些交换。

int PartSort_3(int* arr, int left, int right)
{
    assert(arr);
    int mid = GetMidIndex(arr, left, right);
    Swap(&arr[left], &arr[mid]);
    int keyi = left;
    int prev = left;
    int cur = left + 1;
    
    while(cur <= right)
    {
        if(arr[cur] < arr[keyi] && ++prev != cur)
        	Swap(&arr[prev], &arr[cur]);   
        
        ++cur;
    }
    
    Swap(&arr[keyi], &arr[prev]);
    return prev;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

​ 其他内容没有改变，只是单趟排序的思路有些许变动。

void QuickSort(int* arr, int left, int right)
{
    assert(arr);
    
	if(left >= right)
    	return;

	if(right - left <= 8)
	{
    	InsertSort(arr + left, right - left + 1);
	}
    else
    {
        int meeti = PartSort_3(arr, left, right);
        QuickSort(arr, left, meeti - 1);
        QuickSort(arr, meeti + 1, right);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

非递归实现

​ 使用递归实现在数据量大的时候可能会因为递归太深而栈溢出，要克服这个缺陷可以考虑非递归实现，而想要用非递归来实现，需要对递归实现有着较为深入的理解。

​ 实际上就是要用循环模拟递归，我们这里采用一个栈来存取区间的左右边界，原来的单趟排序PartSort根据传入的左右边界来排序并返回左右子区间的分割点，可以再根据分割点来得到左右子区间的左右边界。

​ 入栈按先左后右顺序，出栈就按先右后左顺序。一开始就把原数组左右边界入栈，进入循环后只要栈不为空就继续。实质上就是利用栈的先进后出，先放右区间再放左区间，取的时候就先取出左区间，左区间PartSort一下后又把它的右区间先入栈、左区间后入栈，等下一次取的时候还是左区间，以此类推，是不是就模拟了递归时先左后右呢？

​ 一定注意不要漏了if(left >= right)continue;，区间为空或仅有一个元素时就不需要再PartSort了。

void QuickSortNonR(int* arr, int begin, int end)
{
    assert(arr);

    ST st;
    StackInit(&st);

    int left = begin;
    StackPush(&st, left);

    int right = end;
    StackPush(&st, right);

    while(!StackEmpty(&st))
    {
        right = StackTop(&st);
        StackPop(&st);
        left = StackTop(&st);
        StackPop(&st);

        if (left >= right)
            continue;

        int keyi = PartSort_1(arr, left, right);
        //先放右区间
        StackPush(&st, keyi + 1);
        StackPush(&st, right);
        //再放左区间
        StackPush(&st, left);
        StackPush(&st, keyi - 1);

    }

    StackDestroy(&st);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

感谢观看，你的支持就是对我最大的鼓励~