OpenGL - PBR

PBR，或者用更通俗一些的称呼是指基于物理的渲染(Physically Based Rendering)，它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。正因为基于物理的渲染目的便是为了使用一种更符合物理学规律的方式来模拟光线，看起来要更真实一些。

到微观尺度之后任何平面都可以用被称为微平面(Microfacets)的细小镜面来进行描绘。根据平面粗糙程度的不同，这些细小镜面的取向排列可以相当不一致，微平面的取向方向与中间向量的方向越是一致，镜面反射的效果就越是强烈越是锐利。然后再加上一个介于0到1之间的粗糙度参数，这样我们就能概略的估算微平面的取向情况了：

反射光与折射光它们二者之间是互斥的关系。无论何种光线，其被材质表面所反射的能量将无法再被材质吸收。因此，诸如折射光这样的余下的进入表面之中的能量正好就是我们计算完反射之后余下的能量。

float kS = calculateSpecularComponent(...); // 反射/镜面 部分
float kD = 1.0 - ks;                        // 折射/漫反射 部分
1
2

基于物理的渲染所坚定的遵循的是一种被称为反射率方程(The Reflectance Equation)的渲染方程的特化版本。

Lo表示了从ωo方向上观察，光线投射到点p上反射出来的辐照度，即所有投射到点p上的光线的总和。
fr被称为BRDF，或者双向反射分布函数(Bidirectional Reflective Distribution Function) ，它的作用是基于表面材质属性来对入射辐射率进行缩放或者加权。


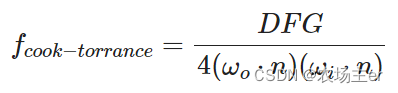
三个函数分别为法线分布函数(Normal Distribution Function)，菲涅尔方程(Fresnel Rquation)和几何函数(Geometry Function)：

• 法线分布函数：估算在受到表面粗糙度的影响下，取向方向与中间向量一致的微平面的数量。这是用来估算微平面的主要函数。
• 几何函数：描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
• 菲涅尔方程：菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。

在下面你可以看到在一个PBR渲染管线当中经常会碰到的纹理列表，还有将它们输入PBR渲染器所能得到的相应的视觉输出：

• 反照率：反照率(Albedo)纹理为每一个金属的纹素(Texel)（纹理像素）指定表面颜色或者基础反射率。这和我们之前使用过的漫反射纹理相当类似，不同的是所有光照信息都是由一个纹理中提取的。漫反射纹理的图像当中常常包含一些细小的阴影或者深色的裂纹，而反照率纹理中是不会有这些东西的。它应该只包含表面的颜色（或者折射吸收系数）。
• 法线：法线贴图纹理和我们之前在法线贴图教程中所使用的贴图是完全一样的。法线贴图使我们可以逐片段的指定独特的法线，来为表面制造出起伏不平的假象。
• 金属度：金属(Metallic)贴图逐个纹素的指定该纹素是不是金属质地的。根据PBR引擎设置的不同，美术师们既可以将金属度编写为灰度值又可以编写为1或0这样的二元值。
• 粗糙度：粗糙度(Roughness)贴图可以以纹素为单位指定某个表面有多粗糙。采样得来的粗糙度数值会影响一个表面的微平面统计学上的取向度。一个比较粗糙的表面会得到更宽阔更模糊的镜面反射（高光），而一个比较光滑的表面则会得到集中而清晰的镜面反射。某些PBR引擎预设采用的是对某些美术师来说更加直观的光滑度(Smoothness)贴图而非粗糙度贴图，不过这些数值在采样之时就马上用（1.0 – 光滑度）转换成了粗糙度。
• AO：环境光遮蔽(Ambient Occlusion)贴图或者说AO贴图为表面和周围潜在的几何图形指定了一个额外的阴影因子。比如如果我们有一个砖块表面，反照率纹理上的砖块裂缝部分应该没有任何阴影信息。然而AO贴图则会把那些光线较难逃逸出来的暗色边缘指定出来。在光照的结尾阶段引入环境遮蔽可以明显的提升你场景的视觉效果。网格/表面的环境遮蔽贴图要么通过手动生成，要么由3D建模软件自动生成。

#version 330 core
out vec4 FragColor;
in vec2 TexCoords;
in vec3 WorldPos;
in vec3 Normal;

// material parameters
uniform vec3  albedo;
uniform float metallic;
uniform float roughness;
uniform float ao;

// lights
uniform vec3 lightPositions[4];
uniform vec3 lightColors[4];

uniform vec3 camPos;

const float PI = 3.14159265359;

float DistributionGGX(vec3 N, vec3 H, float roughness);
float GeometrySchlickGGX(float NdotV, float roughness);
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness);
vec3 fresnelSchlickRoughness(float cosTheta, vec3 F0, float roughness);

void main()
{       
    vec3 N = normalize(Normal);
    vec3 V = normalize(camPos - WorldPos);

    vec3 F0 = vec3(0.04); 
    F0 = mix(F0, albedo, metallic);

    // reflectance equation
    vec3 Lo = vec3(0.0);
    for(int i = 0; i < 4; ++i) 
    {
        // calculate per-light radiance
        vec3 L = normalize(lightPositions[i] - WorldPos);
        vec3 H = normalize(V + L);
        float distance    = length(lightPositions[i] - WorldPos);
        float attenuation = 1.0 / (distance * distance);
        vec3 radiance     = lightColors[i] * attenuation;        

        // cook-torrance brdf
        float NDF = DistributionGGX(N, H, roughness);        
        float G   = GeometrySmith(N, V, L, roughness);      
        vec3 F    = fresnelSchlick(max(dot(H, V), 0.0), F0);       

        vec3 kS = F;
        vec3 kD = vec3(1.0) - kS;
        kD *= 1.0 - metallic;     

        vec3 nominator    = NDF * G * F;
        float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0) + 0.001; 
        vec3 specular     = nominator / denominator;

        // add to outgoing radiance Lo
        float NdotL = max(dot(N, L), 0.0);                
        Lo += (kD * albedo / PI + specular) * radiance * NdotL; 
    }   

    vec3 ambient = vec3(0.03) * albedo * ao;
    vec3 color = ambient + Lo;

    color = color / (color + vec3(1.0));
    color = pow(color, vec3(1.0/2.2));  

    FragColor = vec4(color, 1.0);
}  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70