极线的绘制（已知相机的内外参数，极线几何）

极线几何与立体视觉
目标：
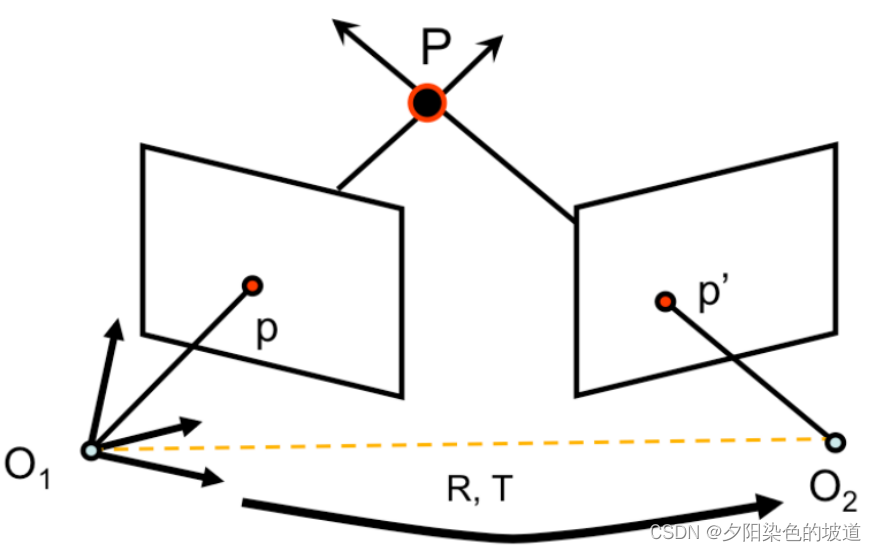
极限几何的约束网上有很多资料，但是大多数是理论知识和一些推导。但是在具体的应用中，**常常拿极限约束来判断相机的位姿是否准确，对于这个介绍相对较少。**本博客将介绍在一直相机的内外参数的情况下，怎么实现两个相机的极限约束。

双目视觉对应关系，同时也可用于相邻两帧间的运动估计。见下图：

配点必须在极线上
基线：左右像机光心连线（黄色线段$O_1{O}_2$）；
极平面：空间点，两像机光心决定的平面（灰色平面$O_{1}P{O}_2$）；
极点：基线与两摄像机图像平面的交点；
极线：极平面与图像平面交线（蓝色线段）

基于极限的几何关系，需要知道它们的参数关系如下。
两个相机的转化为$R,T$.
如果知道两个相机的内外参数。可以计算它们的转化矩阵。假设中左边的相机为世界坐标系。它们可以表示为：

上述是假设两个相机之前的关系。其中世界坐标系为左边相机的坐标系。它们重合。因此通过$R,T$计算得到的第二个相机的参数(它是相机位姿态，它是指的是在第一个坐标系下的$R,T$)，
具体的计算可以参考如下。
$p_2$坐标点（原本在$O_2$坐标系）转化为在$O_{\mathrm{１}}$坐标系$p_{\mathrm{１}}$的（$p_1$表示它在$O_1$坐标系下的坐标）坐标为：
$$p_{\mathrm{１}}=R{p}_{\mathrm{２}}+T=>p_{\mathrm{２}}=R^T{p}_{\mathrm{１}}-R^{T}T(1)$$
上述可以得到，从$O_{\mathrm{１}}$坐标系转换到$O_{\mathrm{２}}$坐标系为：
$[R^T-R^{T}T]$

因此两个相互转换的矩阵为:
$[R,T]$：表示从$O_{\mathrm{２}}$坐标系到$O_{\mathrm{１}}$坐标系的转换。
$[R^T-R^{T}T]$：表示从$O_{\mathrm{１}}$坐标系到$O_{\mathrm{２}}$坐标系的转换。

最后加上相机的内参矩阵$K,K^{\prime }$可以得到整体的矩阵转换如下：

$$M=K[I0],M^{\prime }=K^{\prime }[R^T-R^{T}T]$$

为了方便计算，假设相机的内参矩阵$K,K^{\prime }$为单位矩阵$I$。因此
$$M=[I0],M^{\prime }=[R^T-R^{T}T]$$

从图二可以知道$p^{\prime }$在坐标系$O_1$的坐标为：$R{p}^{\prime }+T$,因为$R{p}^{\prime }+T$这个点在$O_1$坐标系的极线$O_{1}P$上，因为极限平面$O_1{O}_{2}P$是平面：
$$T\times (R{p}^{\prime }+T)=T\times (R{p}^{\prime })(2)$$
向量$T\times (R{p}^{\prime })$表示垂直于平面$O_1{O}_{2}P$
利用叉乘得到：
$$p^T\cdot [T\times (R{p}^{\prime })]=0(3)$$
其中叉乘$Ｔ$可以表示为矩阵形式，一般表示为$skew(T)$或者$[T_{\times }]$
$$[T_{\times }]=\left[\begin{array}{ccc}0& -T[2]& T[1]\\ T[2]& 0& -T[0]\\ -T[1]& T[0]& 0\end{array}\right](4)$$
公式$(3)$写成矩阵的形式为：
$$p^T\cdot [T\times (R{p}^{\prime })]=0=>p^T[T_{\times }]R{p}^{\prime }=0(5)$$
从公式$(5)$得到$[T_{\times }]R$为Essential Matrix,这个矩阵写成：$[T_{\times }]R=E$,因此：
$$p^{T}E{p}^{\prime }=0(6)$$
直线的表达为$l\cdot p=0$(在齐次坐标表示下)
可以把$E{p}^{\prime }$看做是直线的方程，$p$看做是直线上的点，也就是说$E{p}^{\prime }$就是以$O_1$为原点坐标系中的极线了（图一$O_{1}e$线段），反之也可。

上述都是将$K,K^{\prime }$设置为单位矩阵。当不再是单位矩阵的时候。得到矩阵为”
$$M=K[I0],M^{\prime }=K^{\prime }[R^T-R^{T}T](7)$$
因为$K,K^{\prime }$是相机内参数，它表示从相机坐标系转换为图像坐标系上。因此：$p_I=K^{-1}p$; $p_I^{\prime }=K^{\prime -1}{p}^{\prime }$
因为公式：
$$p^{T}E{p}^{\prime }=0(6)$$
将$p_I=K^{-1}p$; $p_I^{\prime }=K^{\prime -1}{p}^{\prime }$ 带入$(6)$得到：

$$p^T{K}^{-T}[T_{\times }]R{K}^{\prime -1}{p}^{\prime }=0(8)$$
将$F=K^{-T}[T_{\times }]R{K}^{\prime -1}$,这就是Fundamental Matrix了。也是opencv里面计算的Fundametal矩阵

上述都是将第一个相机设置为和世界坐标系一致。但是在一直两个相机的情况下。可能需要计算$R,T$矩阵。它们是：表示从$O_{\mathrm{２}}$坐标系到$O_{\mathrm{１}}$坐标系的转换。
已知两个相机(都是相机的外参)为：
$$\begin{gathered} M_{\mathrm{１}}=\left[\begin{array}{cc}{R}_1& T_1\\ 0& 1\end{array}\right] \\ {M}_2=\left[\begin{array}{cc}{R}_2& T_2\\ 0& 1\end{array}\right] \end{gathered}$$
需要计算从$O_{\mathrm{２}}$坐标系到$O_{\mathrm{１}}$坐标系的转换的矩阵$R,T$
推导：
假设两个对应点在各自的相机坐标系为$p_1$,$p_2$
$p_1$在世界坐标系的顶点为
$$p_w=M_1{p}_1(9)$$
$p_2$在世界坐标系的顶点为
$$p_w=M_2{p}_2(10)$$
$(9)(10)$公式得到：
$$p_{\mathrm{１}}=M_1^{-1}{M}_2{p}_2$$
其中$R,T$为$M_1^{-1}{M}_2$旋转矩阵和平移向量。
代码如下：

void RunTwoImagesCorrspondEpilinesWithPath(int src_idx, int tgt_idx, const std::string& dir)
{
	std::cerr << "the cams num: " << cams_modes_.size() << std::endl;
	if (src_idx < 0 || tgt_idx < 0 ||
		src_idx >= cams_modes_.size() || tgt_idx >= cams_modes_.size())
	{
		std::cerr << "RunTwoImagesCorrespondEpilines invalid idx..." << std::endl;
		return;
	}
	if (!cams_modes_[src_idx].valid_ || !cams_modes_[tgt_idx].valid_)
	{
		std::cerr << "RunTwoImagesCorrespondEpilines invalid cams existed..." << std::endl;
		return;
	}
	CameraModel src_cam_model = cams_modes_[src_idx];
	CameraModel tgt_cam_model = cams_modes_[tgt_idx];
	std::string src_name = images_files_path_[src_idx];
	std::string tgt_name = images_files_path_[tgt_idx];
	std::cerr << "src_name: " << src_name << std::endl;
	std::cerr << "tgt_name: " << tgt_name << std::endl;
	std::string src_file_name = src_name.substr(src_name.find_last_of("/") + 1, src_name.find_last_of(".") - src_name.find_last_of("/") - 1);
	std::string tgt_file_name = tgt_name.substr(tgt_name.find_last_of("/") + 1, tgt_name.find_last_of(".") - tgt_name.find_last_of("/") - 1);
	cv::Mat src_rgb = cv::imread(src_name);
	cv::Mat tgt_rgb = cv::imread(tgt_name);
	//cv::imshow("tgt_rgb", tgt_rgb);
	//cv::waitKey(0);
	// used in OpenCV3
	cv::Ptr<cv::FeatureDetector> detector = cv::ORB::create();
	cv::Ptr<cv::DescriptorExtractor> descriptor = cv::ORB::create();
	std::vector< cv::KeyPoint > src_kp, tgt_kp;
	detector->detect(src_rgb, src_kp);
	detector->detect(tgt_rgb, tgt_kp);
	// ¼ÆËãÃèÊö×Ó
	cv::Mat src_desp, tgt_desp;
	descriptor->compute(src_rgb, src_kp, src_desp);
	descriptor->compute(tgt_rgb, tgt_kp, tgt_desp);
	// Æ¥ÅäÃèÊö×Ó
	std::vector< cv::DMatch > matches;
	cv::BFMatcher matcher;
	matcher.match(src_desp, tgt_desp, matches);
	cout << "Find total " << matches.size() << " matches." << endl;
	if (matches.size() < match_pnts_num_)
	{
		std::cerr << "match num is too much fewer..." << std::endl;
		return;
	}
	// ɸѡƥÅä¶Ô
	std:vector< cv::DMatch > goodMatches;
	double minDis = 9999;
	for (size_t i = 0; i < matches.size(); i++)
	{
		if (matches[i].distance < minDis)
			minDis = matches[i].distance;
	}
	for (size_t i = 0; i < matches.size(); i++)
	{
		if (matches[i].distance < 10 * minDis)
			goodMatches.push_back(matches[i]);
	}
	std::vector< cv::Point2f > src_pts, tgt_pts;
	for (size_t i = 0; i<goodMatches.size(); i++)
	{
		src_pts.push_back(src_kp[goodMatches[i].queryIdx].pt);
		tgt_pts.push_back(tgt_kp[goodMatches[i].trainIdx].pt);
	}
	//通过两个相机的位姿计算它们之间的e_matrix
	Eigen::Matrix4f src_pose = src_cam_model.cam_pose_;
	Eigen::Matrix4f tgt_pose = tgt_cam_model.cam_pose_;
	Eigen::Matrix4f src_extr = src_pose.inverse();
	Eigen::Matrix4f tgt_extr = tgt_pose.inverse();
	Eigen::Matrix4f relative_extr = tgt_extr*src_pose;
	Eigen::Matrix3f r_extr = relative_extr.topLeftCorner(3, 3);
	Eigen::Vector3f t_extr = relative_extr.topRightCorner(3, 1);
	//
	Eigen::Matrix3f em = ComputeCrossMatrixFromLVector(t_extr)*r_extr;
	//已知e_matrix，计算fundamental_matrix
	Eigen::Matrix3f src_km = Eigen::Matrix3f::Identity();
	Eigen::Matrix3f tgt_km = Eigen::Matrix3f::Identity();	
	src_km(0, 0) = src_cam_model.fx_;
	src_km(1, 1) = src_cam_model.fy_;
	src_km(0, 2) = src_cam_model.cx_;
	src_km(1, 2) = src_cam_model.cy_;
	tgt_km(0, 0) = src_cam_model.fx_;
	tgt_km(1, 1) = src_cam_model.fy_;
	tgt_km(0, 2) = src_cam_model.cx_;
	tgt_km(1, 2) = src_cam_model.cy_;
	Eigen::Matrix3f fm = (tgt_km.inverse()).transpose()*em*src_km.inverse();
	std::cerr << "fm: \n" << fm << std::endl;
	Eigen::Matrix3f fmt = fm;
	//²âÊÔ
	cv::Mat fundm = (cv::Mat_<float>(3, 3)
		<< fmt(0, 0), fmt(0, 1), fmt(0, 2),
		fmt(1, 0), fmt(1, 1), fmt(1, 2),
		fmt(2, 0), fmt(2, 1), fmt(2, 2));
	std::cerr << fundm << std::endl;
	std::vector<cv::Vec<float, 3>> epilines1, epilines2;
	computeCorrespondEpilines(src_pts, 1, fundm, epilines1);
	computeCorrespondEpilines(tgt_pts, 2, fundm, epilines2);
	cv::RNG &rng = cv::theRNG();
	for (int i = 0; i < match_pnts_num_; ++i) {
		//Ëæ»ú²úÉúÑÕÉ«
		std::cerr << "epilines1: " << i << ": " << epilines1[i] << std::endl;
		std::cerr << "epilines2: " << i << ": " << epilines2[i] << std::endl;
		cv::Scalar color = cv::Scalar(rng(255), rng(255), rng(255));
		circle(src_rgb, src_pts[i], 5, color, 3);
		//»æÖÆÍ⼫ÏßµÄʱºò£¬Ñ¡ÔñÁ½¸öµã£¬Ò»¸öÊÇx=0´¦µÄµã£¬Ò»¸öÊÇxΪͼƬ¿í¶È´¦
		line(src_rgb, cv::Point(0, -epilines2[i][2] / epilines2[i][1]), cv::Point(src_rgb.cols, -(epilines2[i][2] + epilines2[i][0] * src_rgb.cols) / epilines2[i][1]), color);
		circle(tgt_rgb, tgt_pts[i], 5, color, 3);
		line(tgt_rgb, cv::Point(0, -epilines1[i][2] / epilines1[i][1]), cv::Point(tgt_rgb.cols, -(epilines1[i][2] + epilines1[i][0] * tgt_rgb.cols) / epilines1[i][1]), color);
	}
	std::string abs_src_file_name = dir + "/" + src_file_name + ".png";
	std::string abs_tgt_file_name = dir + "/" + tgt_file_name + ".png";
	std::cerr << "abs_src_file_name: " << abs_src_file_name << std::endl;
	std::cerr << "abs_tgt_file_name: " << abs_tgt_file_name << std::endl;
	//std::system("pause");
	//cv::imshow("epiline1", tgt_rgb);
	//cv::waitKey(0);
	//std::cerr << "tgt_rgb rows, cols: " << tgt_rgb.rows << ", " << tgt_rgb.cols << std::endl;
	//std::system("pause");
	cv::imwrite(abs_tgt_file_name, tgt_rgb);
	//std::system("pause");
	//cv::imshow("epiline2", src_rgb);
	cv::imwrite(abs_src_file_name, src_rgb);
	cv::waitKey(0);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125

测试的结果如下：