《代码大全2》第17章 不常见的控制结构

目录

前言

17.1 子程序中的多处返回

17.2 递归

17.2.1 递归的例子

17.2.2 使用递归的技巧

17.3 goto

17.4 针对不常见控制结构的观点

核对表：不常见的控制结构

return

递归

---

《Code_Complete_2》持续更新中......_@来杯咖啡的博客-CSDN博客这本书有意设计成使你既可以从头到尾阅读，也可以按主题阅读。1. 如果你想从头到尾阅读，那么你可以直接从第2章“用隐喻来更充分地理解软件开发”开始钻研。2. 如果你想学习特定的编程技巧，那么你可以从第6章“可以工作的类”开始，然后根据交叉引用的提示去寻找你感兴趣的主题。3. 如果你不确定哪种阅读方式更适合你，那么你可以从第3章3.2节“辦明你所从事的软件的类型”开始。.....................https://blog.csdn.net/qq_43783527/article/details/126275083

前言

        有些控制结构处在这样的尴尬境地中：有时被人当做最前沿的编程要素，有时却又会被批判得声名狼藉——这些情况甚至常常同时发生！这些结构不是所有语言都有的，但如果在提供这些结构的语言中谨慎地使用它们，你将会获得很多帮助。

17.1 子程序中的多处返回

        多数语言都提供了某种半途退出子程序的方法。程序可以通过 return 和 exit这类控制结构，在任何需要的时候退出子程序。它导致子程序按照正常的退出途径终止，并把控制权转交给调用方子程序。在这里，我们用 return 这一词语泛指C++和 Java 中的 return, Microsoft Visual Basic 中的 Exit Sub 和 Exit Function， 以及与之相似的其他结构。

        下面给出一些使用 return 语句的指导原则：
        1、如果能增强可读性，那么就使用 return。 在某些子程序里，一旦知道了答案，你会希望马上返回到调用方子程序。如果子程序被定义为检测出错误以后不再做任何更多的清理操作，那么不马上返回就意味着你还得写更多的代码。

        下面就是一个好例子，它演示了一种需要从子程序里的多个位置返回的合理情况：

         2、用防卫子句（guard clause)（早返回或早退出）来简化复杂的错误处理。 如果代码中必须要在执行正常操作之前做大量的错误条件检测，就很可能导致代码的缩进层次过深，并且遮蔽正常情况的执行路径，如下所示：

从审美的角度来说，把子程序的主体缩在4条 if 语句里面很难看，尤其是当最里层 if语句的代码非常多的时候。在这种情况下，如果先检查错误情况，用这些代码来为正常的执行路径清路，那么代码的布局有时可能变得更清楚。下面给出一个这种方法的示例：

         3、减少每个子程序中 return 的数量。 如果在读子程序的后部时，你没有意识到它从前面某个地方返回的可能性，想理解这个子程序就很困难。由此可见，使用return 要十分审慎——只当它们能增强可读性的时候才去使用。

17.2 递归

        在递归（recursion）里面，一个子程序自己负责解决某个问题的一小部分，它还把问题分解成很多的小块，然后调用自己来分别解决每一小块。当问题的小部分很容易解决，而问题的大部分也很容易分解成众多的小部分时，常常会用到递归。

17.2.1 递归的例子

        假设你有一个表示迷宫的数据类型。从本质上主说一米宝就星一个网格，在网格的每一个点，你都有可能向上下左右四个方向以往不止一个方向移动。

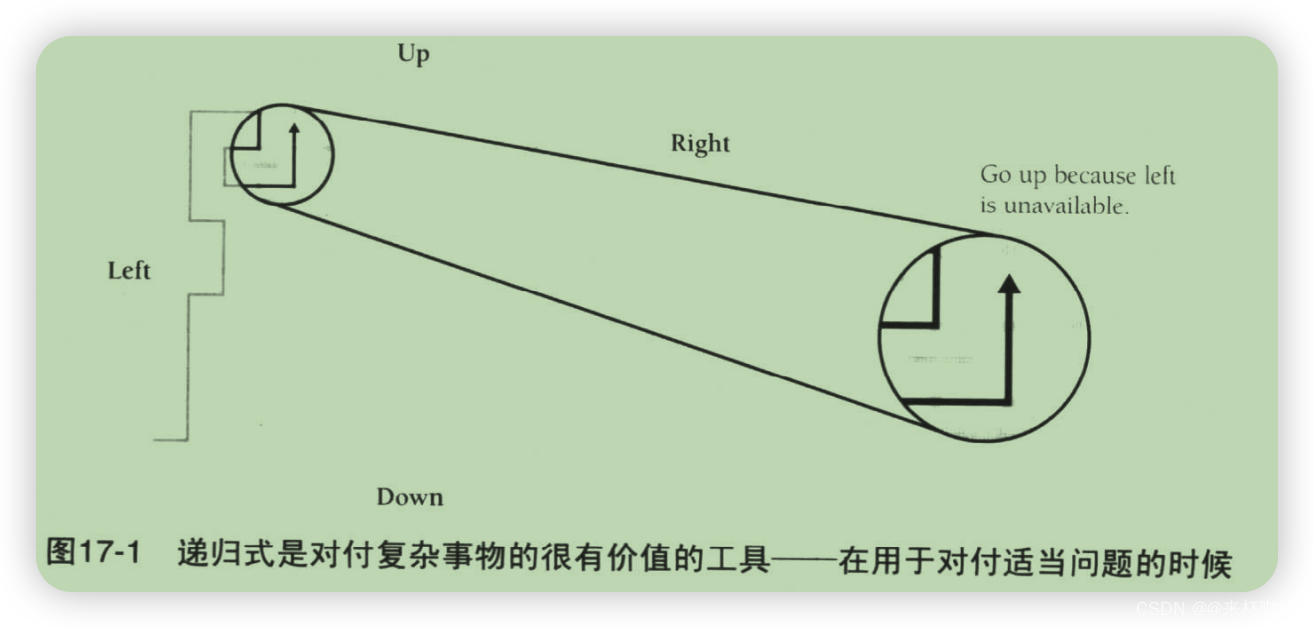
                                                 具体代码+分析，此处省略。

        这个子程序的逻辑是简单易懂的。大多数人在刚开始使用递归的时候会感到不适应，就是因为递归里的自我引用。不过，对于这个例子，使用其他的替换方案会更加复杂，而递归却能工作得非常好。

17.2.2 使用递归的技巧

        确认递归能够停止 。 检查子程序以确认其中含有一条非递归的路径。通常这意味着该子程序中含有一项判断，无须进一步递归就能停下来。在那个迷宫的例子里，AlreadyTried() 和 ThisIsTheExit(）两项判断保证递归能够停止。
        使用安全计数器防止出现无穷递归。 如果你在一种不允许使用上述简单测试的环境中使用递归，那么就用安全计数器来防止产生无穷递归。该安全计数器必须是一个不随每次子程序调用而重新创建的变量。可以用一个类成员变量，或者把该安全计数器作为参数加以传递。如下所示：

         在这个例子中，如果对子程序的调用次数超出了安全上限，递归就会停止。
        如果你不希望把安全计数器作为明确的参数传递，那么你可以使用 C++、Java或者 Visual Basic 中的成员变量，或者其他语言中的等价物。
        把递归限制在一个子程序内。 循环递归（A调用 B, B调用C，C调用A）非常危险，因为它很难检查。依靠脑力来管理位于一个子程序内的递归已经够困难了；理解跨越多个子程序的递归实在是勉为其难。如果你有循环递归，那么通常你可以重新设计这些子程序，以便把递归限制在一个单一的子程序内。如果你做不到这一点，并且仍然认为原来的递归是最好的解决方案，那么作为一种保险的递归策略，就请使用安全计数器吧。

        不要用递归去计算阶乘或者斐波纳契数列。  在计算机科学教科书中存在着这样的缺陷，那就是用愚蠢的例子来讲解递归。典型的例子就是计算阶乘或者斐波纳契数列。递归是一种强有力的工具，但是把它用在这两者中的任何一种都是愚蠢之极的。如果为我工作的程序员用递归去计算阶乘，那么我宁愿换人。下面是用递归去计算阶乘的子程序：

        除了速度缓慢，并且无法预测运行期间的内存使用状况以外，用递归写出的子程序要比用循环写出的子程序更难理解。下面就是用循环写出的子程序： 

从这个例子中可以总结出三点经验。

1. 首先，计算机科学教程中给出的递归示例没有给这个世界带来任何的好处。
2. 其次，也是更为重要的，递归是一种非常强大的工具，其功能之强大要远远超出使用它们来稀里糊涂地计算阶乘或者斐波纳契数列。
3. 再次，也是最重要的，在用递归之前你应该考虑它的替换方案。你用递归能做到的，同样也可以用栈和循环来做到。有时候用这种方法好；有时用另一种方法好。在你定下来使用哪种方法之前，请把两者都考虑一下。

17.3 goto

略。

17.4 针对不常见控制结构的观点

略。

核对表：不常见的控制结构

return

• 每一个子程序都仅在有必要的时候才使用 return 吗？
• 使用 retum 有助于增强可读性吗？

递归

• 递归子程序中包含了停止递归的代码吗？
• 子程序用安全计数器来确保该子程序能停下来吗？
• 递归只位于一个子程序里面吗？
• 子程序的递归深度处于程序栈容量可以满足的限度内吗？
• 递归是实现子程序的最佳方法吗？它要好于简单的迭代吗？