Leetcode-669. 修剪二叉搜索树

链接

669. 修剪二叉搜索树

题目

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例

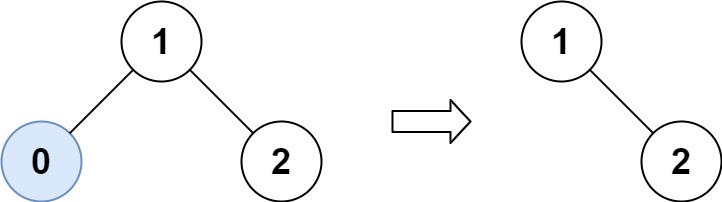
示例 1：
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]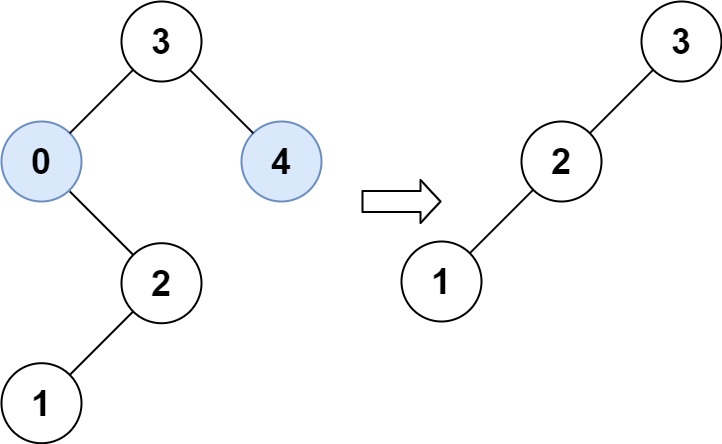

示例 2：
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

说明

• 树中节点数在范围 [1, 10e4] 内
• 0 <= Node.val <= 10e4
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 10e4

思路

我们知道，对于二叉搜索树树，若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值。因此，对于每个结点，如果该结点的左孩子的值小于low，那么整个左子树必然都小于low，直接全部剔除即可，而对于右孩子，同样地，如果值大于high，那么整个右子树可以全部剔除。而如果根节点的值在范围内，则需要对左右子树进一步递归判断。

Java Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root==null) return null;
        else if(root.val
            return trimBST(root.right,low,high);
        }
        else if(root.val>high){
            return trimBST(root.left,low,high);
        }
        else {
            root.left = trimBST(root.left,low,high);
            root.right = trimBST(root.right,low,high);
            return root;
        }
        
    }
}