统计学考研笔记：季度指数

​
        季节指数是以时间序列含有季节性周期变动的特征，计算描述该变动的季节变动指数的方法。
        统计中的季节指数预测法就是根据时间序列中的数据资料所呈现的季节变动规律性，对预测目标未来状况作出预测的方法。

长期趋势:受事物内在根本原因影响,多年内呈现持续增加或减少的总趋势。

季节变动:受自然因素、风俗习惯、社会及政治经济等因素的影响,现象在一年内呈现周期性波动。

循环波动:以若干年为周期的波动,周期为多年,但不如季节变动规律性强。(1分)

直接平均季节指数法

1. 求出各年同月或同季观察值的平均数（用A表示）。
2. 求历年间所有月份或季度的平均值（用B表示）。
3. 计算各月或各季度的季节指数，即C=A/B。

移动平均趋势剔除法

移动平均趋势剔除法是在考虑长期趋势因素影响的情况下，利用移动平均法先消除原时间数列中的长期趋势的影响，然后再测定季节变动的方法，具体计算步骤如下。

（1）根据时间数列中各季（月）的数值计算移动平均数，（若是季度资料则进行4项移动平均，若是月资料则进行12项移动平均），由于移动项数是偶数，要进行两次移动平均来求得趋势值。

（2）将时间数列中各季（月）的数值（y）与其相对应的趋势值（yc）进行对比，计算y/yc的百分比数值。

（3）把y/yc的百分比数值按季（月）排列，计算出各年同季（月）的平均数，这个平均数就是各季（月）的季节比率，即季节指数。

（4）把各季（月）的季节比率加计汇总，其总计数应等于400%（1200%），如果不符，则要进行相应的调整。

长期趋势测定

• 移动平均法

循环波动测定

• 直接法

  • 将每年各月(或季)数值与上一年同期数值对比，所求得的年距发展速度序列大体可消除长期趋势和季节变动
  • 将每年各月(或季度)数值较上年同期增长部分除以前一年对应月份(或季度)数值，得出的年距增长速度序列也可以大致消除长期趋势和季节变动，表示循环变动

• 剩余法(分解法)

1. 从序列中分别分解出长期趋势和季节变动，然后再消除不规则变动成分，剩余的变动则揭示出序列的循环变动特征。

2. 如果原序列的因素组合为Y=T·S·C·I，可以先分别消除已经分解出的季节变动S和长期趋势T，或者可以同时消除季节变动S和长期趋势T，即Y/T·S=T·C·S·I/T·S=C·I

3. 最后将所得循环变动和不规则变动的结果C·I进行移动平均，消除不规则变动I，即得循环变动值C。

题1

某超市连续4年的销售情况如下表

1. 说明具有长期趋势和循环波动
2. 请按季平均法计算各季度的季节指数。

答（1）

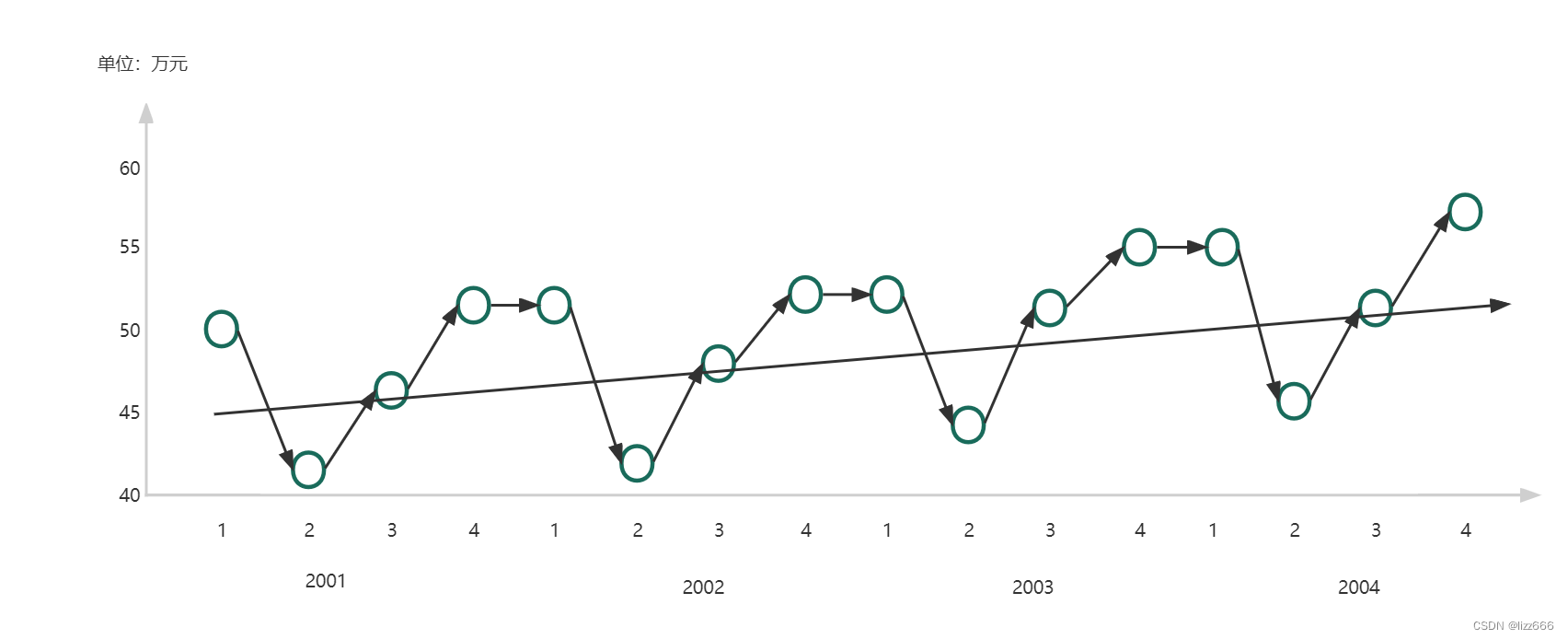
据图可知该数据具有长期趋势和循环波动。

答（2）

1. 季节指数 = 每一季的平均值/总平均值
2. Y1 = (50 + 53 + 54 + 55) / 4= 212 / 4 = 53
3. Y2 = (42 + 43 + 45 + 46) / 4 = 176 / 4 = 44
4. Y3 = (46 + 47 + 49 + 50) / 4 = 192 / 4 = 48
5. Y4 = (53 + 54 + 55 + 58) / 4 = 220 / 4 = 55
6. M = (53 + 44 + 48 + 55) / 4 = 200 /4 = 50
7. 季节指数Q1 =  Y1 / M = 53 / 50 = 1.06
8. 季节指数Q2 =  Y2 / M = 44 / 50 = 0.88
9. 季节指数Q3 =  Y3 / M = 48 / 50 = 0.96
10. 季节指数Q4 =  Y4 / M = 55 / 50 = 1.1

平均趋势剔除法：

1. 求每4个值的移动平均值，y1= (50 + 42 + 46 + 53) / 4= 47.75
2. y2= (42 + 46 + 53 + 53 ) / 4= 48.5
3. y3= (46 + 53 + 53 + 43 ) / 4= 48.75
4. y4= (53 + 53 + 43 + 47) / 4= 49
5. y5= (53 + 43 + 47 + 54) / 4= 49.25
6. y6~y13
7. 第二次2个数的的平均值，yn1 = (y1+y2)/2 = 48.125
8. yn2 = (y2+y3)/2 = 48.625
9. yn3~yn12
10. 对于的季节比率=季节值/滑动平均值，s = Y / yn 
11. s1 = Y3 / y1 = 46 / 48.125 = 95.58%
12. s2 = Y4 / y2 = 53 / 48.625 = 109%
13. s3~s12

14. 	2001年	2002年	2003年	2004年
    1季度	-	s3	s7	s11
    2季度	-	s4	s8	s12
    3季度	s1	s5	s9	-
    4季度	s2	s6	s10	-

15. 季度平均值
16. S1 = (s3+s7+s11)/3
17. S2 = (s4+s8+s11)/3
18. S3 = (s1+s5+s9)/3
19. S4 = (s2+s6+s10)/3
20. 如果 S1+S2+S3+S4 != 400% 则进行修正
21. 修正指数 x = 400/S1+S2+S3+S4
22. xS1 = S1 * x
23. xS2 = S2 * x
24. xS3 = S3 * x
25. xS4 = S4 * x

题2

1. 说明具有长期趋势和循环波动
2. 利用滑动平均趋势剔除法，求出三班制（即早、中、晚）的季节指数

答1:

答2:

1. 求每3个值的移动平均值，奇数不用进行2次平均
2. y1= (18+23+19)/3 
3. y2~y13
4. s1 = Y2/y1
5. s2~s13
6. 早中晚平均值
7. S1 ~S3
8. 如果 S1+S2+S3 != 300% 则进行修正修正指数 x = 300/S1+S2+S3
9. xS1 = S1 * x
10. xS2 = S2 * x
11. xS3 = S3 * x