AlphaGo & Model-Based RL

AlphaGo & Model-Based RL

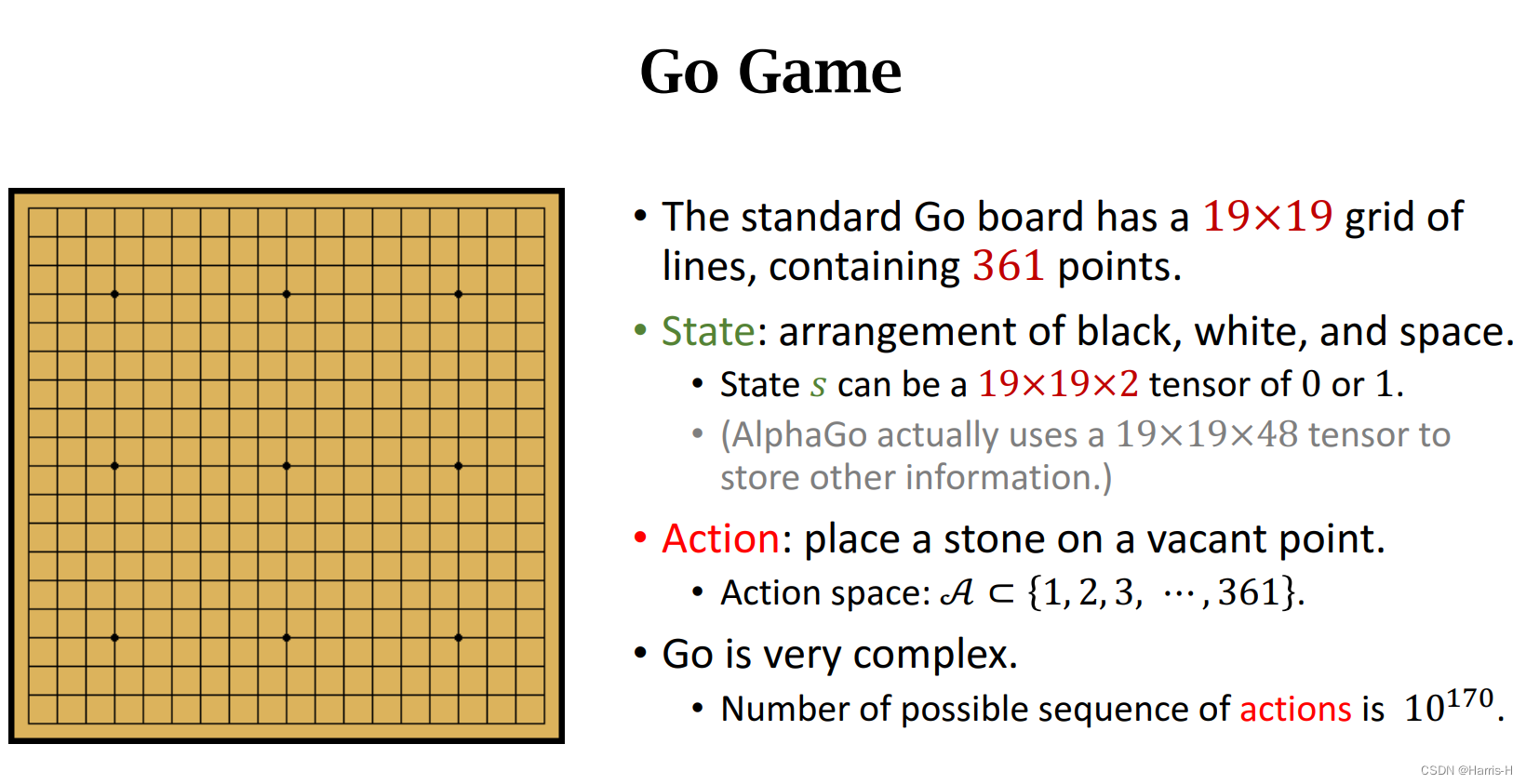
用强化学习解决围棋游戏。

---

在最初的AlphaGo 采用策略网络和价值网络，先使用behavior cloning学习人类经验训练策略网络(本质是多分类)，然后用策略梯度继续训练策略网络，再通过策略网络训练价值网络。

目前AlphaGo 采用 蒙特卡洛树搜索进行训练策略网络和价值网络。

---

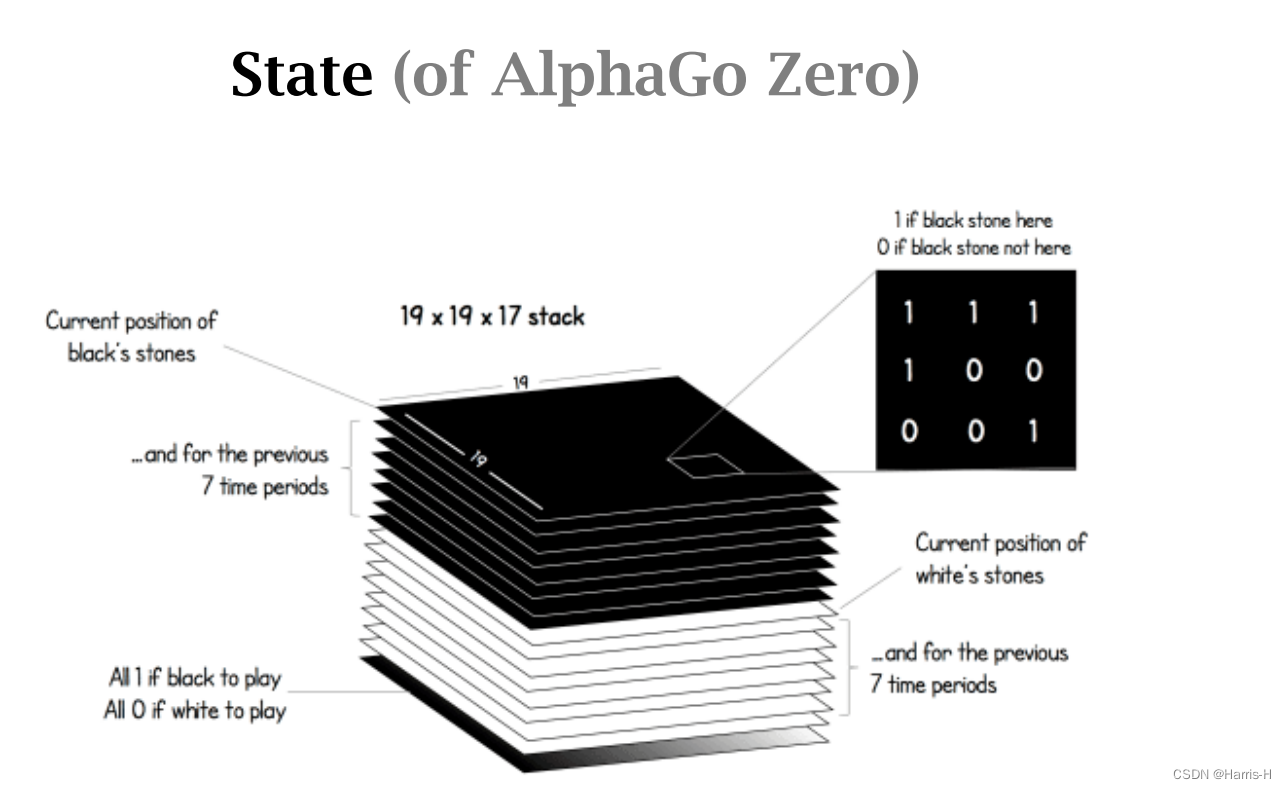
目前AlphaGo Zero使用$19\times 19\times 17$的状态，保存黑棋和白棋的最近$8$个状态，和当前是该谁走的一个状态。

---

1.策略网络

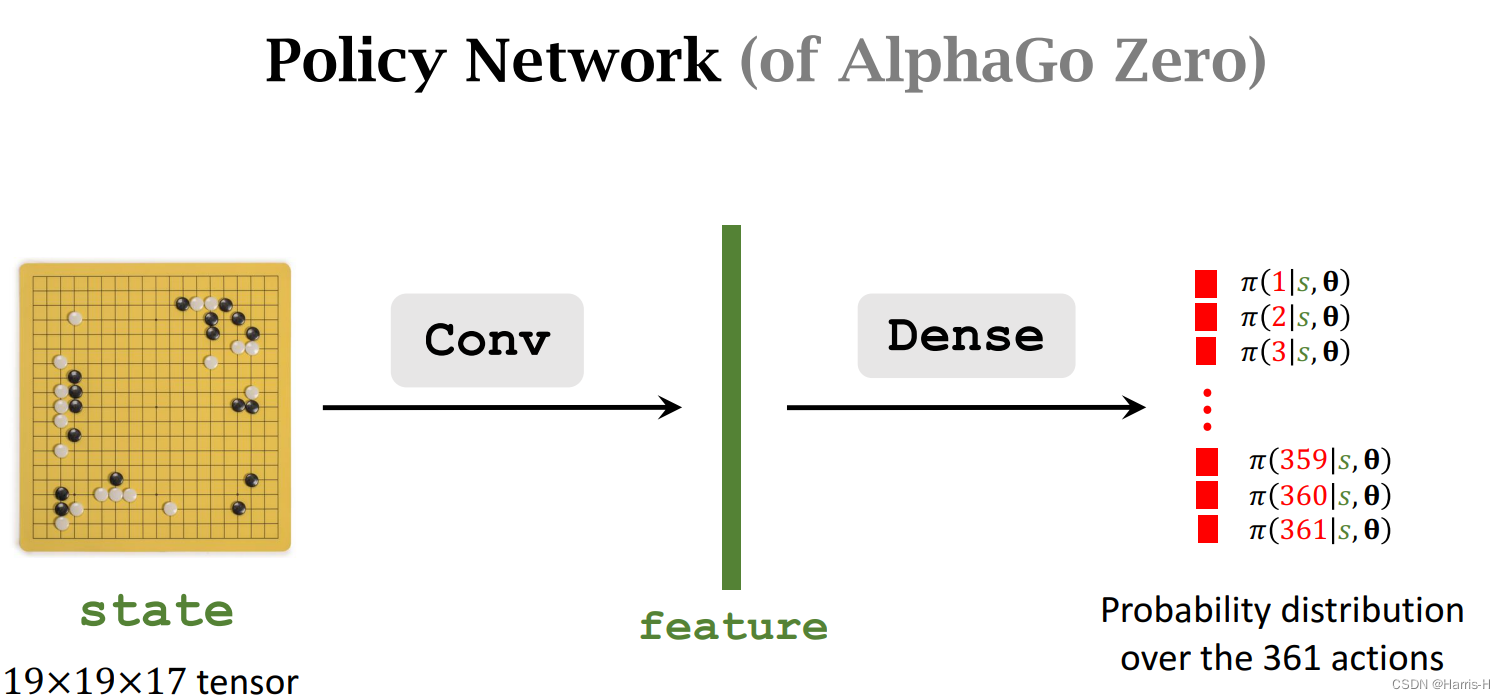
策略网络输出每个动作的概率分布。

---

2.Behavior cloning

从人类棋盘的数据集，模仿人类的经验，本质是361个类别，进行分类，不属于强化学习，而属于模仿学习。

---

---

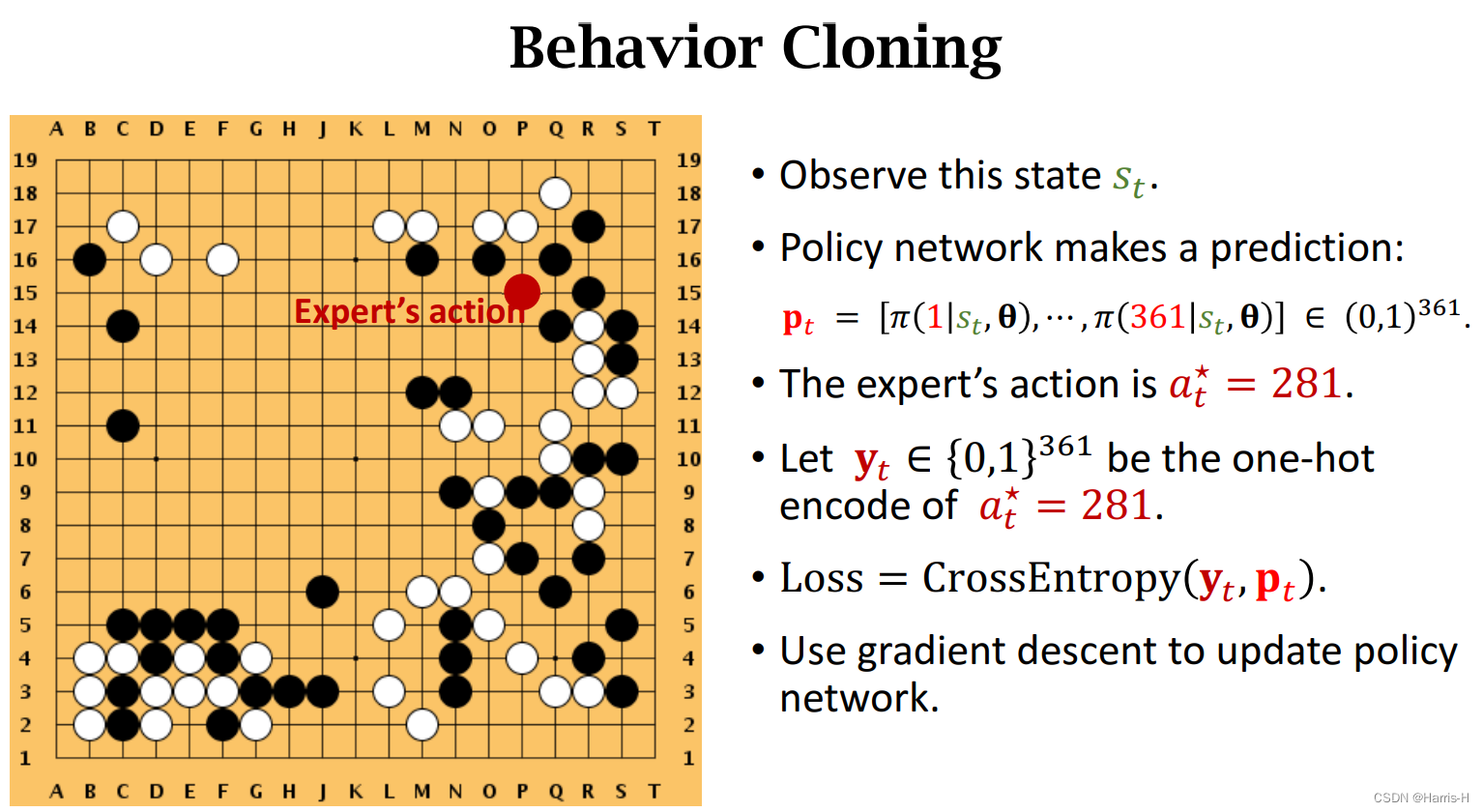
只使用便相当于6-9段的棋手，但是如果遇到在训练集中未见到的$s_t$，且状态的可能性十分巨大，动作$a_t$可能是坏的，并且这种坏的reward会不断积累，导致最终输掉。因此采用RL就非常有必要。

---

3.策略网络的强化学习

采用自我对抗的方式，Agent使用最新参数的策略网络选择动作，而对手Opponent采用策略网络的旧参数选择动作。

我们定义$r_t$为$t$时刻的奖励，$u_t$表示回报，若$r_T=1$，说明第一步到第$T$步都是好棋，所以$u_1=u_2=\cdots =u_T=1$，反之$u_1=u_2=\cdots =u_T=-1$

---

然后采用策略梯度上升更新参数$\theta$

---

---

4.价值网络

这里的价值网络近似的是$V_{\pi }(s)$函数，与之前的actor-critic算法里不同。

也就是$U_t$的期望，用来表示在策略$\pi$下，状态$s$的胜率。

---

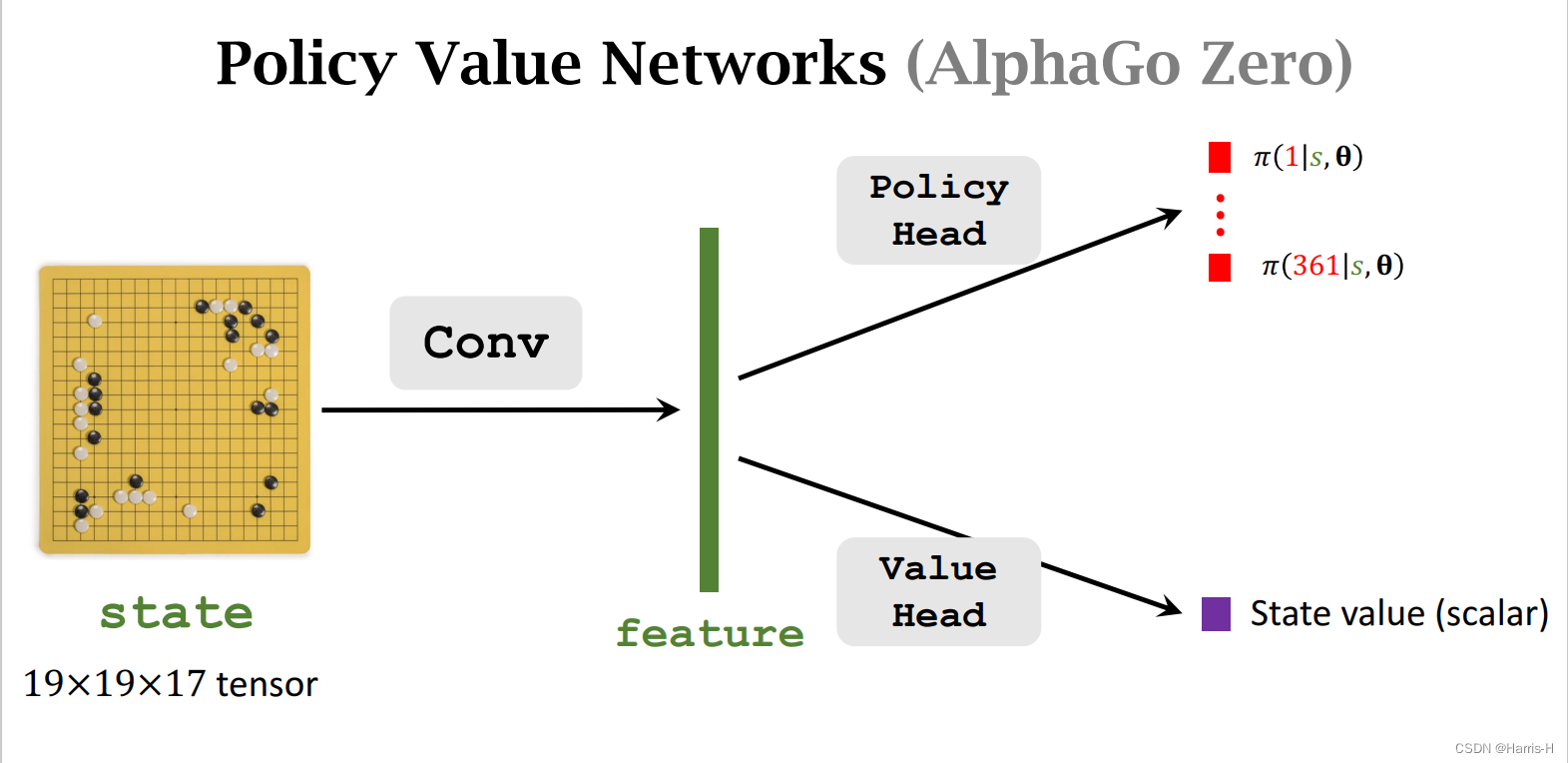
因为两个网络的相似，因此卷积层可以共用。

---

采用梯度下降更新$w$。

---

5.蒙特卡洛树搜索

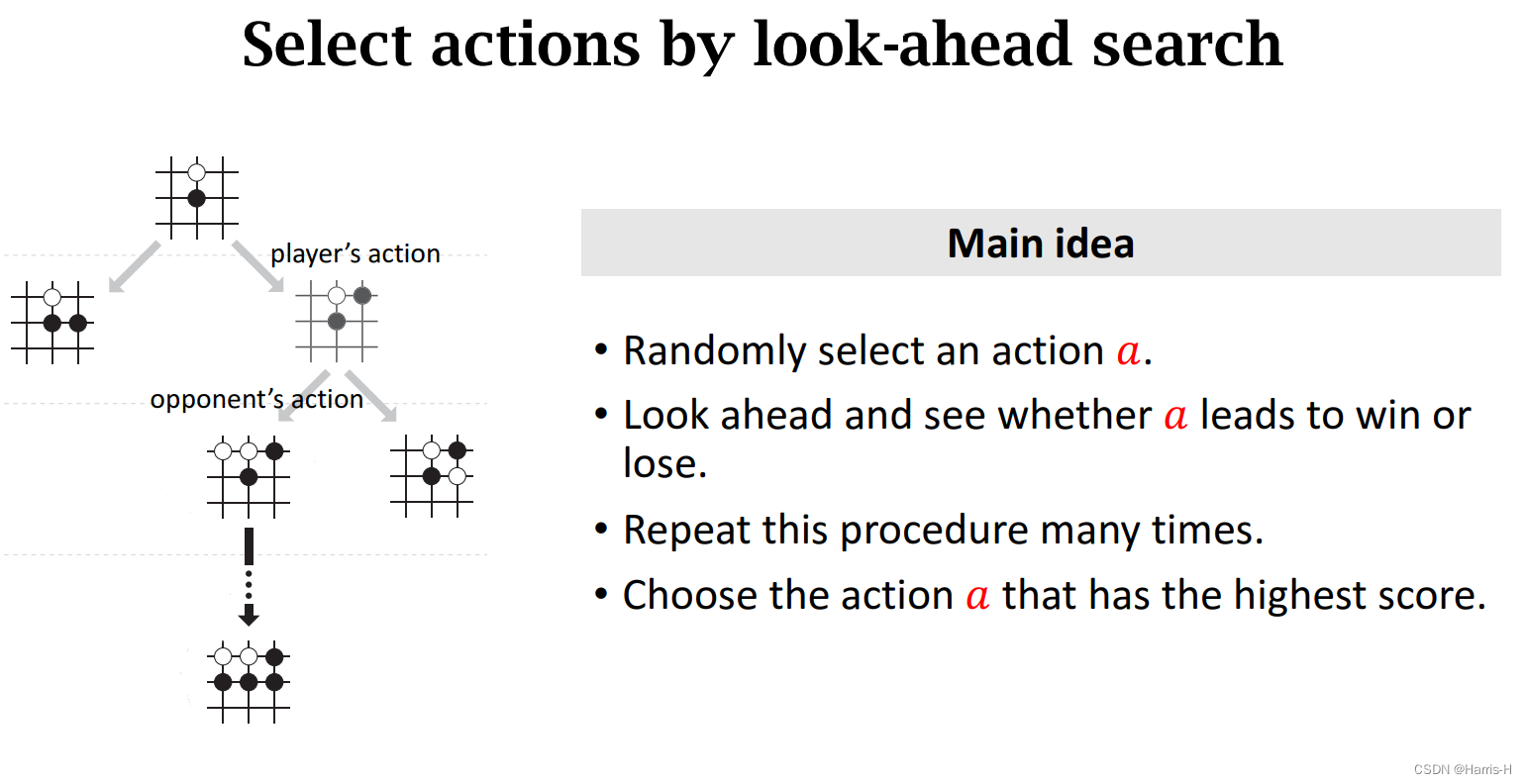
根据策略函数选取若干个较优的$a$，然后采用树搜索，类似$dfs$，进行自我对抗直到结束，然后重复多次。给每个动作$a$打分，选取打分最高的执行动作$a$。

---

具体步骤如上。

---

注意这里由$MCTS$计算的$Q(a)$是一张表，叫做动作价值表，组成每个动作打分的一部分。

$N(a)$表示动作$a$至今执行的次数。

统计完所有的动作的打分。

选择打分最大的动作，假装执行。

然后进行自我对抗，不断假想执行动作。

---

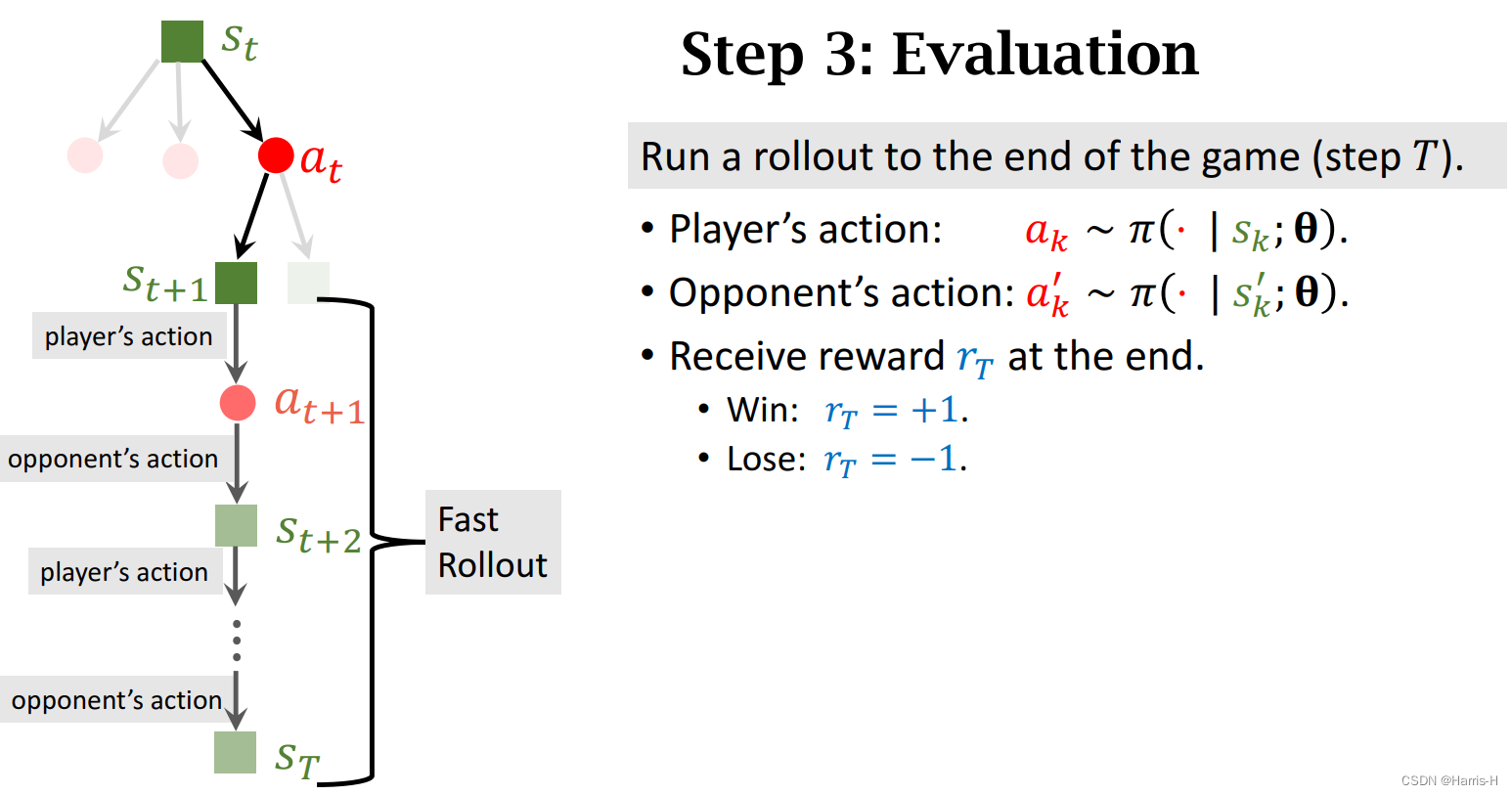
然后计算奖励$r_T$

---

然后计算$V(s_{t+1})$ ，等于价值网络输出和奖励$r_T$的均值。

---

注意每个动作存在多个$V(s_{t+1})$，因此我们采用平均值表示动作的价值$Q(a_t)$

---

然后根据$N(a)$选择最大实际执行该动作。

---

MCTS总结

---

6.新版的AlphaGo Zero

与老版本不同的时，完全不依赖于人类经验，并且在策略网络也是用MCTS训练。

---

事实证明， 人类经验对于AlphaGo的学习有副作用。

但是不能说人类经验对任何学习都无用，比如在医疗和自动驾驶方向，采用behavior cloning节省大量成本，不需要真实实验，避免不必要的危险和码分。

---

Zero策略网络的训练方法