力扣（518.377）补7.31

518.零钱兑换问题‖

我做成了排列问题，本质是组合问题。

我一开始也没想明白，这dp题真的是看起来简单，做起来难。

对于dp（k）（i）有两种可能，一是一直没有第k个硬币，二是有第k个硬币（之前可能也有第k个硬币）。这个递推式可真抽象。

int change(int amount, int* coins, int coinsSize){

    int dp[coinsSize+1][amount+1];

    memset(dp,0,sizeof(dp));

    for(int i=1;i<=coinsSize;i++)

    dp[i][0]=1;

    for(int i=1;i<=coinsSize;i++){

        for(int j=1;j<=amount;j++){

            if(j>=coins[i-1])

这里第i个硬币对应下标i-1，容易错。

            dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]];

            else dp[i][j]=dp[i-1][j];

        }

    }

    return dp[coinsSize][amount];

 

}

 

377.组合总和Ⅳ

最近排列和组合问题搞得头很疼。

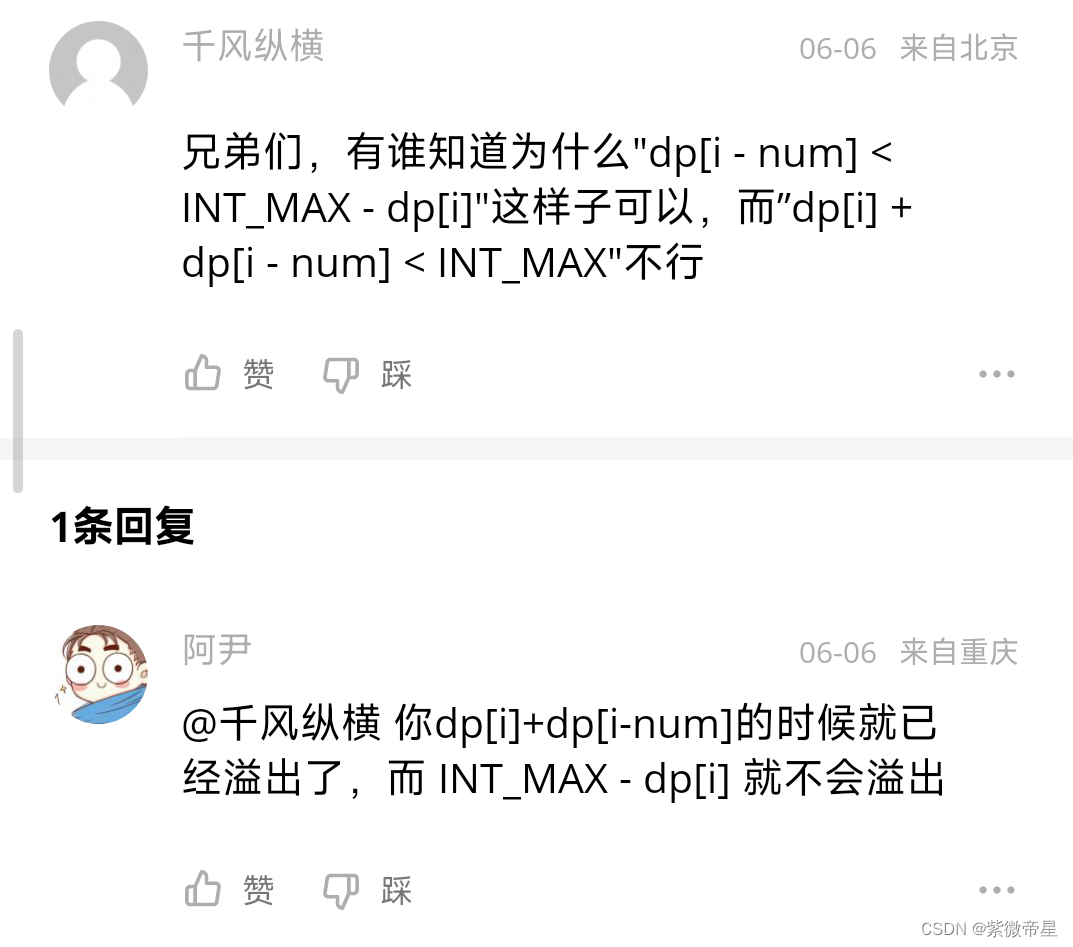
因为dp数组是把每个下标的值都求出来，不一定是递增的数组，eg：可能dp（4）越界，但dp（5）没越界，且dp（5）不是由dp（4）推出来的。

如果某个dp元素越界了，根据题目，dp（target）一定与它无关，直接跳过就行。

int combinationSum4(int* nums, int numsSize, int target){

    int dp[target+1];

    memset(dp,0,sizeof(dp));

    dp[0]=1;

    for(int i=1;i<=target;i++){

        for(int j=0;j

            if(i>=nums[j]&&dp[i]

            dp[i]+=dp[i-nums[j]];

        }

    }

    return dp[target];

 

}