• NR 物理层编码 S2 - 线性码

    参考：

    2.线性分组码-码距_哔哩哔哩_bilibili

    这里主要增加了 pyhton部分 

    目录

        

        1:    码距

        2： 线性分组码性质

        3： 纠错检错能力

        4:   生成矩阵和监督矩阵

        5： 伴随式和校正子

     

      

       

    一  码距

         

      码距

               许用码字之间的距离称为码字

      汉明距离

               两个n元码字两者之间的汉明距离为D

               码字1： w_1=a_{n-1}a_{n-2}...a_1a_0

               码字2:    w_2= b_{n-1}b_{n-2}..b_1b_0

                D(w_1,w_2)=\sum_{i}^{n}(a_i+b_i)

    二  线性分组码性质

     1.1  重要定义 

       1.2 重要性质

               自反性   

                比如 w_1+w_1=0

               对称性

                     w_1+w_2=w_2+w_1

               三角不等式

                  比如码字 w_1,w_2,w_3

                  D(w_1,w_2)+D(w_2,w_3)>D(w_1,w_3)

               

    1. # -*- coding: utf-8 -*-
    2. """
    3. Created on Tue Sep  6 11:11:40 2022
    5. @author: chengxf2
    6. """
    7. import torch
    8.  
    9. '''
    10. 求汉明距离
    11. args
    12.   w1: 许用码字1
    13.   w2: 需用码字2 
    14. '''
    15. def module(w1,w2):
    16.     
    17.     w1 = torch.ByteTensor(w1)
    18.     w2 = torch.ByteTensor(w2)
    19.     num = w1.shape[0]
    20.     dist = 0
    21.     for index in range(num):
    22.         a = w1[index]
    23.         b = w2[index]  
    24.         c =a^b
    25.         if c>0:
    26.             dist = dist+1
    27.  
    28.     print("\n 汉明距离 :",dist)
    29.     
    30. w1 = [1,1,0]
    31. w2=  [1,0,1]
    32. module(w1,w2)

    三  纠错和检错能力

          3.1  若线性分组码能检测出任一码字中的小于等于r位错误，则应满足

                d_{min}\geq \bigl(\begin{smallmatrix} r+1 \end{smallmatrix}\bigr)

                 原理：

                  假设发送码字为C, 发送了r位错误,满足上面条件，则接收到的码字

                  肯定就在禁用码字集合中，不属于许用码字集合。

                  如下列，最小码距为2的spc码

                 许用码字集合为

                 000 110  011 110

                 当发送110时候，接收方收到的数据有一位发送错误

                  变成了001,100 ,111 此刻都在禁用码字集合中，能够发现错误。

                   

              

         3.2 若线性分组码能纠正任一码字中小于等于t位误码，则

                     d_{min} \geq 2t+1

              纠错的原理是码距最近原则：

              

             同样如上图,当收到100的时候，出错了，但是这个时刻

    100 距离 110 ,000 码距都是1，此刻无法判断出到原码字到底是

    哪个.

        所以它的约束条件需要满足d_{min} \geq 2t+1

     这个译码设计原则需要特别注意,它有的场景和概率论里面的二项分布是冲突的.

    3.3  检错+纠错

    四    生成矩阵和监督矩阵

            

         4.1 生成矩阵

               输入的二进制bit流 用向量 u=[u_1,u_2,..u_k] 表示

               通过生成矩阵G得到码字

                c=uG 

                c=[c_1,c_2,..c_n]

                系统生成矩阵原理

                

                       G=[I,Q]  大小 [k,n]

                      I : 取原来信息,Q 主要作用监督 

                       p_1=\sum_{i=1}^{k}u_i a_{i1}

                       p_2=\sum_{i=1}^{k}u_i a_{i2}

                      .....

                     p_r=\sum_{i=1}^{k}u_i a_{ir}

                    

           4.2 校验矩阵

                    原理

                      

                      Hc^T =0

                    H=[Q^T,I_{r}]

           

                      例

     Q1 输入 u[1101] ，求输出的码字

     c=uG

        =[1101001]

    Q2：接收到的码字为[1101 010] 问是否出错

     Hc^T=[011]  

      出错

         

    五 伴随式和校正子

       5.1 架构

                    编码矩阵G(k,n),监督元长度r=n-k

      错误图样： E=[e_1,e_2,...e_n] 信道传输带来的随机噪声

     接收码字    R=C+E

     伴随式（校正子)

                   S=HR^T=H(C+E)^T

                             =HC^T+HE^T

                             =HE^T

                    为[r,1] 的向量，则对应2^r种组合，每一种组合叫做一个校正子

                     

     5.2  检错原理

             s \neq [o]_r 肯定发送错误

             s=[0]_r 不一定传输正确

              因为如果E 也是许用码字，HE^T=0

    5.3  纠错原理

                根据S的结果,查表得到E,根据E,利用下面公式推导出原来发送的码字

                C=R+E

    5.4 标准阵

        收到的信息 认为是 R=C+E

       当发生错误的时候，可以根据R的标准阵直接查表得到C,

    其中陪集首代表只有1位发生错误的错误图样

     

    七 例子：

     已知（6,3）系统编码矩阵G

         

     1:  求校验矩阵H

        H=[Q^T,I_r]

            

     2:  分析误码差错控制能力

           

         因为H中 任意两列不相同，3列线性相关，

          [110]+[101]=[011] 

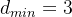          所以d_{min}=3,则

         检错能力为2， 纠错能力为1

        见程序

    3： 1位误码所有的错误图样

    见程序

        

    E[1]:  [1, 0, 0, 0, 0, 0]      错误图样  S[1]: [1, 1, 0]

     E[2]:  [0, 1, 0, 0, 0, 0]      错误图样  S[2]: [1, 0, 1]

     E[3]:  [0, 0, 1, 0, 0, 0]      错误图样  S[3]: [0, 1, 1]

     E[4]:  [0, 0, 0, 1, 0, 0]      错误图样  S[4]: [1, 0, 0]

     E[5]:  [0, 0, 0, 0, 1, 0]      错误图样  S[5]: [0, 1, 0]

     E[6]:  [0, 0, 0, 0, 0, 1]      错误图样  S[6]: [0, 0, 1]

    4   写出所有的错误图样

    1. # -*- coding: utf-8 -*-
    2. """
    3. Created on Thu Sep  8 11:04:28 2022
    5. @author: chengxf2
    6. """
    7. import numpy  as np
    8.  
    9. '''
    10. 模二加法
    11. '''
    12. def module(u,g):
    13.       n = np.dot(u,g.T)
    14.       #print("\n n: ",u,g)
    15.       return n%2
    16. '''
    17. 编码过程
    18. '''    
    19. def encode(u,G):
    20.      G = np.array(G)
    21.      u = np.array(u)
    22.      
    23.      
    24.      k,n = G.shape[0],G.shape[1]
    25.  
    26.      #print("\n k: %d  n: %d"%(k,n))
    27.      
    28.      code =[]
    29.      for index in range(n):
    30.          
    31.          g = G[:,index]
    32.          if index<k:
    33.              a = u[index]
    34.          else:
    35.              a = module(u,g)
    36.          code.append(a)
    37.      return code
    38.  
    39.  
    40. '''
    41. 译码过程
    42. '''
    43. def decode(E,H):
    44.     
    45.      E= np.array(E)
    46.      H = np.array(H)
    47.     
    48.      m,n = np.shape(H)
    49.      S =[]
    50.      for index in range(m):
    51.          
    52.          p = H[index,:]
    53.          r = module(E,p)
    54.          S.append(r)
    55.      return S
    56.  
    57.  
    58. if __name__ =="__main__":
    59.     
    60.     uList =[[0,0,0],
    61.             [0,0,1],
    62.             [0,1,0],
    63.             [1,0,0],
    64.             [0,1,1],
    65.             [1,1,0],
    66.             [1,1,1]]
    67.     
    68.     G = [[1,0,0,1,1,0],
    69.          [0,1,0,1,0,1],
    70.          [0,0,1,0,1,1]]
    71.     
    72.     H = [[1,1,0,1,0,0],
    73.          [1,0,1,0,1,0],
    74.          [0,1,1,0,0,1]]
    75.     for u in uList:
    76.         code =encode(u,G)
    77.         print("\n 信息: ",u,"\t 输出码字: ",code)
    78.         
    79.         
    80.     EList =[[1,0,0,0,0,0],
    81.             [0,1,0,0,0,0],
    82.             [0,0,1,0,0,0],
    83.             [0,0,0,1,0,0],
    84.             [0,0,0,0,1,0],
    85.             [0,0,0,0,0,1]]
    86.     
    87.     for E in EList:
    88.         
    89.         S =decode(E,H)
    90.         print("\n E, ",E,"\t S",S)

     4  假设收到的码字为[001110],求正确码字为

       S=HR^T

            =[1,0,1]

      查表得到E

           E[2]:  [0, 1, 0, 0, 0, 0]      错误图样  S[2]: [1, 0, 1]

       C=R+E

         =[0,1,0,0,0,0]+[0,0,1,1,1,0]

         =[0,1,1,1,1,0]

  • 相关阅读:
    提升效率必备：电脑文件批量重命名的实用技巧大放送
    关于Gson的TypeToken
    领域驱动设计DDD：贫血模型和充血模型（比较重要）
    高通cDSP简单编程例子（实现查询高通cDSP使用率、签名），RK3588 npu使用率查询
    文字识别ORC与公式识别
    用前端写桌面应用
    Qt实现手动切换多种布局
    go-mysql-elasticsearch 使用
    Android Frgment中onActivityResult无效的问题
    Tomcat部署
  • 原文地址：https://blog.csdn.net/chengxf2/article/details/126720871