数学笔记；离散傅里叶变化 DFT

数学笔记；离散傅里叶变化 DFT
1 原理介绍
- 离散傅里叶变化是连续傅里叶变化在如下信号下的等价形式：
  - N个样本
  - 每个样本的采样间隔是T
- 令f(t)是数据源的持续信号，将N个样本表示成f[0],f[1],f[2],.....f[k],....f[N-1]
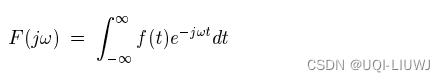
  - ——>原始数据源信号f(t)的傅里叶变换，应该是
- 因为信号脉冲仅在样本点采集，所以可以如下近似：
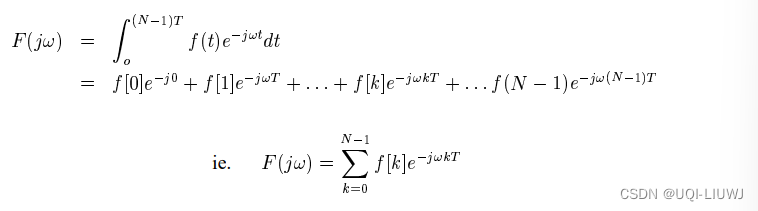
- 这里，DFT假设波形是周期性的（周期正好是T个interval的跨度）
  - 也就是这里我们是从0到N-1采样的f(0)到f(N-1)，和从N到2N-1采样得到的f(N)到f(2N-1)是一样的
  - 比如我们采样了10个点（0~10），那么DFT会隐式地人为周期就是10
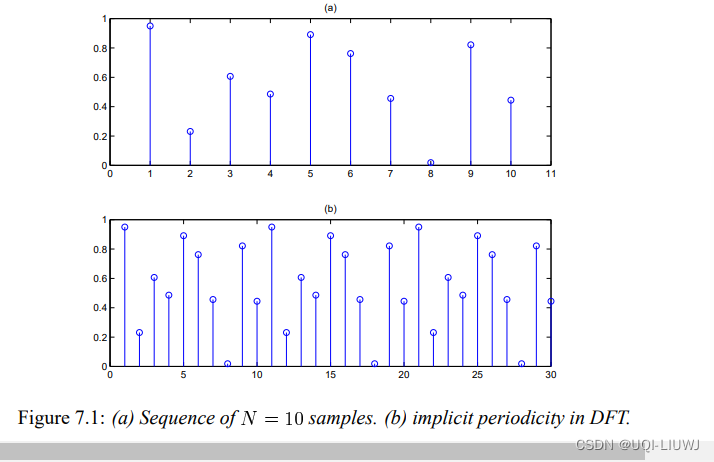
- 所以上式中的ω被表示为：
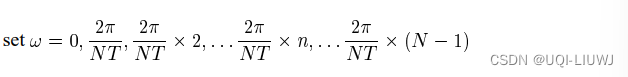
- 所以离散傅里叶级数可以表示为：
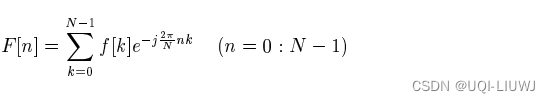
- 上式可以被重写成：
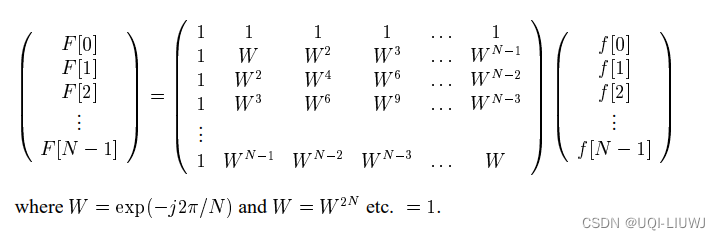
1.1 欧拉公式（复习）

2 举例

令连续信号为： $f[k]=5+2cos(\frac{\pi}{2}k-90^\cdot)+3cos(4\pi t)$

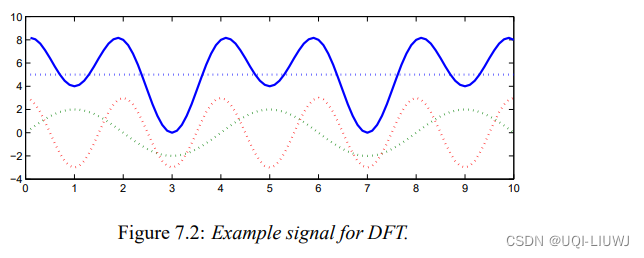
采样k=0~k=3 四个点，得到f[0]=8,f[1]=4,f[2]=8,f[3]=0

于是

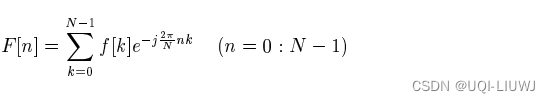
可以写成：

$F[n]=\sum_{k=0}^3 f[k] e^{-j \frac{2\pi}{4}kn}=\sum_{k=0}^3 f[k] (-j)^{kn}$

用矩阵的形式，可以写成

$\begin{bmatrix} F[0]]\\ F[1]\\ F[2]\\ F[3] \end{bmatrix} =\begin{bmatrix} 1 & 1 & 1 & 1\\ (-j)^0 &(-j)^1 &(-j)^2 &(-j)^3 \\ [(-j)^2]^0 & [(-j)^2]^1 & [(-j)^2]^2 & [(-j)^2]^3 \\ [(-j)^3]^0 & [(-j)^3]^1 & [(-j)^3]^2 & [(-j)^3]^3 \end{bmatrix} \begin{bmatrix} f[0]\\ f[1]\\ f[2]\\ f[3] \end{bmatrix}$

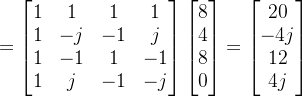
$=\begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & -j & -1 & j \\ 1 & -1 & 1 & -1 \\ 1 & j & -1 & -j \end{bmatrix} \begin{bmatrix} 8\\ 4\\ 8\\ 0\end{bmatrix} =\begin{bmatrix} 20\\ -4j\\ 12\\ 4j \end{bmatrix}$

4 逆傅里叶变化

的逆傅里叶变化是：

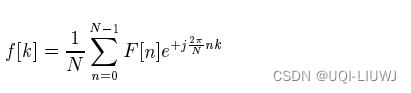
如果这里令 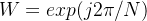$W=exp(j2\pi/N)$ 的话，那么逆傅里叶变化的矩阵形式为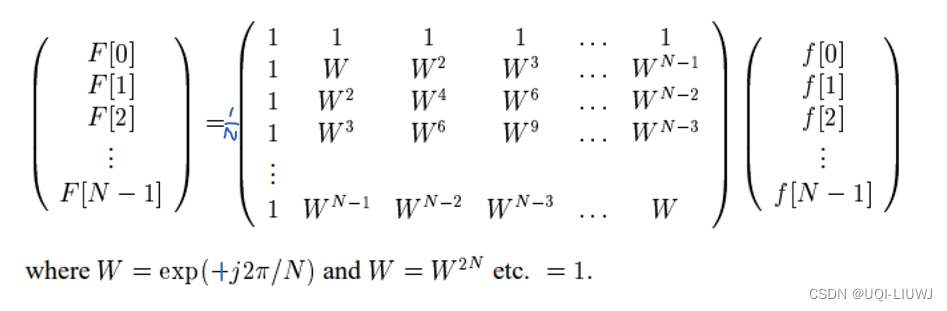

4.1 举例

还是用前面一个例子

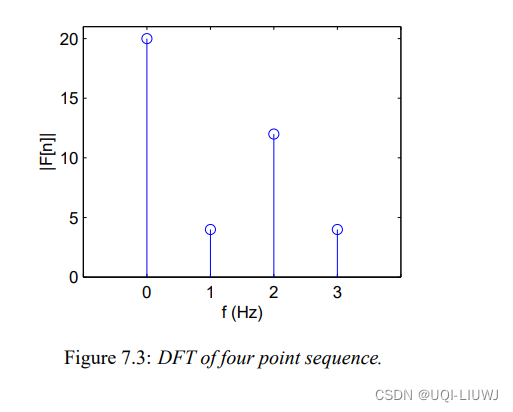
已知F[0]=20,F[1]=-4j,F[2]=12,F[3]=4j

希望得到：f[0]=8,f[1]=4,f[2]=8,f[3]=0

$\begin{bmatrix} f[0]]\\ f[1]\\ f[2]\\ f[3] \end{bmatrix} =\frac{1}{4}\begin{bmatrix} 1 & 1 & 1 & 1\\ (j)^0 &(j)^1 &(j)^2 &(j)^3 \\ [(j)^2]^0 & [(j)^2]^1 & [(j)^2]^2 & [(j)^2]^3 \\ [(j)^3]^0 & [(j)^3]^1 & [(j)^3]^2 & [(j)^3]^3 \end{bmatrix} \begin{bmatrix} F[0]\\ F[1]\\ F[2]\\ F[3] \end{bmatrix}$

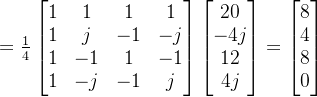
$=\frac{1}{4}\begin{bmatrix} 1 & 1 & 1 & 1\\ 1 & j & -1 & -j \\ 1 & -1 & 1 & -1 \\ 1 & -j & -1 & j \end{bmatrix} \begin{bmatrix} 20\\ -4j\\ 12\\ 4j\end{bmatrix} =\begin{bmatrix} 8\\ 4\\ 8\\ 0 \end{bmatrix}$
相关阅读:
Java面试题总结（三）
C语言入门（二）运算符和表达式
 那些年印象深刻的面试
 《大厂面试》之JVM篇21问与答
 PMP项目管理实战 | 项目经理如何做好会议管理？
解析 Python requests 库 POST 请求中的参数顺序问题
 go传统的同步机制
 数据集市简介
 Python 中的 DNS 查找
 inet_ntop4源代码实现
原文地址：https://blog.csdn.net/qq_40206371/article/details/126772853

1 原理介绍

1.1 欧拉公式 （复习）

2 举例

4 逆傅里叶变化

4.1 举例

1.1 欧拉公式（复习）