【数组】优美的排列 II

题目描述

给你两个整数 n 和 k ，请你构造一个答案列表 answer ，该列表应当包含从 1 到 n 的 n 个不同正整数，并同时满足下述条件：

假设该列表是 answer = [a1, a2, a3, ... , an] ，那么列表 [|a1 - a2|, |a2 - a3|, |a3 - a4|, ... , |an-1 - an|] 中应该有且仅有 k 个不同整数。
返回列表 answer 。如果存在多种答案，只需返回其中 任意一种 。

示例 1：

输入：n = 3, k = 1
输出：[1, 2, 3]
解释：[1, 2, 3] 包含 3 个范围在 1-3 的不同整数，并且 [1, 1] 中有且仅有 1 个不同整数：1

解题思路

这道题实际是一道数学题目，找数学规律；下面就是分析这个题目的过程：

假设n=4，分别求解k=[1,2,3]的answer列表：

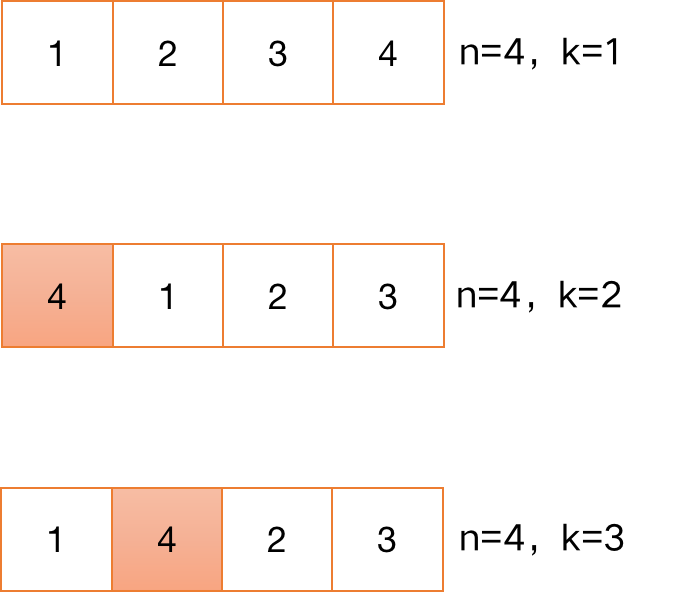
假设n=5，分别求解k=[1,2,3,4]的answer列表：

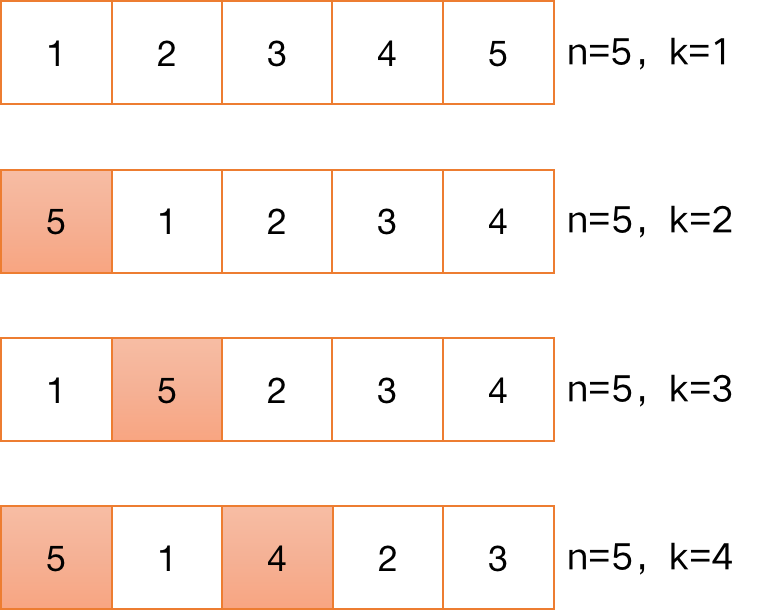
根据这个规律可以有下面的思路：

• 准备2个list，分别是l1和l2;
• 计算分割时需要的数字长度：move=k/2；
• l1记录从1到n-move的数字，l2记录从n到n-move+1的数字；
• 判断是l1的数字作为第一个，还是l2的数字作为第一个；判断逻辑如下：boolean isLeftFirst = k % 2 == 1;
• 开始merge操作，将结果merge到 int res[] = new int[n]中；
• 返回res。

---

代码实现如下：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
 
class Solution1 {
    public int[] constructArray(int n, int k) {
        int move = k / 2;
 
        int left = 1;
 
        List l1 = new ArrayList<>(n - move);
        for (int i = left; i <= n - move; i++) {
            l1.add(i);
        }
        List l2 = new ArrayList<>(move);
        for (int i = n; i > n - move; i--) {
            l2.add(i);
        }
 
        int leftIndex = 0;
        int rightIndex = 0;
        int index = 0;
        int[] res = new int[n];
 
        boolean isLeftFirst = k % 2 == 1;
 
        while (leftIndex < l1.size() && rightIndex < l2.size()) {
            if (isLeftFirst) {
                res[index] = l1.get(leftIndex);
                index++;
                leftIndex++;
                res[index] = l2.get(rightIndex);
                index++;
                rightIndex++;
            } else {
                res[index] = l2.get(rightIndex);
                index++;
                rightIndex++;
                res[index] = l1.get(leftIndex);
                index++;
                leftIndex++;
            }
        }
 
        while (leftIndex < l1.size()) {
            res[index] = l1.get(leftIndex);
            index++;
            leftIndex++;
        }
        while (rightIndex < l2.size()) {
            res[index] = l2.get(rightIndex);
            index++;
            rightIndex++;
        }
 
        return res;
    }
 
    public static void main(String[] args) {
        Solution1 solution = new Solution1();
        System.out.println(Arrays.toString(solution.constructArray(4, 1)));
        System.out.println(Arrays.toString(solution.constructArray(4, 2)));
        System.out.println(Arrays.toString(solution.constructArray(4, 3)));
 
 
        System.out.println(Arrays.toString(solution.constructArray(5, 1)));
        System.out.println(Arrays.toString(solution.constructArray(5, 2)));
        System.out.println(Arrays.toString(solution.constructArray(5, 3)));
        System.out.println(Arrays.toString(solution.constructArray(5, 4)));
    }
}

---

按照上述思路，能够解决问题，但是耗时方面还可以进一步优化；

这里不再使用l1 和 l2 做list的合并，改成直接merge数组，int res[] = new int[n]; 按照这个思路改写完成后代码如下：

 
import java.util.Arrays;
 
class Solution {
    public int[] constructArray(int n, int k) {
        int move = k / 2;
        boolean isLeftFirst = k % 2 == 1;
 
        int left = 1;
        int right = n;
        int countIndex = 0;
        int[] newRes = new int[n];
 
        while (countIndex < n) {
 
            if (isLeftFirst) {
                if (left <= n - move) {
                    newRes[countIndex] = left;
                    left++;
                    countIndex++;
                }
 
                if (right > n - move) {
                    newRes[countIndex] = right;
                    right--;
                    countIndex++;
                }
            } else {
                if (right > n - move) {
                    newRes[countIndex] = right;
                    right--;
                    countIndex++;
                }
 
                if (left <= n - move) {
                    newRes[countIndex] = left;
                    left++;
                    countIndex++;
                }
            }
        }
        return newRes;
    }
 
    public static void main(String[] args) {
        Solution solution = new Solution();
        System.out.println(Arrays.toString(solution.constructArray(4, 1)));
        System.out.println(Arrays.toString(solution.constructArray(4, 2)));
        System.out.println(Arrays.toString(solution.constructArray(4, 3)));
 
 
        System.out.println(Arrays.toString(solution.constructArray(5, 1)));
        System.out.println(Arrays.toString(solution.constructArray(5, 2)));
        System.out.println(Arrays.toString(solution.constructArray(5, 3)));
        System.out.println(Arrays.toString(solution.constructArray(5, 4)));
    }
}

 这道题优化结果如下：

总结

最近做这些题目发现都是找数学规律，找到数学规律后再做代码实现，最后是做代码耗时优化，后续可以多看看数学相关的书籍。