LeetCode 每日一题——667. 优美的排列 II

1.题目描述

667. 优美的排列 II

给你两个整数 n 和 k ，请你构造一个答案列表 answer ，该列表应当包含从 1 到 n 的 n 个不同正整数，并同时满足下述条件：

假设该列表是 answer = [a1, a2, a3, … , an] ，那么列表 [|a1 - a2|, |a2 - a3|, |a3 - a4|, … , |an-1 - an|] 中应该有且仅有 k 个不同整数。
返回列表 answer 。如果存在多种答案，只需返回其中 任意一种 。

示例 1：

输入：n = 3, k = 1
输出：[1, 2, 3]
解释：[1, 2, 3] 包含 3 个范围在 1-3 的不同整数，并且 [1, 1] 中有且仅有 1 个不同整数：1
1
2
3

示例 2：

输入：n = 3, k = 2
输出：[1, 3, 2]
解释：[1, 3, 2] 包含 3 个范围在 1-3 的不同整数，并且 [2, 1] 中有且仅有 2 个不同整数：1 和 2

2.解题思路与代码

2.1 解题思路

这是一道纯粹的找规律的题目，首先我们来看当所有数字按照默认规则排序时，相邻两个数之间的差都是 1 ，因此此时不同差值个数是 1

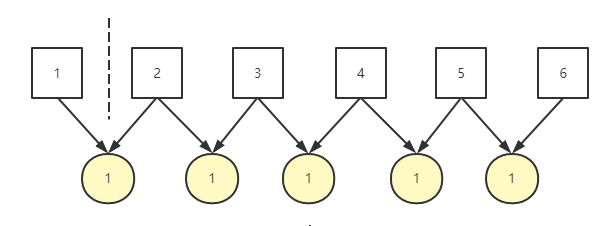
如果我们将 1 移动到 2 的前面，那么此时相邻两数差值如下，1 和 3 的差值为 2 其余差值均为 1，因此不同差值个数为 2

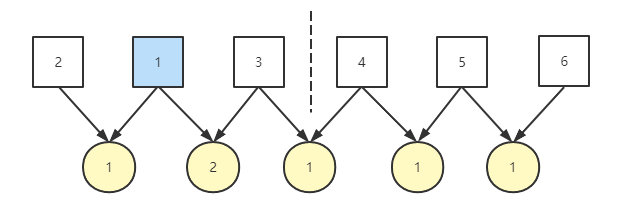
我们继续将 1 向右移动到 3 之后，此时 1 和 3 的差值为 2、1 和 4 的差值为 3，整个数列的的差值个数为 3

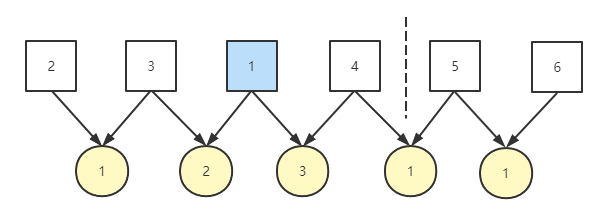
此时如果只移动 1 的话不同的差值个数也始终保持 3 个不会改变，因此需要移动一次 2 来增加不同差值个数，此时不同差值个数为 4

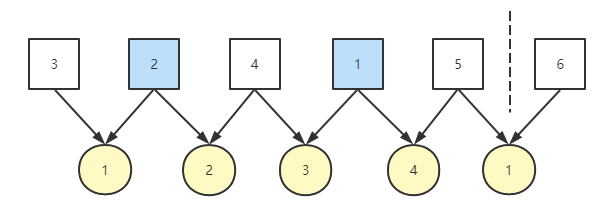
我们再次移动数列，不同差值个数便增加到了 5 个

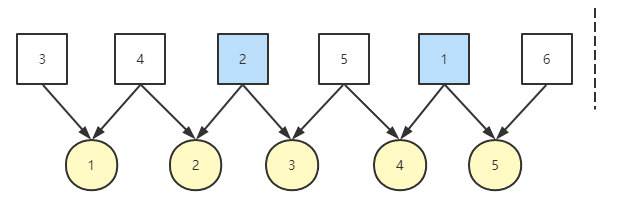
从上面我们便可以找到规律：当我们再寻在数列中 k 个不同差值时，我们就在 [1, k] 区间上对数列进行重排，第 k 个位置为 k，k-1 位置为 1，k-2 位置为 k-1，k-3 位置为2……依次类推。也就是将区间上的数从高位开始，高位和低位交替即可，k+1 位之后的位置保持吃不变，差值始终为 1。

2.2 代码

class Solution {
    public int[] constructArray(int n, int k) {
        int left = 1;
        int right = k + 1;
        int count = k;
        int step = 0;
        int[] ans = new int[n];
        // 交替存放 [0, k] 位置上的数字
        while (step <= k) {
            if (step % 2 == 0) {
                ans[count] = right;
                count--;
                right--;
            } else {
                ans[count] = left;
                count--;
                left++;
            }
            step++;
        }
        // k+1 位以后的位置保持不变，差值始终为 1
        int remain = k + 1;
        while (remain < n) {
            ans[remain] = remain + 1;
            remain++;
        }
        return ans;

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2.3 测试结果

通过测试

3.总结

• 寻找差值规律
• 在区间内交替存放高低位数字