剑指offer(C++)-JZ38：字符串的排列(算法-搜索算法)

作者：翟天保Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

题目描述：

输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。

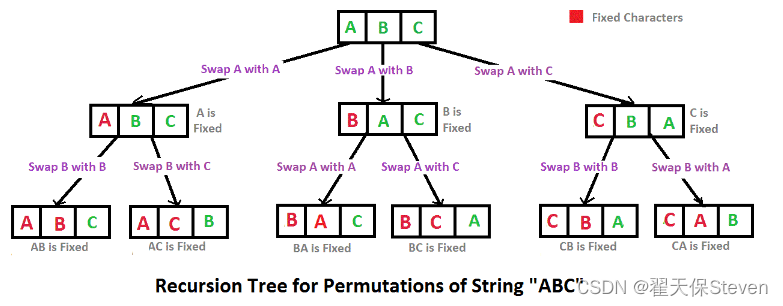
例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

数据范围：n<10
要求：空间复杂度 O(n!)，时间复杂度 O(n!)

示例：

输入：

"aab"

返回值：

["aab","aba","baa"]

解题思路：

本题考察算法-搜索算法的使用。具体实现列了三种写法：

解法一：next_permutation函数

1. 使用STL内置算法next_permutation，该函数会将字符串转换为下一排列。
2. 如果对字符串先执行了排序，再循环调用next_permutation，直至字符串反序，就相当于获得了字符串从正序到反序的全排列。

解法二：仿写next_permutation函数

1. 考虑到很多同学想要了解next_permutation的原理逻辑，进行了仿写，仅供参考。
2. 通过for循环，使得i最终位置是从右到左的首个正序的起始点。
3. 若i小于0，说明此时字符串已是反序，全排序已完毕。
4. 再通过for循环，找到比i大的字符中最小的那个，i和j交换，这样可满足字典序的全排列顺序。
5. i和j交换后，i后面的字符串应该是反序状态，将其反转为正序，再继续找新的排列。

解法三：深度优先遍历DFS

1. 先字典序排序，再进行深度优先遍历获取全排列，用递归实现。
2. 当临时字符串尺寸与输入字符串尺寸一致时，递归返回，并将当前字符串存入数组。
3. 通过for循环，遍历所有元素，当某字符被加入到字符串了，就跳过该字符；当前的字符如果同前一个字符相同，且前面的字符还没用过，也跳过，不然会重复获取相同的字符串。
4. 被加入的字符，将vis数组对应位置设1，作标记用，并将其加入临时字符串中。
5. 某深度遍历完毕后，回溯到上一层，换不同的组合得到新的排列。
6. 以此类推，直到所有的排列获取。

测试代码：

解法一：next_permutation函数

class Solution {
public:
    vector<string> Permutation(string str) 
    {
        vector<string> ans;
        // 判空
        if (str.empty()) 
            return ans;
        // 排序
        sort(str.begin(), str.end());
        // 全排列，next_permutation会将str转为下一个排列
        do {
            ans.push_back(str);
        } while (next_permutation(str.begin(), str.end()));
        return ans;
    }    
};

解法二：仿写next_permutation函数

class Solution {
public:
    vector<string> Permutation(string str) 
    {
        vector<string> ans;
        // 判空
        if(str.size() == 0)
            return ans;
        // 排序
        sort(str.begin(),str.end());
        // 全排列
        do {
            ans.push_back(str);
        } while (nextPermutation(str));
        return ans;
    }
    
    // 变换为下个排列
    bool nextPermutation(string &str) 
    {
        // len为字符串长度
        int len = str.size();
        // 通过for循环，使得i最终位置是从右向左的首个正序的起始点
        int i = len-2;
        for(;i>=0 && str[i]>=str[i+1];i--);
        // 若i小于0，说明此时字符串已是反序，全排列已完毕
        if(i < 0 )
            return false;
        // 通过for循环，找到比i大的字符中最小的那个，i和j交换
        // 交换后，i后面的字符串应该是反序状态
        int j = len-1;
        for(;j>=0 && str[j]<=str[i];j--);
        char temp = str[i];
        str[i] = str[j];
        str[j] = temp;
        // 将i后面的字符串反转成正序，继续找新的排列
        for(int a = i+1,b = len-1;a < b;a++,b--)
        {
            temp = str[a];
            str[a] = str[b];
            str[b] = temp;
        }
        return true;
    }
};

解法三：深度优先遍历DFS

class Solution {
public:
    // 深度优先遍历
    void DFS(vector<string> &res, string &str, string &temp, vector<int> &vis)
    {
        // 临时字符串满了加入输出
        if(temp.length() == str.length())
        { 
            res.push_back(temp);
            return;
        }
        // 遍历所有字符选取一个加入
        for(int i = 0; i < str.length(); i++)
        { 
            // 如果该字符已经被加入了则不需要再加入了
            if(vis[i]) 
                continue;
            // 当前的字符str[i]与同一层的前一个字符str[i-1]相同且str[i-1]还没用过，则跳过，避免重复
            if(i > 0 && str[i - 1] == str[i] && !vis[i - 1])
                continue;
            // 标记为使用过  
            vis[i] = 1;  
            // 加入临时字符串
            temp.push_back(str[i]); 
            // 深度优先遍历
            DFS(res, str, temp, vis);
            // 回溯
            vis[i] = 0; 
            temp.pop_back();
        }
    }
    
    vector<string> Permutation(string str) 
    {
        // 先按字典序排序，使重复字符串相邻
        sort(str.begin(), str.end()); 
        // 标记每个位置的字符是否被使用过s
        vector<int> vis(str.size(), 0); 
        vector<string> res;
        string temp;
        // 深度优先遍历
        DFS(res, str, temp, vis); 
        return res;
    }
};