【论文阅读】SSC: Semantic Scan Context for Large-Scale Place Recognition

一、系统概述

这篇文章是浙江大学发表的一个结合语义的描述子编码方法，主要是对之前看过的A-LOAM里面增加的回环检测方法，也就是Scan Context做了改进，主要是向里面增加了语义的信息。

在这篇论文中，作者提出了分两步的全局的语义ICP和语义的Scan Context描述子，在全局的语义ICP中又拆分为了两部分：快速偏航角计算以及快速的语义ICP匹配。对于一帧点云，用三维坐标加上语义标签四个量来表示其中的每个点，对于检验回环的场景，首先利用两帧电晕计算一个全局旋转角，将两帧点云角度对齐，再利用ICP的方法计算一个平面偏移，得到的平面偏移将点云做叠加，最后再用描述子做匹配，得到的相似度分数就用来判断是不是真的出现了回环。

二、全局语义ICP

ICP本身是一个迭代优化的过程，一旦陷入局部最优值就很难迭代出来，并且合适的初值也很重要，针对于初值和局部最优值的问题，这篇论文提出了全局语义ICP的解决方法，这个方法分为两步：快速偏航角计算以及快速语义ICP计算。

快速偏航角计算

传统的Scan Context描述子因为它环形的编码方法，不具有旋转不变性，这导致编码出来的二维矩阵在匹配时，必须要不断调整列来找出最优的角度，可以说是开销大而且有些暴力。在这篇论文中，论文没有提用的什么网络来获取语义信息，我们默认点云的语义信息已经知道了。对于两帧点云P1P2，我们从中筛选出具有语义代表性的点，比如建筑物、交通标志等内容，其余的点则忽略不计。
对于其中的每个点，将它们向二维平面上投影，以激光雷达为中心，计算其极坐标和平面坐标：

之后依然是按照角度划分扇形区域，在传统的Scan Context编码中，在每个扇区内还要沿径向在继续划分格子，这里就不需要这一步了，每个扇区内，只保留径向上离圆心最近的点，如果一共划分N个扇区，那么经过这一步的处理，就可以用一个N维向量来表示。

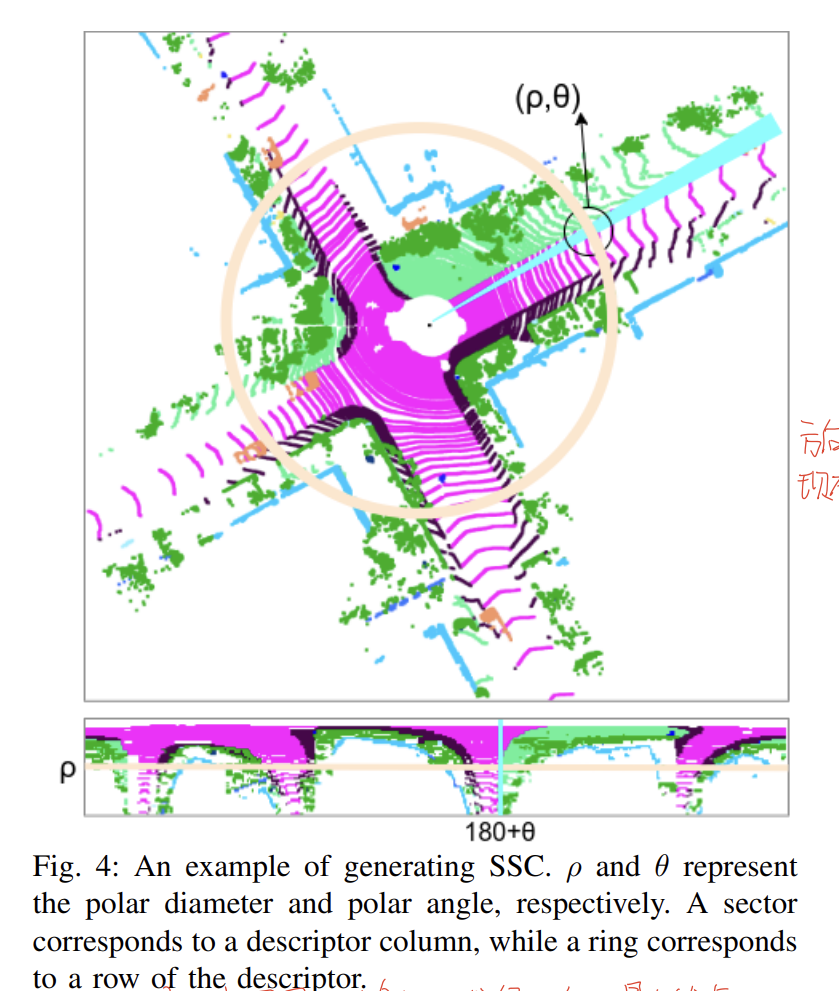
之后我们就利用这个N维向量来快速计算角度，这一步很像是图像匹配里面的全局旋转角计算，只不过这里使用的是最近点的径向距离。

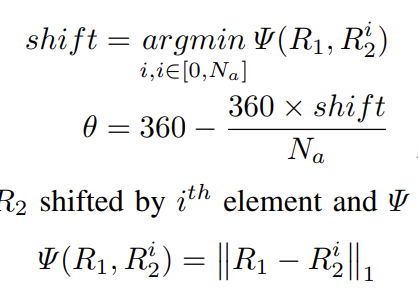
这篇论文通过这种类似于角度直方图的方法，将点云角度上进行了一个对齐操作，相当于给原始的Scan Context补上了一个旋转不变性，但是降维的方法有些太直接了，直接是取了每个径向上的最小值，也可能是个人理解错了，对于普通的道路来说，取最小值的方法难道不是直接扫描到地面上吗，那这样子到哪里都是扫到地面，角度对齐的意义不就没了。

快速语义ICP

经过上一步，我们得到了两帧点云之间的角度偏差，那么我们可以利用这个角度偏差，将点云旋转到同一个方向上：

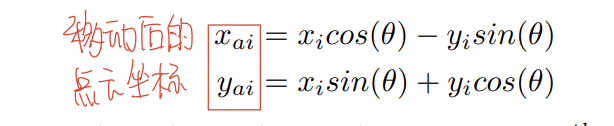
转换之后，点云的角度实际上是对齐了的，那么区别就只在于中心的位置了，由于使用的是投影之后的结果，所以差距就是Δx和Δy，可以利用下面的式子进行优化：

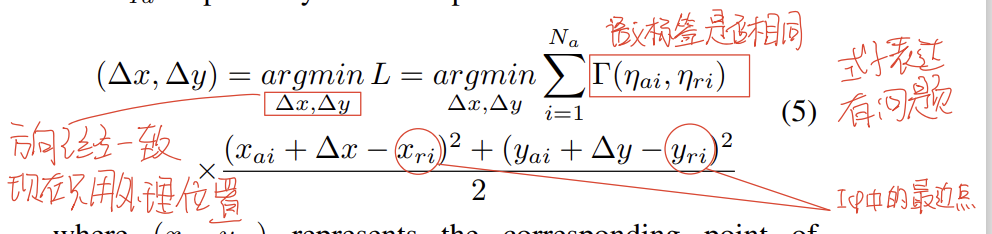
这个式子中，第二行就是一个ICP的变式，将ICP计算位姿换为了求Δx和Δy，关键在于第一行最后的这个函数是用来衡量两个标签是否相同的二值函数，如果相同返回值是1，如果不同，返回值是0。这个式子的意思都可以理解，就是考虑最近点语义相同的情况下，用ICP找一个最近距离从而优化出Δx和Δy，但这个式子的写法有问题，如果找到了一个Δx和Δy让所有点的语义标签都不一样，这个式子的结果是0，必然是目标函数的最小值，也就是说式子将一个完全错误的Δx和Δy认为是最优值，虽然可能性不是很大，但不排除有这种可能，个人感觉式子写法上应该加一个标签相同的点的数量的比例，用这个来衡量语义一致性的程度。

三、语义结合的Scan Context

上面的部分提供了一种快速的语义结合的相似度检测方法，除此之外，论文还对Scan Context进行了改进，将语义信息引入了进去，依然是使用原始的划分网格的方法，这次我们直接统计落入网格内标签的情况：

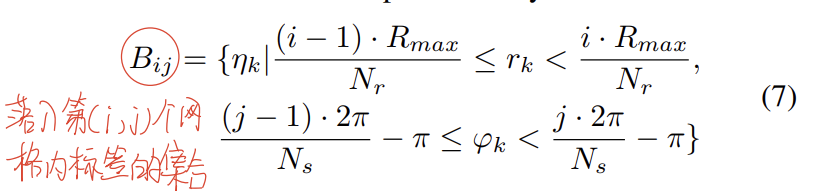
之后对于每个网格，根据语义标签的统计信息来进行编码：

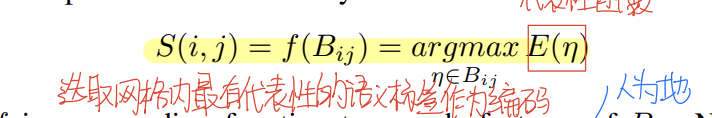
这里的E是一个函数，论文里面没有给出具体的写法，只提到这是一个用于衡量代表性的函数，标签出现的次数越少就认为其代表性越高，就选择这个标签作为这个网格的编码，由此可以得到一个基于语义的二维矩阵编码。
那么我们就可以在上面对齐之后的点云的基础上做进一步的编码，用这个方法得到一个语义、位置结合在一起的编码，并且由于点云已经对齐，所以不需要在匹配时额外考虑列寻找的事情，直接对对应位置做匹配就可以：

最后的相似度计算公式相当于是一个相同标签的网格占全体网格的比例，用这个值来衡量两帧点云的相似程度。