Polygon zkEVM Memory Align状态机

1. 引言

前序博客有：

• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机

Memory Align状态机为Polygon zkEVM的六个二级状态机之一，该状态机内包含：

• executor part：sm_mem_align.js：负责生成execution trace，为常量多项式和隐私多项式赋值。
• 验证规则集PIL：mem_align.pil：定义了约束系统。

Polygon zkEVM Memory状态机通过使用a 32-byte word access来检查内存读写，而EVM支持对单个byte级别的offset进行读写。

如下图，分别表示了相同内容在 byte级别 和 32-byte级别的内存布局：

A D D R E S S B Y T E 0 0 x c 4 1 0 x 17 ⋮ ⋮ 30 0 x 81 31 0 x a 7 32 0 x 88 33 0 x d 1 ⋮ ⋮ 62 0 x b 7 63 0 x 23

ADDRESS01⋮30313233⋮6263​BYTE0xc40x17⋮0x810xa70x880xd1⋮0xb70x23​​

ADDRESS 32-BYTE   WORD 0 0 x c 417...81 a 7 1 0 x 88 d 1... b 723

ADDRESS01​32-BYTE WORD0xc417...81a70x88d1...b723​​

32-byte与byte级别布局之间的关系称为“memory alignment”，而Memory Align状态机负责检查二者之间关系的正确性。

EVM支持3种内存操作：

• 1）MLOAD：按指定offset地址读取内存，返回内存中自该offset开始的32字节word。【注意，MLOAD可读取2个不同words的bytes。】【对应zkasm中的MEM_ALIGN_WR】
• 2）MSTORE：按指定offset地址存储32byte。【对应zkasm中的MEM_ALIGN_RD】
• 3）MSTOREE：将某单个byte数据存入指定offset地址。【注意，MSTOREE为按单个byte写入。】【对应zkasm中的MEM_ALIGN_WR8】

EVM是按byte级别操作的，仍以上表为例，对应2个word：
$${\mathtt{m}}_0=0x88d11f\cdots b723,{\mathtt{m}}_1=0x6e21ff\cdots 54f9.$$
当MLOAD 0x22时，返回的结果为：
$$\mathtt{val}=0x1f\cdots b7236e21.$$
跨越了2个word，将该读操作的结果标记为：${\mathtt{m}}_0\mid {\mathtt{m}}_1$：

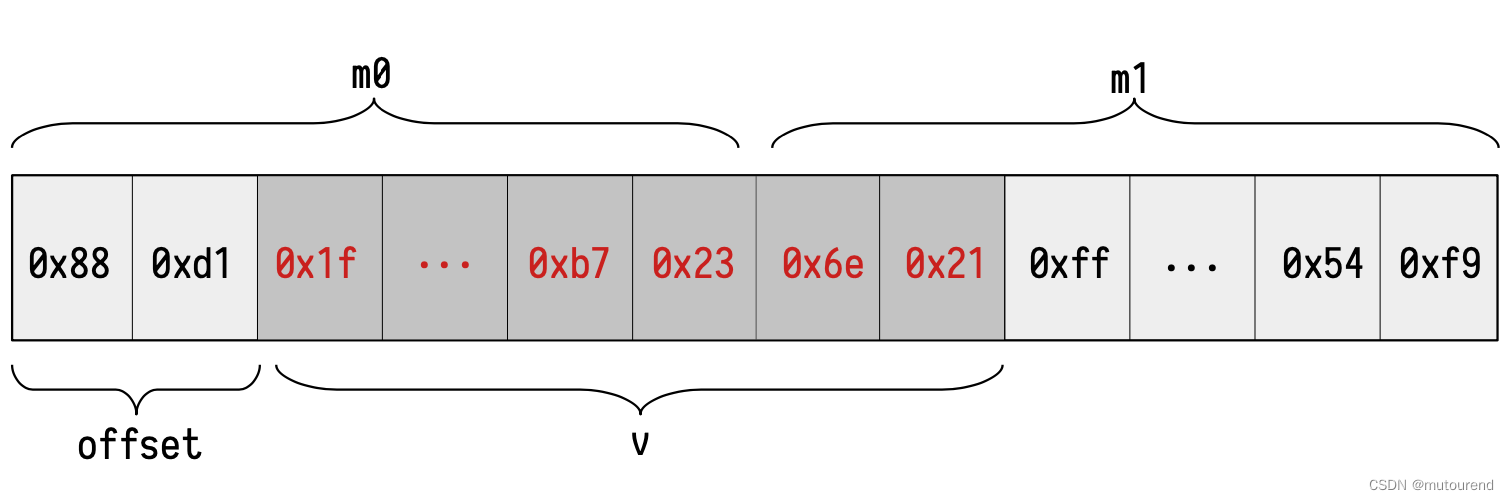
验证MLOAD 0x22返回的结果$0x1f\cdots 7236e21$是否正确的流程为：

• 1）Main状态机需查询获得${\mathtt{m}}_0$ 和 ${\mathtt{m}}_1$值；
• 2）Main状态机需调用Memory状态机来验证所查询的结果有效；
• 3）Main状态机可很容易extract the memory positions to query from the address 0x22。事实上，若$a$为MLOAD操作的内存位置，则${\mathtt{m}}_0$总是存储在内存位置$\lfloor \frac{a}{32}\rfloor$ 且 ${\mathtt{m}}_1$ 存储在内存位置$\lfloor \frac{a}{32}\rfloor +1$。本例中 $a=0x22=34$，从而 ${\mathtt{m}}_0$ 存储在位置$\lfloor \frac{32}{34}\rfloor =0x01$ 且 ${\mathtt{m}}_1$ 存储在位置 $\lfloor \frac{32}{34}\rfloor +1=0x02$。
• 4）应从正确的offset提取，offset应为0-31的index，表示从${\mathtt{m}}_0$的读取$\mathtt{val}$的偏移位置。如本例中，offset为2（即offset为 $a\mathrm{mod}32$）。可借助Plookup来验证已知${\mathtt{m}}_0,{\mathtt{m}}_1$和$\mathtt{offset}$，所读取的$\mathtt{val}$值是正确的。

同理，对于$\mathtt{MSTORE}$为write bytes in two words。假设${\mathtt{w}}_0,{\mathtt{w}}_1$为${\mathtt{m}}_0,{\mathtt{m}}_1$进行$\mathtt{MSTORE}$操作之后的值。
如MSTORE 0x22 0xe201e6...662b，想要向基于单个字节布局的以太坊内存中的0x22地址写入：
$$\mathtt{val}=0xe201e6\dots 662b$$
写入成功之后，相应的${\mathtt{w}}_0,{\mathtt{w}}_1$值为：
$${\mathtt{w}}_0=0x88d1e201e6\dots ,{\mathtt{w}}_1=0x662b\mathtt{ff}\dots 54f9$$

已知：

• 1）an address $\mathtt{addr}$
• 2）an offset value $\mathtt{offset}$
• 3）待写入的值 $\mathtt{val}$

Main状态机的操作与上面MLOAD类似，只是改为需要检查${\mathtt{w}}_0,{\mathtt{w}}_1$确实是根据已知的$\mathtt{val},{\mathtt{m}}_0,{\mathtt{m}}_1,\mathtt{offset}$构建的。

2. Memory Align状态机的约束系统

mem_align.pil中的常量多项式赋值情况见：Polygon zkEVM中的常量多项式中“mem_align.pil中的常量多项式”。

mem_align.pil中的隐私多项式有：

    * OPERATIONS
    *
    *  (m0,m1,D) => v
    *  (m0,m1,D,v) => (w0, w1)
    *
    *  @m0 = addr   @m1 = addr + 32 (ethereum)
    *
    *  Ethereum => BigEndian
    *  m0[7],m0[6],...,m0[1],m0[0],m1[7],m1[6],...,m1[1],m1[0]
    *
    *  inM (8 bits, 32 steps)
    */

    // 32 bytes of M0, M1 ordered from HSB to LSB (32, 31, 30, ... == M[7].3, M[7].2, M[7].1, M[7].0, M[6].3, ..)
    pol commit inM[2];

    // 32 bytes of V
    pol commit inV;

    // write 32 bytes (256 bits)
    pol commit wr256;

    // write 1 byte (8 bits), its special case because need to ignore
    // the rest of bytes, only LSB of V was stored (on w0 with offset)
    pol commit wr8;

    pol commit m0[8];
    pol commit m1[8];
    pol commit w0[8];
    pol commit w1[8];
    pol commit v[8];

    // when m1 is "active", means aligned with inV
    // also when wr8 = 1, used to indicate when store the LSB
    pol commit selM1;

    // factors to build V[] in correct way, because order of V bytes
    // changes according the offset and wr8
    pol commit factorV[8];

    pol commit offset;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

基本的约束为：

	//              RangeCheck                  Latch   Clock
    // factorV      Plookup (FACTORV)           no      yes
    // wr256        Plookup (WR256)             yes     no
    // wr8          Plookup (WR8)               yes     no
    // offset       Plookup (OFFSET)            yes     no
    // inV          RangeCheck (BYTE_C3072)     no      yes
    // inM[0..1]    RangeCheck (BYTE2A,BYTE2B)  no      yes
    // m0[0..7]     Built                       no      yes
    // m1[0..7]     Built                       no      yes
    // w0[0..7]     Built                       no      yes
    // w1[0..7]     Built                       no      yes
    // v[0..7]      Built                       no      yes
    // selM1        Plookup (SELM1)             no      yes
1
2
3
4
5
6
7
8
9
10
11
12
13

• 1）借助RESET常量多项式，对wr256、offset、wr8隐私多项式进行锁存约束：

  // Latchs
  (1 - RESET) * wr256' = (1 - RESET) * wr256;
  (1 - RESET) * offset' = (1 - RESET) * offset;
  (1 - RESET) * wr8' = (1 - RESET) * wr8;
  1
  2
  3
  4

• 2）约束inM[1]的取值范围为 BYTE2A 【= 0 (x256), 1 (x256), 2 (x256), …, 255 (x256)】，约束inM[0]的取值范围为 BYTE2B 【= 0, 1, 2, 4, **, 255, 0, 1, …, 255】：

  // RangeCheck
  {inM[1], inM[0]} in {BYTE2A, BYTE2B};
  1
  2

• 3）约束offset、wr256、wr8、selM1、inv、factorV[0-7]的取值：

  // Plookup
  {
      STEP, offset', wr256', wr8', selM1, inV,
      factorV[0], factorV[1], factorV[2], factorV[3], factorV[4], factorV[5], factorV[6], factorV[7]
  } in {
      STEP, OFFSET, WR256, WR8, SELM1, BYTE_C3072,
      FACTORV[0], FACTORV[1], FACTORV[2], FACTORV[3], FACTORV[4], FACTORV[5], FACTORV[6], FACTORV[7]
  };
  1
  2
  3
  4
  5
  6
  7
  8

• 4）约束m0[0-7]与m1[0-7]的transition约束为：

  m0[0]' = (1-RESET) * m0[0] + FACTOR[0] * inM[0];
  m0[1]' = (1-RESET) * m0[1] + FACTOR[1] * inM[0];
  m0[2]' = (1-RESET) * m0[2] + FACTOR[2] * inM[0];
  m0[3]' = (1-RESET) * m0[3] + FACTOR[3] * inM[0];
  m0[4]' = (1-RESET) * m0[4] + FACTOR[4] * inM[0];
  m0[5]' = (1-RESET) * m0[5] + FACTOR[5] * inM[0];
  m0[6]' = (1-RESET) * m0[6] + FACTOR[6] * inM[0];
  m0[7]' = (1-RESET) * m0[7] + FACTOR[7] * inM[0];
  
  m1[0]' = (1-RESET) * m1[0] + FACTOR[0] * inM[1];
  m1[1]' = (1-RESET) * m1[1] + FACTOR[1] * inM[1];
  m1[2]' = (1-RESET) * m1[2] + FACTOR[2] * inM[1];
  m1[3]' = (1-RESET) * m1[3] + FACTOR[3] * inM[1];
  m1[4]' = (1-RESET) * m1[4] + FACTOR[4] * inM[1];
  m1[5]' = (1-RESET) * m1[5] + FACTOR[5] * inM[1];
  m1[6]' = (1-RESET) * m1[6] + FACTOR[6] * inM[1];
  m1[7]' = (1-RESET) * m1[7] + FACTOR[7] * inM[1];
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17

• 5）约束selM1与wr256、wr8之间的关系：

  // selW0 contains data to be store in w0, must be 0 in "reading mode"
  // in "writting mode", in particular with wr8 only on byte must be
  // stored, for this reason use selM1 that was active only one clock (in wr8 mode)
  pol selW0 = (1 - selM1) * wr256' + selM1 * wr8';
  
  // selW1 contains data to be store in w1, must be 0 in "reading mode"
  pol selW1 = selM1 * wr256';
  1
  2
  3
  4
  5
  6
  7

• 6）w0[0-7]和w1[0-7]的transition约束为：

  // NOTE: when wr8 = 1 implies wr256 = 0, check in this situations where use selM1
  // to verify that non exists collateral effects
  //
  // pol selW0 = selM1 (because wr256 = 0 and wr8 = 1)
  //
  // selM1 used in pol _inM, but _inM is only used on dataV
  // pol dataV = (1 - wr256' - wr8') * _inM + (wr256' + wr8') * inV;
  // pol dataV = inV (because wr256 = 0 and wr8 = 1)
  //
  // CONCLUSION: it's safe reuse selM1 to indicate when store byte
  
  // data to "write" on w, if current byte must be override by V contains inV
  // if not contains inM "in reading mode" must be 0.
  pol dataW0 = (wr8' + wr256') * inM[0] + selW0 * (inV - inM[0]);
  pol dataW1 = (wr8' + wr256') * inM[1] + selW1 * (inV - inM[1]);
  
  w0[0]' = (1-RESET) * w0[0] + FACTOR[0] * dataW0;
  w0[1]' = (1-RESET) * w0[1] + FACTOR[1] * dataW0;
  w0[2]' = (1-RESET) * w0[2] + FACTOR[2] * dataW0;
  w0[3]' = (1-RESET) * w0[3] + FACTOR[3] * dataW0;
  w0[4]' = (1-RESET) * w0[4] + FACTOR[4] * dataW0;
  w0[5]' = (1-RESET) * w0[5] + FACTOR[5] * dataW0;
  w0[6]' = (1-RESET) * w0[6] + FACTOR[6] * dataW0;
  w0[7]' = (1-RESET) * w0[7] + FACTOR[7] * dataW0;
  
  w1[0]' = (1-RESET) * w1[0] + FACTOR[0] * dataW1;
  w1[1]' = (1-RESET) * w1[1] + FACTOR[1] * dataW1;
  w1[2]' = (1-RESET) * w1[2] + FACTOR[2] * dataW1;
  w1[3]' = (1-RESET) * w1[3] + FACTOR[3] * dataW1;
  w1[4]' = (1-RESET) * w1[4] + FACTOR[4] * dataW1;
  w1[5]' = (1-RESET) * w1[5] + FACTOR[5] * dataW1;
  w1[6]' = (1-RESET) * w1[6] + FACTOR[6] * dataW1;
  w1[7]' = (1-RESET) * w1[7] + FACTOR[7] * dataW1;
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24
  25
  26
  27
  28
  29
  30
  31
  32
  33

• 7）v的transition约束：

  // _inM contains "active" value of inM
  pol _inM = (1 - selM1) * inM[0] + selM1 * inM[1];
  
  // contains data to store in V, could be one of inM if was reading or inV if was writting
  pol dataV = (1 - wr256' - wr8') * _inM + (wr256' + wr8') * inV;
  
  // factorV = f(STEP, offset, wr8)
  v[0]' = (1-RESET) * v[0] + factorV[0] * dataV;
  v[1]' = (1-RESET) * v[1] + factorV[1] * dataV;
  v[2]' = (1-RESET) * v[2] + factorV[2] * dataV;
  v[3]' = (1-RESET) * v[3] + factorV[3] * dataV;
  v[4]' = (1-RESET) * v[4] + factorV[4] * dataV;
  v[5]' = (1-RESET) * v[5] + factorV[5] * dataV;
  v[6]' = (1-RESET) * v[6] + factorV[6] * dataV;
  v[7]' = (1-RESET) * v[7] + factorV[7] * dataV;
  1
  2
  3
  4
  5
  6
  7
  8
  9
  10
  11
  12
  13
  14
  15

3. Memory Align状态机示例

可参见zkevm-proverjs/test/sm/sm_mem_align_test.js或zkevm-proverjs/test/counters/mem_align.js，输入为test/zkasm/counters/mem_align.zkasm。
Memory Align状态机对应的zkasm基本语法为：【其中的值为BigEndian表示】

# 1. 按C偏移读取32-byte
0x0102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E2021n => A
0xA0A1A2A3A4A5A6A7A8A9AAABACADAEAFB0B1B2B3B4B5B6B7B8B9BABBBCBDBEBFn => B
5 => C
$ => A :MEM_ALIGN_RD
0x060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E2021A0A1A2A3A4n :ASSERT

# 2. 按C偏移写入32-byte
0x0102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E2021n => A
0xA0A1A2A3A4A5A6A7A8A9AAABACADAEAFB0B1B2B3B4B5B6B7B8B9BABBBCBDBEBFn => B
31 => C
0x0102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E20C0n => D
0xC1C2C3C4C5C6C7C8C9CACBCCCDCECFD0D1D2D3D4D5D6D7D8D9DADBDCDDDEDFBFn => E
0xC0C1C2C3C4C5C6C7C8C9CACBCCCDCECFD0D1D2D3D4D5D6D7D8D9DADBDCDDDEDFn :MEM_ALIGN_WR

# 3. 按C偏移写入一个byte。BigEndian表示，最低byte在最右侧。
0x0102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E2021n => A
1 => C       
0x01DF030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E2021n => D      
0xC0C1C2C3C4C5C6C7C8C9CACBCCCDCECFD0D1D2D3D4D5D6D7D8D9DADBDCDDDEDFn :MEM_ALIGN_WR8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

参考资料

[1] Memory Align SM

附录：Polygon Hermez 2.0 zkEVM系列博客

• ZK-Rollups工作原理
• Polygon zkEVM——Hermez 2.0简介
• Polygon zkEVM网络节点
• Polygon zkEVM 基本概念
• Polygon zkEVM Prover
• Polygon zkEVM工具——PIL和CIRCOM
• Polygon zkEVM节点代码解析
• Polygon zkEVM的pil-stark Fibonacci状态机初体验
• Polygon zkEVM的pil-stark Fibonacci状态机代码解析
• Polygon zkEVM PIL编译器——pilcom 代码解析
• Polygon zkEVM Arithmetic状态机
• Polygon zkEVM中的常量多项式
• Polygon zkEVM Binary状态机
• Polygon zkEVM Memory状态机