一文搞懂mysql索引底层逻辑，干货满满！

一、什么是索引

在mysql中,索引是一种特殊的数据库结构,由数据表中的一列或多列组合而成,可以用来快速查询数据表中有某一特定值的记录。通过索引,查询数据时不用读完记录的所有信息,而只是查询索引列即可，索引是帮助Mysql高效获取数据且以排好序的数据结构，直观的说，索引就类似书的目录页，没有目录（即索引）我们就要一页一页的找，有了目录（索引）我们就可以按照目录中标记的页数去相应的页数去查找。

二、为什么要用索引

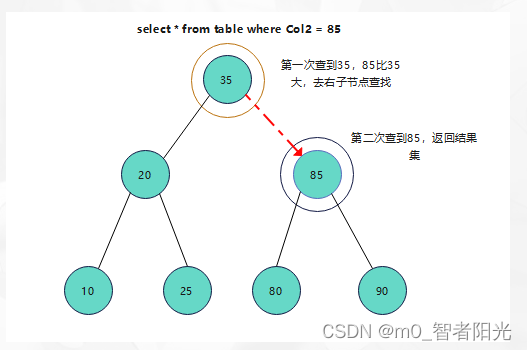
 例如，我们通过查询语句查询一条记录：select * from table where Col2 = 85,如果没有索引的话，那么它将从第一行[1,35]开始找，一行一行的找，直到找到[6,85]这条数据，并且数据存放的位置也不规则，拿取一行记录就需要与磁盘进行一次交互，即IO读取，如果数据多，这种效率将会很低下，只要把这种交互次数控制在一定范围之内，那他的效率将会比一行行查找要高很多，如给col2加索引，来执行select * from table where Col2 = 85，通过二叉树接口，第一次我们查到的是35，85比35大，所以查找右子节点，查到85，与条件种的85为一条数据，所以，这里就只需要两次交互就可以查到。所以索引就诞生了。

 

 

三、索引的数据结构

1、二叉树

1.1、二叉树的特点：

　　1、每个节点最多有两个子树，所以二叉树不存在度大于2的节点（结点的度：结点拥有的 子树的数目。），可以没有子树或者一个子树。
　　2.左子树和右子树有顺序，次序不能任意颠倒。
　　3、二叉树支持动态的插⼊和查找，保证操作在O(height)时间，这就是完成了哈希表不便完成的⼯作，动态性。但是⼆叉树有可能出现worst-case，如果　　　　　　　　　　　　 输⼊序列已经排序，则时间复杂度为O(N)。为什么不用二叉树来作为索引，就是因为二叉树的worst-case，如果输入序列是排好序的，那么二叉树的结构就会变成如下图所示的特殊状态：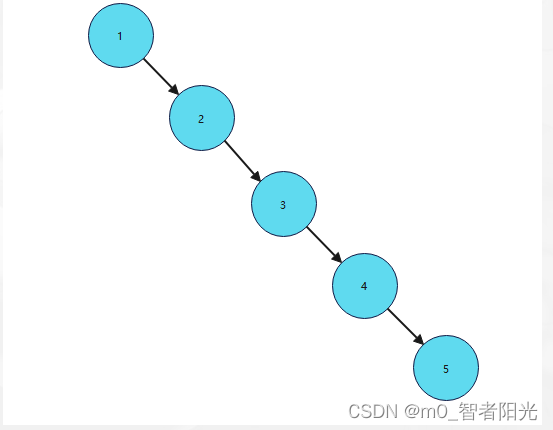

 

 

所以二叉书并不适合去做索引，遇到这种极端情况，就会导致有索引和无索引效果一样。

2、平衡二叉树

AVL树是严格的平衡二叉树，所有节点的左右子树高度差不能超过1；AVL树查找、插入和删除在平均和最坏情况下都是O(lgn)。AVL实现平衡的关键在于旋转操作：插入和删除可能破坏二叉树的平衡，此时需要通过一次或多次树旋转来重新平衡这个树。当插入数据时，最多只需要1次旋转(单旋转或双旋转)；但是当删除数据时，会导致树失衡，AVL需要维护从被删除节点到根节点这条路径上所有节点的平衡，旋转的量级为O(lgn)。由于旋转的耗时，AVL树在删除数据时效率很低；在删除操作较多时，维护平衡所需的代价可能高于其带来的好处，因此AVL实际使用并不广泛。

3、红黑树

与AVL树相比，红黑树并不追求严格的平衡，而是大致的平衡：只是确保从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。从实现来看，红黑树最大的特点是每个节点都属于两种颜色(红色或黑色)之一，且节点颜色的划分需要满足特定的规则。在java8中的HashMap就是使用链表+红黑树。红黑树的缺点就是太高了，如下图所示：

 

当数据量特别大的时候，树的高度很高，假设你要查找的节点为当前树的叶子节点，那么要查找这个节点，至少要循环h(这棵树的高度)次，所以说，红黑树在这种情况下也并不适用。

4、B-Tree

Tree就是我们常说的B树，它是一种多路搜索树而非二叉树，使用B-tree结构可以显著减少定位记录时所经历的中间过程，从而加快存取速度

在B树中，每个节点包含：

1、本结点所含关键字的个数；

2、指向