算法提高： 使用归并实现范围和问题（Count of Range Sum）

问题描述

给定一个整数数组，返回range sum 落在给定区间[lower, upper] (包含lower和upper)的个数。range sum S(i, j) 表示数组中第i 个元素到j 个元素之和。

Note:
A naive algorithm of O(n2) is trivial. You MUST do better than that.

Example:

Input: nums = [-2,5,-1], lower = -2, upper = 2,
Output: 3
Explanation: The three ranges are : [0,0], [2,2], [0,2] and their respective sums are: -2, -1, 2.

思路

这个题目可以使用有序表做，也可以使用分治的思想去做，不论如何，O(n2) 的时间复杂度都可以想办法优化到O（Nlogn）.

这里主要讲分治的思想。

有一个前置知识点是前缀和，前缀和（Prefix Sum）的定义为：对于一个给定的数列 A, 它的前缀和数列 S 是通过递推能求出来得

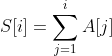
部分和。

所以：

1. 设置双指针，分别为left_window,right_window；

        因为是排序后的数组，所以左右均有序；

2. 根据right_window,求出递增的range pair list；

3. 在left_windows 中设置双指针 分别为L、R；

    3.1 L 指向第一个大于range的pair的左值，R指向第一个小于range pair的右值，求出Count +=(R-L +1 )；

   3.2 L向前找到大于第二个range的pair的左值，R指向第二个小于range pair的右值，求出Count +=(R-L +1 )；

   3.3. 直到L >=R;

4. 正常merge

因为，merge这个环节，都是不回头的遍历，所以时间复杂度为O(N)

归并本身的时间复杂度为O（LogN）,所以最终的时间复杂度为（O（NlogN）)）

代码

typedef long long ll;
 
class Solution {
public:
    int countRangeSum(vector<int>& nums, int lower, int upper) {
        int n = nums.size();
        if (n == 0) return 0;
        vector sum(n+1, 0);
        for (int i = 0; i < n; i++) {
            sum[i+1] = sum[i] + nums[i];
        }
        return countRangeSum(sum, lower, upper, 0, n + 1);
    }
    int countRangeSum(vector& sum, int lower, int upper, int left, int right) {
        if (left + 1 >= right) return 0;
        int res = 0;
        int mid = (right + left) >> 1;
        res += countRangeSum(sum, lower, upper, left, mid) + countRangeSum(sum, lower, upper, mid, right);
        for (int i = left; i < mid; i++) {
            res += distance(lower_bound(sum.begin() + mid, sum.begin() + right, sum[i] + lower), 
                    upper_bound(sum.begin() + mid, sum.begin() + right, sum[i] + upper));
        }
        inplace_merge(sum.begin()+left, sum.begin()+mid, sum.begin()+right);
        // merge(sum.begin() + left, sum.begin() + mid, sum.begin() + mid, sum.begin() + right, sum.begin() + left);
        return res;
    }
};