因果系列文章（7）——干预工具（下）

在上一节我们继续学习了有关干预的知识，具体来说，学习了三种重要的干预工具：后门调整、前门调整、逆概率加权。在本节中，我们从线性系统开始入手，介绍变量连续时的因果效应如何表达，并学习中介、工具变量等概念。

本章将结束因果分析中干预的讲解，在理论与工具之外我会引入系统——关河因果分析系统来举例说明干预的过程，便于大家理解。

路径系数&回归系数

之前介绍的模型中变量都是二值的，现实中的很多事件变量都是连续的。比如我们想知道课外辅导和考试成绩的关系、上网学慕课和未来找工作的关系等等。那么一种最简单的建模方法就是用线性系统建模。具体来说，变量之间的关系都是线性的。而之前使用概率来表示变量之间依赖关系的形式就要相应的变成期望的形式了。

比如之前表示，以 Z 为条件， Y 和 X 是相互独立的，我们写作

P(Y|X,Z)=P(Y|Z)

而对于连续变量，我们就写作

E[Y|X,Z]=E[Y|Z]

条件期望也就可以写成线性的形式

E[Y|X1=x1,X2=x2,…,Xn=xn]=r0+r1x1+r2x2+···+rnxn

其中 r1,r2,…,rn 被称为回归系数（或者相关系数）。这些回归系数 ri 的值与 xi 的值无关，只与谁是回归因子有关。换句话说， 无论Xi=1 、 Xi=2 还是 Xi=312.3 ，只要我们选择了 Xi 作为回归因子，那么回归系数就是不变的。

回归系数是表示变量之间的统计特征，也就是我们站在因果关系之梯第一层级用观测数据归纳出的，它只是对客观事实的描述， y=r1x+r2z+ 不能说明 X 和 Z 是 Y 的因。与回归系数不同，路径系数则反映的是变量之间的因果关系或者结构关系，是因果关系之梯第二层级的信息。比如我们定义 Y=3X+U 这就说明 X 和 Y 之间有因果关系路径X→Y ，且路径系数为3。每一个路径系数都表示一条因果关系。在《Causal Inference in Statistics》一书中，路径系数用 α,β 来表示，而回归系数用 r1,r2 等等来表示。

考虑下图中的图模型。其中 a,b,c,d,e 分别标出了五条因果关系路径的路径系数。

 

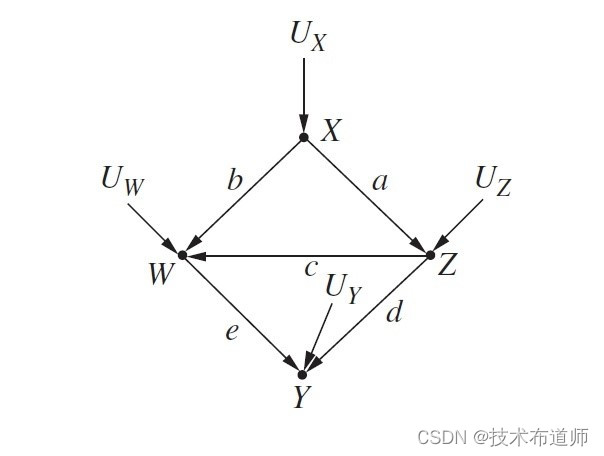
图1

假设我们想要计算 Z 对 Y 的因果效应的总和。那么计算的方式就是将每一条因果路径上的因果系数与对应变量相乘，然后对所有非后门路径求和。

Y=dZ+eW+UY

=dZ+e(bX+cZ)+UY+eUW

=(d+ec)Z+ebX+UY+eUW 

这表明对 Z 每增加一个单位， Y 将随之增加 d+ec 个单位。比较一下， d+ec 、 eb 其实就是回归系数，是 Z 对 Y 、X 对 Y 的总效应。而 d 和