【LeetCode】二叉树题总结（持续更新）

理论

《代码随想录》

144. 二叉树的前序遍历（递归与迭代）

144. 二叉树的前序遍历

中左右：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int>ans;
        traversal(root,ans);
        return ans;
    }

    void traversal(TreeNode *root,vector<int>&ans){
        if(root==NULL) return;
        ans.push_back(root->val);
        traversal(root->left,ans);
        traversal(root->right,ans);
        
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

栈：中右左。
动图见这里

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int>ans;
        if(!root) return ans;
        stack<TreeNode*>st;
        st.push(root);
        while(st.size()){
            TreeNode* node=st.top();
            st.pop();
            ans.push_back(node->val);
            if(node->right) st.push(node->right);
            if(node->left) st.push(node->left);
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

94. 二叉树的中序遍历（递归与迭代）

94. 二叉树的中序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>ans;
        traversal(root,ans);
        return ans;
    }
    void traversal(TreeNode *root,vector<int>&ans){
        if(root==NULL) return;
        traversal(root->left,ans);
        ans.push_back(root->val);
        traversal(root->right,ans);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int>ans;
        stack<TreeNode*>st;
        if(!root) return ans;
        TreeNode* now=root;
        while(now||st.size()){
            if(now){
                st.push(now);          //左
                now=now->left;
            }else{
                ans.push_back(st.top()->val);     //中          
                now=st.top()->right;        //右
                st.pop();
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

145. 二叉树的后序遍历（递归与迭代）

145. 二叉树的后序遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int>ans;
        traversal(root,ans);
        return ans;
    }
    void traversal(TreeNode *root,vector<int>&ans){
        if(root==NULL) return;
        traversal(root->left,ans);
        traversal(root->right,ans);
        ans.push_back(root->val);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int>ans;
        stack<TreeNode*>st;
       
        if(!root) return ans;
        st.push(root);
        while(st.size()){
            TreeNode* temp=st.top();
            ans.push_back(temp->val);
            st.pop();
            if(temp->left) st.push(temp->left);
            if(temp->right) st.push(temp->right);
        }
        reverse(ans.begin(),ans.end());
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

102. 二叉树的层序遍历

102. 二叉树的层序遍历

类似BFS的模板了。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>>ans;
        if(!root) return ans;
        queue<TreeNode*>q;
        q.push(root);
        while(q.size()){
            vector<int>temp;
            int s=q.size();
            for(int i=0;i<s;i++){
                TreeNode* now=q.front();
                q.pop();
                temp.push_back(now->val);
                if(now->left) q.push(now->left);
                if(now->right) q.push(now->right);
            }
            ans.push_back(temp);
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

226. 翻转二叉树

226. 翻转二叉树

感觉层序遍历最直观。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*>q;
        if(!root) return NULL;

        TreeNode* now;
        q.push(root);
        while(q.size()){
            int s=q.size();
            for(int i=0;i<s;i++){
                now=q.front();
                q.pop();

                swap(now->left,now->right);
                if(now->left) q.push(now->left);
                if(now->right) q.push(now->right);
            }           
        }
        return root;
    }
    
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

101. 对称二叉树

101. 对称二叉树

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        TreeNode* le;
        TreeNode* ri;
        
        queue<TreeNode*>q;
        q.push(root->left);
        q.push(root->right);

        while(q.size()){
            le=q.front();q.pop();
            ri=q.front();q.pop();

            //都空
            if(!le&&!ri) continue;
            //都不空且相等
            else if(le&&ri&&le->val==ri->val){
                q.push(le->left);
                q.push(ri->right);
                q.push(le->right);
                q.push(ri->left);
            }
            else return false;
        }
        return true;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

222. 完全二叉树的节点个数（利用完全二叉树性质）

222. 完全二叉树的节点个数

class Solution {
public:
    int countNodes(TreeNode* root) {
        if(!root) return 0;
        TreeNode* le=root->left,*ri=root->right;

        int leNum=0,riNum=0;
        while(le){
            leNum++;
            le=le->left;
        }
        while(ri){
            riNum++;
            ri=ri->right;
        }

        //满二叉树  
        if(leNum==riNum){
            return (2<<leNum)-1;
        }

        return countNodes(root->left)+countNodes(root->right)+1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

110. 平衡二叉树（递归）

110. 平衡二叉树

class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(getHeight(root)!=-1) return true;
        else return false;
    }

    //二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。
    int getHeight(TreeNode *root){
        if(!root) return 0;
        
        int le=getHeight(root->left);
        int ri=getHeight(root->right);
        if(le==-1||ri==-1) return -1;
        else return abs(le-ri)>1?-1:max(le,ri)+1;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

100. 相同的树（递归）

100. 相同的树

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        return check(p,q);
    }

    bool check(TreeNode* t1,TreeNode* t2){
        if(!t1&&!t2) return true;
        else if(t1&&!t2) return false;
        else if(!t1&&t2) return false;
        else if(t1&&t2&&t1->val!=t2->val) return false;

        bool ans=check(t1->left,t2->left)*check(t1->right,t2->right);
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

257. 二叉树的所有路径（经典dfs）

257. 二叉树的所有路径

class Solution {
public:
    vector<string>res;
    vector<string> binaryTreePaths(TreeNode* root) {
        res.clear();
        if(!root) return res;
        vector<int>ans;
        ans.push_back(root->val);
        dfs(root,ans);
        return res;
    }

    void dfs(TreeNode* node,vector<int>&ans){
        //到底了
        if(!node->left&&!node->right){
            res.push_back(IntToString(ans));
        }
        else{
            if(node->left){
            ans.push_back(node->left->val);
            dfs(node->left,ans);
            ans.pop_back();
            }
            if(node->right){
                ans.push_back(node->right->val);
                dfs(node->right,ans);
                ans.pop_back();
            }
        }      
    }

    string IntToString(vector<int>ans){
        string anss;
        for(int i=0;i<ans.size();i++){
            anss+=to_string(ans[i]);
            if(i!=ans.size()-1) anss+="->";
        }
        return anss;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

113. 路径总和 II（经典dfs）

113. 路径总和 II

做这道题的时候有一种在打天梯赛的感觉。

class Solution {
public:
    vector<vector<int>>ans;
    int targetSum1;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(!root) return ans;
        targetSum1=targetSum;
        vector<int>anss;
        anss.push_back(root->val);
        dfs(root,anss,root->val);
        return ans;
    }

    void dfs(TreeNode* now,vector<int>&anss,int sum){
        //叶子节点
        if(!now->left&&!now->right){
            if(sum==targetSum1){
                ans.push_back(anss);
            }
        }else{
            if(now->left){
                sum+=now->left->val;
                anss.push_back(now->left->val);
                dfs(now->left,anss,sum);
                sum-=now->left->val;
                anss.pop_back();
            }
            if(now->right){
                sum+=now->right->val;
                anss.push_back(now->right->val);
                dfs(now->right,anss,sum);
                sum-=now->right->val;
                anss.pop_back();
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

106. 从中序与后序遍历序列构造二叉树（递归构造二叉树）

106. 从中序与后序遍历序列构造二叉树

有一种在做天梯赛的感觉。
这里是左闭右开。

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if(postorder.size()==0) return NULL;
        return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());
    }

    //中l，中r，后l，后r
    //左闭右开
    TreeNode* traversal(vector<int>& inorder,int zl,int zr,vector<int>&postorder,int hl,int hr){
        if(hl==hr) return NULL;

        //根
        int val=postorder[hr-1];
        TreeNode* root=new TreeNode(val);

        //分割
        int zhong;
        for(int i=zl;i<zr;i++){
            if(inorder[i]==val){
                zhong=i;
                break;
            }
        }

        //左子树 zl,zhong
        root->left= traversal(inorder,zl,zhong,postorder,hl,hl+zhong-zl);

        //右子树 zhong+1,zr
        root->right= traversal(inorder,zhong+1,zr,postorder,hr+zhong-zr,hr-1);

        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

105. 从前序与中序遍历序列构造二叉树（递归构造二叉树）

105. 从前序与中序遍历序列构造二叉树

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0) return NULL;
        return traversal(preorder,0,preorder.size(),inorder,0,inorder.size());
    }

    //q前，z中
    TreeNode* traversal(vector<int>& preorder,int ql,int qr,vector<int>& inorder,int zl,int zr){
        if(ql==qr) return NULL;

        //根
        int val=preorder[ql];
        TreeNode* root=new TreeNode(val);

        //分割
        int zhong;
        for(int i=zl;i<zr;i++){
            if(inorder[i]==val){
                zhong=i;
                break;
            }
        }

        //左 zl,zhong
        root->left=traversal(preorder,ql+1,zhong-zl+ql+1,inorder,zl,zhong);

        //右
        root->right=traversal(preorder,qr+zhong+1-zr,qr,inorder,zhong+1,zr);

        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

654. 最大二叉树（递归+构造）

654. 最大二叉树

与上面的递归很像。
也是左闭右开。

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if(nums.size()==0) return NULL;
        return solve(nums,0,nums.size());
    }

    TreeNode* solve(vector<int>&nums,int l,int r){
        if(l>=r) return NULL;

        //根
        int val=-1,index;
        for(int i=l;i<r;i++){
            if(nums[i]>val){
                val=nums[i];
                index=i;
            }           
        }

        TreeNode* root=new TreeNode(val);

        //左
        root->left=solve(nums,l,index);
        //右
        root->right=solve(nums,index+1,r);

        return root;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

98. 验证二叉搜索树（有坑：中序遍历+二叉搜索树的性质）

98. 验证二叉搜索树

这题有坑。不能简单地比较一个节点的左右子节点的大小，因为二叉搜索树要求整个左子树都要小，整个右子树都要大。

如：这里，6确实小于15，但它在10的右子树上。如果只是比较一个节点的左右节点，就会错。

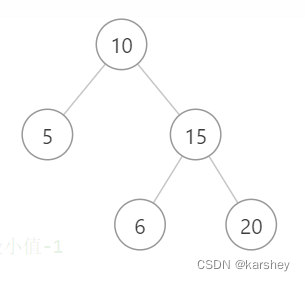
正确思路：中序遍历（左中右），若是递增的就是二叉搜索树。

注意看数据范围。

class Solution {
public:
    bool isValidBST(TreeNode* root) {

        //加了这一句快了好多
        ans.clear();
        solve(root);

        //注意数据范围：这里要初始化成最小值-1
        long long last=-2147483649;
        for(long long u:ans){
            if(u<=last) return false;
            last=u;
        }

        return true;
    }

    vector<long long>ans;
    void solve(TreeNode* root){
        if(!root) return;
        solve(root->left);
        ans.push_back(root->val);
        solve(root->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26