【LeetCode-112】路径总和

8.4 路径总和

8.4.1 题目描述

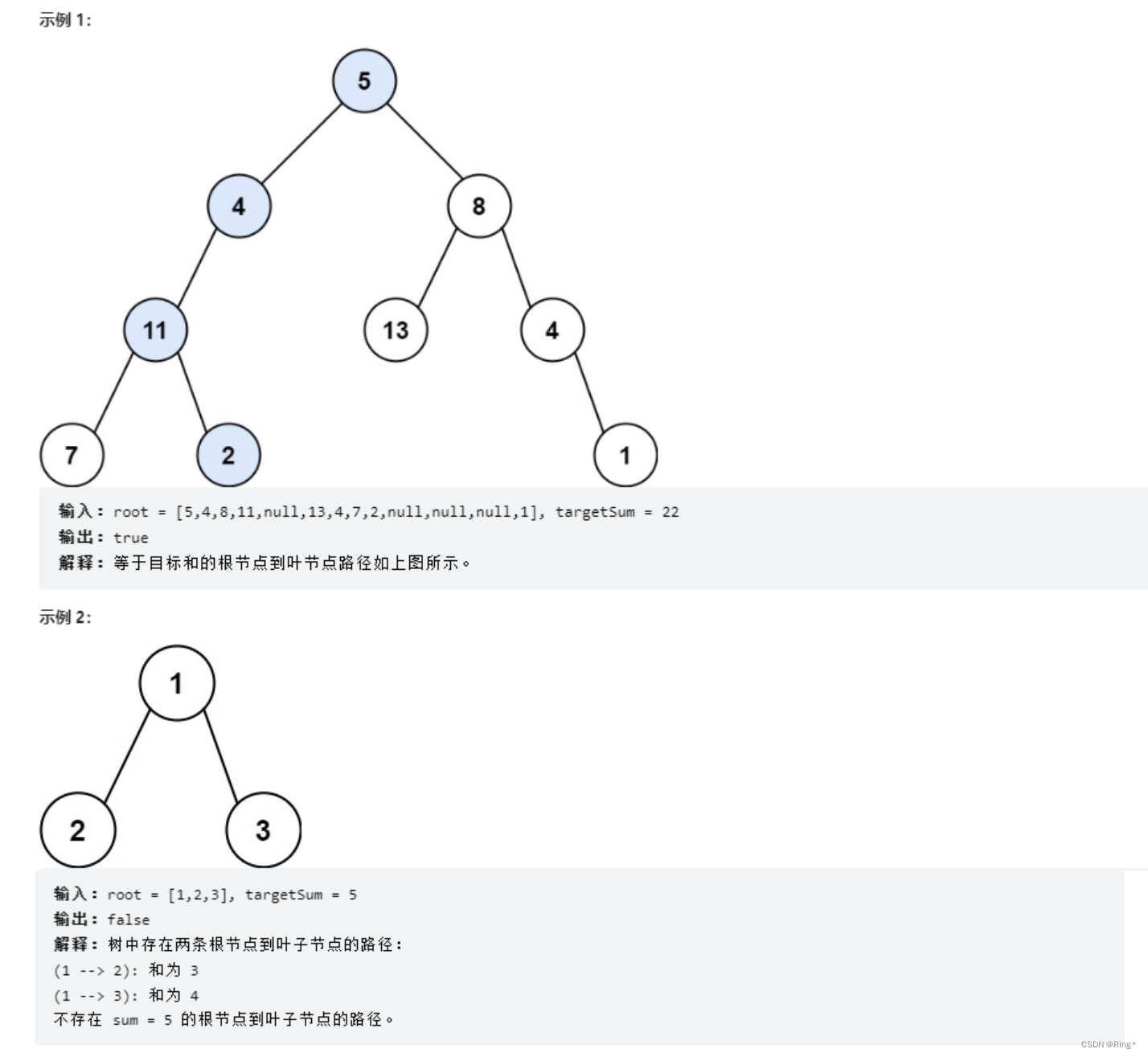
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

写在前面
注意到本题的要求是，询问是否有从「根节点」到某个「叶子节点」经过的路径上的节点之和等于目标和。核心思想是对树进行一次遍历，在遍历时记录从根节点到当前节点的路径和，以防止重复计算。

需要特别注意的是，给定的 root 可能为空。

8.4.2 方法一：广度优先搜索

思路及算法

首先我们可以想到使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。

这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        Queue<TreeNode> queNode = new LinkedList<TreeNode>();
        Queue<Integer> queVal = new LinkedList<Integer>();
        queNode.offer(root);
        queVal.offer(root.val);
        while (!queNode.isEmpty()) {
            TreeNode now = queNode.poll();
            int temp = queVal.poll();
            if (now.left == null && now.right == null) {
                if (temp == sum) {
                    return true;
                }
                continue;
            }
            if (now.left != null) {
                queNode.offer(now.left);
                queVal.offer(now.left.val + temp);
            }
            if (now.right != null) {
                queNode.offer(now.right);
                queVal.offer(now.right.val + temp);
            }
        }
        return false;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

复杂度分析

• 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
• 空间复杂度：O(N)，其中 N 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

思路及算法

观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。

代码

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}
1
2
3
4
5
6
7
8
9
10
11

复杂度分析

• 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
• 空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(logN)。

8.4.3 方法二：递归

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}
1
2
3
4
5
6
7
8
9
10
11

8.4.4 my answer—递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null)return false;
        if(root.left == null && root.right == null){
            return root.val == targetSum;
        }
        return hasPathSum(root.left,targetSum - root.val) || hasPathSum(root.right,targetSum - root.val);

    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25