【牛客刷题】带你在牛客刷题第八弹（简单排序）

目录

第一题 Laptop

题目描述

输入描述:

输出描述:

示例1

备注:

讲解

AC 

 第二题 [NOIP2010]导弹拦截

题目描述

输入描述:

输出描述:

示例1

示例2

备注:

讲解

AC

 哈喽，今天是我们牛客刷题训练第八弹，今天我们来刷一些简单排序的问题，这些问题相对于之前的C/C++基础来说难度肯定是高出了一些，但是我相信，只要我们一步步去分析，最后肯定是可以得到正确的答案的，来我们一起加油。

第一题 Laptop

题目描述

FST是一名可怜的小朋友，他很强，但是经常fst，所以rating一直低迷。
但是重点在于，他非常适合ACM！并在最近的区域赛中获得了不错的成绩。
拿到奖金后FST决定买一台新笔记本，但是FST发现，在价格能承受的范围内，笔记本的内存和速度是不可兼得的。
可是，有一些笔记本是被另外一些“完虐”的，也就是内存和速度都不高所以于另外某一个笔记本，现在FST想统计一下有多少笔记本被“完虐”。

输入描述:

第一行一个正整数n，
表示笔记本的数量。接下来n行，每行两个正整数Mi，Si表示这款笔记本的内存和速度。
n≤105,Mi,Si≤109

输出描述:

一行，一个正整数，表示被完虐的笔记本数。

示例1

输入

4
100 700
200 500
50 100
300 400

输出

1

备注:

Mi和Si都是越大越优。
数据保证Mi互不相同，Si也互不相同。

讲解

这道题目就是我们要去判断两个数都不大于其他数的数，这里我们可以将两个数据放入pair里面，然后对他进行排序（调用函数），然后我们先对前面一个数排序，然后前面数相等就对后面数排序，之后我们要进行遍历这些元素，这些元素的前面数都是已经排序过的，这时我们一直维护第二个数的最大值然后对数据进行比较就可以了。

AC 

#include
#include
#include
 
using namespace std;
 
pair<int, int> a[100010];
 
int main()
{
    int n, j, k;
    cin >> n;
    for (int i = 0;i < n;i++)
    {
        scanf("%d%d",&j,&k);
        a[i].first = j;
        a[i].second = k;
    }
    sort(a, a + n);
    int ans = 0;
    j = n - 1;
    for (int i = n - 2;i >= 0;i--)
    {
 
        if (a[j].second > a[i].second)
        {
            if (a[j].first > a[i].first)
                ans++;
        }
        else j = i;
    }
    cout << ans << endl;
    return 0;
}

 第二题 [NOIP2010]导弹拦截

题目描述

经过11年的韬光养晦，某国研发出了一种新的导弹拦截系统，凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为0时，则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷：每套系统每天只能设定一次工作半径。而当天的使用代价，就是所有系统工作半径的平方和。

某天，雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段，所以只有两套系统投入工作。如果现在的要求是拦截所有的导弹，请计算这一天的最小使用代价。

输入描述:

第一行包含4个整数x_1、y_1、x_2、y_2x1​、y1​、x2​、y2​，每两个整数之间用一个空格隔开，表示这两套导弹拦截系统的坐标分别为(x_1, y_1)、(x_2, y_2)(x1​,y1​)、(x2​,y2​)。
第二行包含1个整数N，表示有N颗导弹。接下来N行，每行两个整数x、y，中间用一个空格隔开，表示一颗导弹的坐标(x, y)。不同导弹的坐标可能相同。

输出描述:

输出只有一行，包含一个整数，即当天的最小使用代价。

示例1

输入

0 0 10 0
2
-3 3
10 0

输出

18

说明

要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为18和0。

示例2

输入

0 0 6 0 
5 
-4 -2 
-2 3 
4 0 
6 -2 
9 1

输出

30

说明

样例中的导弹拦截系统和导弹所在的位置如下图所示。要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为20和10。

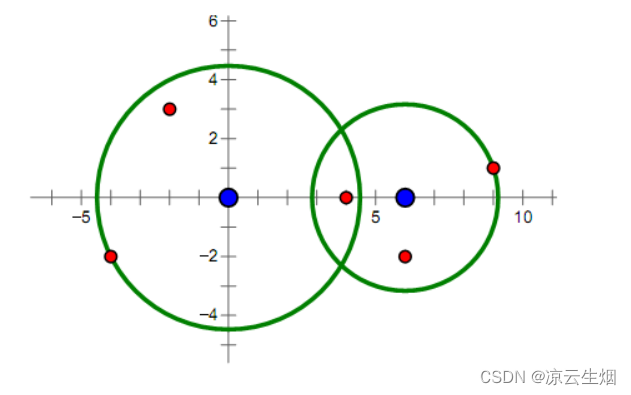
备注:

两个点(x_1, y_1)、(x_2, y_2)(x1​,y1​)、(x2​,y2​)之间距离的平方是(x_1−x_2)^2+(y_1−y_2)^2(x1​−x2​)2+(y1​−y2​)2。
两套系统工作半径r_1、r_2r1​、r2​的平方和，是指r_1、r_2r1​、r2​分别取平方后再求和，即r_1^2+r_2^2r12​+r22​。
对于10%的数据，N=1N=1
对于20%的数据，1≤N≤21≤N≤2
对于40%的数据，1≤N≤1001≤N≤100
对于70%的数据，1≤N≤10001≤N≤1000
对于100%的数据，1≤N≤1000001≤N≤100000，且所有坐标分量的绝对值都不超过1000。

讲解

这个题目我们可以先将每个导弹与第一个系统的距离的平方算出来，然后再对距离的平方进行从大到小排序，从1开始枚举每个导弹由二系统拦截的情况，每次更新二系统的最大半径和答案的最小值，这样我们就可以求出使用的最小代价了。

AC

#include
#include
#include
 
using namespace std;
 
int x1,yl,x2,y2,n,ans,r1,r2;
 
struct node{
 
    int x,y,d1;
 
}mis[100005]; //表示横纵坐标和与一系统的距离平方
 
int dis(int x,int y,int a,int b)
 
{
 
    return (x-a)*(x-a)+(y-b)*(y-b);
 
} //因为精度的问题所以直接用平方来存距离
 
bool cmp(node a,node b)
 
{
 
    return a.d1>b.d1;
 
} //由大到小排序
 
int main()
 
{
 
    int x,y;
 
    scanf("%d%d%d%d%d",&x1,&yl,&x2,&y2,&n);
 
    for(int i=1;i<=n;i++)
 
    {
 
        scanf("%d%d",&x,&y);
 
        mis[i].x=x;
 
        mis[i].y=y;
 
        mis[i].d1=dis(x1,yl,mis[i].x,mis[i].y);
 
    }
 
 
 
    sort(mis+1,mis+n+1,cmp);
 
 
 
    r1=mis[1].d1;
 
    ans=r1;
 
    for(int i=2;i<=n+1;i++) //一定要注意这里是n+1，因为可能一系统一个导弹都没拦截
 
    {
 
        r1=mis[i].d1;
 
        r2=max(r2,dis(x2,y2,mis[i-1].x,mis[i-1].y)); //更新二系统半径平方最大值
 
        ans=min(ans,r1+r2); //更新答案最小值
 
    }
 
    printf("%d",ans);
 
    return 0;
 
}