-
【通信】Matlab实现改进的多同步压缩变换
1 内容介绍
多重同步压缩变换简介
在分析一个客观物体时,采集它当前状态的信息,是了解其工作状况最好的方式。通过传感器,记录其信息,得到的就是信号(一般均为时域信号)。时频分析技术(TFA),通过加入频率变量,为我们分析时域信号,提供了更为全面的时频视角。但是,传统TFA是存在很多不足的。这里不再赘述。
相关文章谷歌搜索“Multi-synchrosqueezing Transform”即可。
目前,TFA的发展,是冲着两个目标。
一,时频谱具有高能量聚集性,直观地可以理解为高时频分辨率(也有些人,反对将聚集性等同为分辨率)。
二,信号能够被完美重构。(做到完美重构的话,可以使得该TFA技术用于信号去噪,模态分解等方面。)
传统TFA方法,比如,短时傅里叶变换(STFT),小波变换(WT),S变换等等,都是可以做到信号被完美重构的。但是,它们的能量聚集性特别差,时频谱发散严重。同步压缩变换(SST)的出现,就是在不影响信号重构性能的前提下,提高能量聚集性。但是,SST对噪声敏感,并且不适合处理强调频信号(遇到这两种情况,依然会发散严重)。上面的帖子中,介绍了一种叫同步提取变换(SET)的方法。相比于SST,时频聚集性,得到极大的提高。但是,SET不再能够完美重构信号了,只能做到近似重构。
这就有点尴尬了,难道上面两个目标,就不能同时达成吗?!接下来,介绍一种新提出的算法,Multi-synchrosqueezing Transform(MSST),多重同步压缩变换。MSST,既可以实现高能量聚集性,也可以完美重构信号。MSST是基于SST的一种技术,但是,脑洞却开的相当大。了解SST的同仁们应该知道,SST是基于STFT(或者WT)的一种后处理工具,从频率方向对STFT的结果进行压缩,从而提升时频谱的能量聚集性。此刻,大家心里还需要清楚一件事,只要是在频率方向对STFT结果进行的压缩,永远都可以对时域信号进行完美重构。虽然,SST不太适合处理强调频信号。但是,对强调频信号的STFT结果进行SST处理之后,时频谱依然要更加聚集一些。重点来了!那么,我们是不是可以对SST结果继续执行一次同步压缩操作?答案当然是可以的。再执行一次SST操作的结果是,时频谱会更加聚集。那么,继续执行下去,时频谱是不是会继续聚集下去?yes!通过这些idea的汇集,就提出了MSST算法。其原理,就是对时频谱执行多次同步压缩操作。由于多次压缩都是在频率方向进行的,因此,MSST是允许信号被完美重构的。
当然了,执行多次同步压缩,是会产生巨大的计算负担的,不利于实时计算。因此,之后文章中又给出了一种通过函数迭代的方式,极大地减少了计算负担,可以做到与SST相同的计算复杂度,实时性很好。
MSST从构思上,从算法实现上,都非常的简单。但是,其深层的数学原理,却很深。接下来,给大家看一个蝙蝠信号的分析例子。其他的,可以从文章中看看。文章最后,也提供了所有的代码和数据。直接拖进MATLAB里就可以运行。
2 部分代码
clear;
close all
load('batdata2.mat');
SampFreq = 1000000/7;
n=length(data);
time=(1:n)/SampFreq;
fre=(SampFreq/2)/(n/2):(SampFreq/2)/(n/2):(SampFreq/2);
time=time*1000;
fre=fre/1000;
[Ts] = IMSST_Z(data,45,10);
%[Ts] = IMSST_Z(data);
figure;
imagesc(time,fre,abs(Ts));
xlabel('Time (s)');
ylabel('Fre (Hz)');
axis xy
3 运行结果
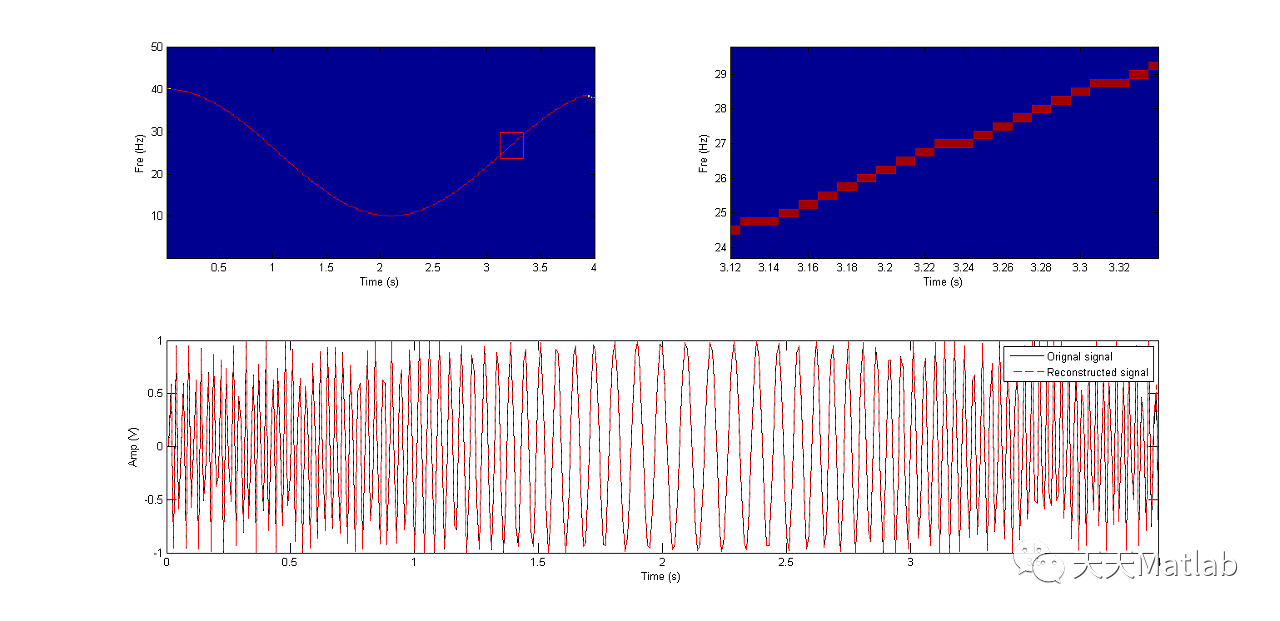

4 参考文献
[1]曹宏瑞, 周铖, 魏江,等. 一种基于改进同步压缩变换的扭振信号瞬时频率提取方法:.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机、雷达通信、无线传感器等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。
-
相关阅读:
[python数据处理系列] 深入理解与实践:用Python进行主成分分析(PCA)
前端性能精进之浏览器(五)——JavaScript
jsp源码商城系统Myeclipse开发mysql数据库servlet开发java编程计算机网页项目
Java多线程核心工具类
【第16章】Vue实战篇之跨域解决
实现页面全局Loading进度条实现
Linux学习记录——삼 基本指令(3)及了解权限
el-popover放在el-table中点击无反应问题
使用JMeter进行接口测试教程
教你用Perl实现Smgp协议
- 原文地址:https://blog.csdn.net/qq_59747472/article/details/126735089