数据结构之八大排序——简单选择排序

---

目录

一、排序过程

二、代码

三、性能及稳定性分析

1.空间复杂度

2.时间复杂度

3.稳定性

---

一、排序过程

假设待排序的序列为L[1...n]，第i趟排序是从L[i...n]中从i开始遍历选择一个关键字最小的元素与L(i)交换位置，每一趟排序可以确定一个元素的最终位置，经过n-1趟排序可使得排序表有序。

二、代码

public class SelectionSort {
    public static void main(String[] args) {
        int[] arr = {1, 7, 4, 9, 6, 7, 2, 5};
        System.out.print("排序前为：");
        for (int i : arr) {
            System.out.print(i + " ");
        }
        System.out.println();
        selection(arr);
        System.out.print("排序后为：");
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }
 
    public static void selection(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {      //进行排序的趟数n-1趟
            int min = i;                                //假定每一趟第i个元素为最小元素
            for (int j = min + 1; j < arr.length; j++) {    //在arr[i...n-1]中选择最小的元素
                if (arr[j] < arr[min]) {            //判断元素是否小于arr[min]
                    min = j;                        //如果在arr[i...n-1]中有比arr[min]小的元素就将其下标赋给min
                }
            }
            if (min != i) {                         //判断最小元素是否为第i个并对交换arr[i]arr[min]
                int temp = arr[min];
                arr[min] = arr[i];
                arr[i] = temp;
            }
        }
    }
}

选择排序的过程：

 

结果： 

 

三、性能及稳定性分析

1.空间复杂度

因为排序的整个过程中，仅在当前的数组中操作，没有使用另一个空数组，仅使用了常熟个辅助单元，因此时间复杂度为O(1)

2.时间复杂度

最好情况为起始序列有序，移动0次。但是元素之间的比较次数与序列的起始状态无关，始终是n(n-1)/2次。

所以时间复杂度始终是。

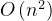3.稳定性

由上图对简单选择排序的分析，红色的7开始在白色的7前面，在进行第二趟排序的时候红色的7被交换到后面。因此简单选择排序是一个不稳定的排序。

---

​