【计算机视觉】OpenCV算法解析

0. 前言

此篇主要介绍opencv大坑，以及对前面没有学到的比较简单的常见算法进行补充：包括最小二乘法、RANSAC、哈希算法

1. OpenCV

• OpenCV是一个开源的计算机视觉库。OpenCV 库用C语言和 C++ 语言编写，可以在 Windows、Linux、Mac OS X 等系统运行。同时也在积极开发Python、Java、Matlab 以及其他一些语言的接口，将库导入安卓和 iOS 中为移动设备开发应用。

• opencv大坑之BGR

  opencv对于读进来的图片的通道排列是BGR，而不是主流的RGB

  #opencv读入的矩阵是BGR，如果想转为RGB，可以这么转 
  img4 = cv2.imread('1.jpg') 
  img4 = cv2.cvtColor(img4,cv2.COLOR_BGR2RGB) 
  1
  2
  3

• 使用OpenCV优势

  1. 除了opencv读入的彩色图片以BGR顺序存储外，其他所有图像库读入彩色图片都以RGB存储。

  2. 除了PIL读入的图片是img类之外，其他库读进来的图片都是以numpy 矩阵。

  3. 各大图像库的性能，最好的OpenCV，无论是速度还是图片操作的全面性，都属于碾压的存在，毕竟他是一个巨大的cv专用库。

• OpenCV常见算法

  1. 图像的基本操作读取、显示、存储：通过调用OpenCV中的cv2.imread()，cv2.imshow()，cv2.write()分别实现。

  2. 在OpenCV中实现将彩色像素转化为灰度像素。

  3. 图像的几何变换：平移、缩放、旋转、插值（最近邻、双线性）。

  4. 对比增强：线性变换、伽马变换、直方图均衡化。

  5. 边缘检测：Sobel、Canny

  6. 图像的二维滤波：cvFilter2D

2. 线性回归算法：最小二乘法

复习：线性回归

举个例子，某商品的利润在售价为2元、5元、10元时分别为4元、10元、20元，我们很容易得出商品的利润与售价的关系符合直线：y=2x.在上面这个简单的一元线性回归方程中，我们称“2”为回归系数，即斜率为其回归系数。回归系数表示商品的售价(x)每变动一个单位，其利润(y)与之对应的变动关系。

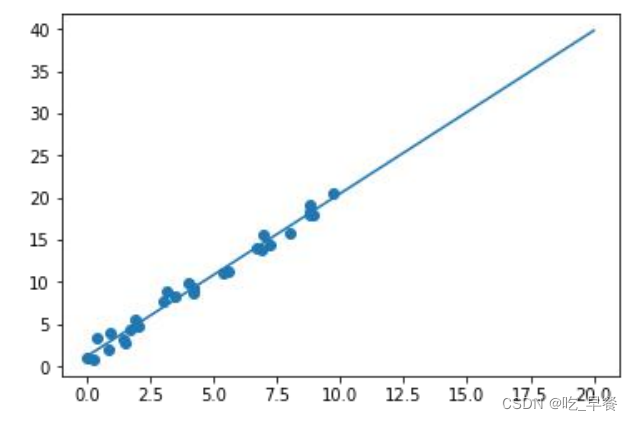
线性回归表示这些离散的点总体上“最逼近”哪条直线。

• 最小二乘法：通过最小化误差的平方和，寻找数据的最佳函数匹配。 （也就是寻找最佳的那条直线，最终就是寻找残差的最小值）最小二乘法通过计算最小均方差关于参数a、b的偏导数为零时的值。事实上，很多情况下，最小二乘法都是线性回归的代名词。

• 利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

• 解释：假设我们现在有一系列的数据点(xi,yi) (i=1,…,m)，那么由我们给出的拟合函数h(x)得到的估计量就是h(xi) 。残差：ri = h(xi) – y

• 适用情况：最小二乘法只适合于误差较小的情况，因为该算法不会去除噪声(离群数据)，故会对最后的结果产生影响。

• 三种范数： (计算残差)

  • ∞-范数：残差绝对值的最大值，即所有数据点中残差距离的最大值：

    （数据多时计算量太大，不具有可操作性）
    $$ma{x}_{1\le i\le m}|r_i|$$

  • 1-范数：绝对残差和，即所有数据点残差距离之和：

    （数据多时计算量太大，不具有可操作性）
    $$\sum _{i=1}^m|r_i|$$

  • 2-范数：残差平方和：（ 一般都选择二范式）
    $$\sum _{i=1}^m{r_i}^2$$

• 拟合程度：我们的拟合函数h(x)与待求解的函数y之间的相似性。

  2-范数越小，相似性就比较高。

• 算法最终目的：找一个残差的最小值，然后找到最佳函数（对应于以下公式中的平方和最小的时候的k和b的值）
  $$mi{n}_{a,b}\sum _{n=1}^N(y_n-(k\times x+b){)}^2$$

  这是一个无约束的最优化问题，根据以上公式分别对k和b求偏导，然后令偏导数为0，即可获得极值点。
  k = N ∑ n = 1 N