【牛客 - 剑指offer】JZ43 整数中1出现的次数（从1到n整数中1出现的次数）两种方案 Java实现

---

剑指offer题解汇总 Java实现

https://blog.csdn.net/guliguliguliguli/article/details/126089434

本题链接

知识分类篇 - 其他算法 - JZ43 整数中1出现的次数（从1到n整数中1出现的次数）

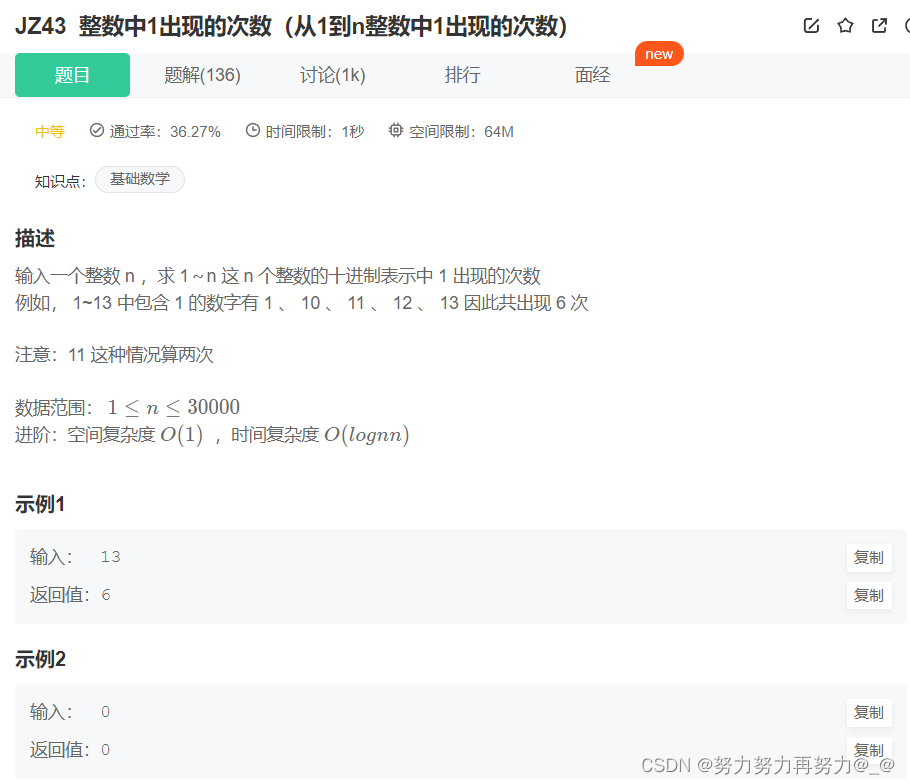
题目

思路 & 代码

方案一（暴力）

遍历从1到n的每一个数，首先判断这个数的范围，然后计算每一位上的数字是不是1

import java.util.*;

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {

        if (n == 0) {
            return 0;
        }

        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            cnt += cal(i);
        }
        return cnt;

    }

    private int cal(int i) {
        if (i < 10) {
            return (i % 10 == 1 ? 1 : 0);
        } else if (i < 100) {
            return (i % 10 == 1 ? 1 : 0) + ((i / 10) % 10 == 1 ? 1 : 0);
        } else if (i < 1000) {
            return (i % 10 == 1 ? 1 : 0) + ((i / 10) % 10 == 1 ? 1 : 0) + ((i / 100) % 10 == 1 ? 1 : 0);
        } else if (i < 10000) {
            return (i % 10 == 1 ? 1 : 0) + ((i / 10) % 10 == 1 ? 1 : 0) + ((i / 100) % 10 == 1 ? 1 : 0) + ((i / 1000) % 10 == 1 ? 1 : 0);
        }else {
            return (i % 10 == 1 ? 1 : 0) + ((i / 10) % 10 == 1 ? 1 : 0) + ((i / 100) % 10 == 1 ? 1 : 0) + ((i / 1000) % 10 == 1 ? 1 : 0) + ((i / 10000) % 10 == 1 ? 1 : 0);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import java.util.*;

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {

        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            for (int j = i; j > 0; j /= 10) {
                if (j % 10 == 1) {
                    cnt++;
                }
            }
        }
        return cnt;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

方案二 按位计算（推荐，数学方法）

这里的按位计算，就比如，传入的n是12235

1. 计算1到12235的所有数字中个位是1的出现次数
2. 计算1到12235的所有数字中十位是1的出现次数
3. 计算1到12235的所有数字中百位是1的出现次数
4. 计算1到12235的所有数字中千位是1的出现次数
5. 计算1到12235的所有数字中万位是1的出现次数
6. 最后把1、2、3、4、5的结果加一起，就是1到12235这些数字中1出现次数的总数

import java.util.*;

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n) {
        int res = 0;
        //MulBase = 10^i
        long MulBase = 1;
        //每位数按照公式计算
        while (MulBase <= n){
            //根据公式添加
            res += (n / (MulBase * 10)) * MulBase + Math.min(Math.max(n % (MulBase * 10) - MulBase + 1, (long) 0), MulBase);
            //扩大一位数
            MulBase *= 10;
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

以12235为例，答案是：7990
计算个位上1出现的次数：

• 0到9之间，个位上有一个1，10到19之间，个位上有1个1，可以看出，每增加10，就会有1个1
  • 在12235这个例子中
    • 12235/10=1223，也就是说，从10到1235之间，个位上有1223个1
    • 然后对12235取余，12235%10=5，在数字0到数字9之间，还会出现一个1
    • 所以，在1到12235之间，所有数字，个位上出现的1的个数是1223+1=1224

计算十位上1出现的次数：

• 如果传入的数字小于10，那么不存在对十位上的计算
• 10到19，十位上有10个1，100到119，十位上又是10个1，可以看出，每增加100，就会有10个1
  • 在12235这个例子中
    • 12235/100=122，也就是说，从100到12235之间，十位上有122x10=1220个1
    • 12235%100=35，在10到35之间，十位上有10个1
    • 所以，在1到12235之间，所有数字，十位上出现1的个数是1220+10=1230

计算百位上1出现的次数：

• 如果传入的数字小于100，那么不存在对百位上的计算
• 100到199，百位上有100个1，1100到1199，百位上又是100个1，可以看出，每增加1000，就会有100个1
  • 在12235这个例子中
    • 12235/1000=12，也就是说，从1000到12235之间，百位上有12x100=1200个1
    • 12235%1000=235，在100到235之间，百位上有100个1
    • 所以，在1到12235之间，所有数字，百位上出现1的个数是1200+100=1300

计算千位上1出现的次数：

• 如果传入的数字小于1000，那么不存在对千位上的计算
• 1000到1999，千位上有1000个1，11000到11999，千位上又是1000个1，可以看出，每增加10000，就会有1000个1
  • 在12235这个例子中
    • 12235/10000=1，也就是说，从10000到12235之间，千位上有1x1000=1000个1
    • 12235%10000=2235，在1000到2235之间，千位上有1000个1
    • 所以，在1到12235之间，所有数字，千位上出现1的个数是1000+1000=2000

计算万位上1出现的次数

• 如果传入的数字小于10000，那么不存在对万位上的计算
• 10000到19999，万位上有10000个1
  • 在12235这个例子中
    • 12235/100000=0
    • 12235%100000=12235
    • 所以，10000到12235之间，万位上有12235-10000+1=2236个1

将所有结果加起来
1224+1230+1300+2000+2236=7990，与代码运行结果一样