【Leetcode刷题Python】337. 打家劫舍 III

1 题目

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

示例 1:

输入: root = [3,2,3,null,3,null,1]
输出: 7
解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7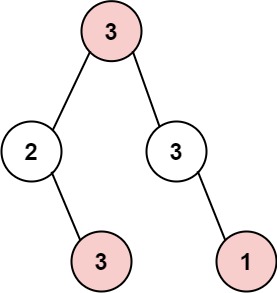

示例 2:

输入: root = [3,4,5,1,3,null,1]
输出: 9
解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

2 解析

用后续遍历的方法

$r_Y$：表示右孩子被选中
$r_N$：表示右孩子没有被选中
$l_N$：表示左孩子被选中
$l_N$：表示左孩子被选中

• 当 i 被选中时，i的左右孩子都不能被选中，故i被选中情况下子树上被选中点的最大权值和为 l和 r 不被选中的最大权值和相加，即
  $$f(i)=l_N+r_N$$

• 当 i不被选中时，i的左右孩子可以被选中，也可以不被选中。则权重为两种情况相加，即
  f ( i ) = m a x { l Y , l N } + m a x { r Y , r N } f(i)= max \{ l_Y,l_N\}+max\{ r_Y , r_N\} f(i)=max{lY​,lN​}+max{rY​,rN​}

3 python 实现

class Solution:
    def rob(self, root: Optional[TreeNode]) -> int:
        def rob_tree(root):
            if not root:return 0,0
            l_Y,l_N = rob_tree(root.left)
            r_Y,r_N = rob_tree(root.right)
            return root.val+l_N+r_N,max(l_Y,l_N)+max(r_Y,r_N)
        return max(rob_tree(root)) 
1
2
3
4
5
6
7
8