LeetCode307 周赛（补记）

2383.赢得比赛需要得最少训练时长

题目描述

你正在参加一场比赛，给你两个 正 整数 initialEnergy 和 initialExperience 分别表示你的初始精力和初始经验。

另给你两个下标从 0 开始的整数数组 energy 和 experience，长度均为 n 。

你将会 依次 对上 n 个对手。第 i 个对手的精力和经验分别用 energy[i] 和 experience[i] 表示。当你对上对手时，需要在经验和精力上都 严格 超过对手才能击败他们，然后在可能的情况下继续对上下一个对手。

击败第 i 个对手会使你的经验 增加 experience[i]，但会将你的精力 减少 energy[i] 。

在开始比赛前，你可以训练几个小时。每训练一个小时，你可以选择将增加经验增加 1 或者 将精力增加 1 。

返回击败全部 n 个对手需要训练的 最少 小时数目。

思路

按照题意，简单模拟即可。遍历一次，每次遇到一个对手，看当前的精力和经验是否足够击败他，若是，直接操作并更新精力和经验值；若否，则补足相差的部分，并进行累加记录。

class Solution {
    public int minNumberOfHours(int initialEnergy, int initialExperience, int[] energy, int[] experience) {
        int ans = 0;
        int n = energy.length;
        int curEn = initialEnergy, curEx = initialExperience;
        for (int i = 0; i < n; i++) {
            if (curEn <= energy[i]) {
                ans += energy[i] - curEn + 1;
                curEn = energy[i] + 1;
            }
            if (curEx <= experience[i]) {
                ans += experience[i] - curEx + 1;
                curEx = experience[i] + 1;
            }
            curEn -= energy[i];
            curEx += experience[i];
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

2384.最大回文数字

题目描述

给你一个仅由数字（0 - 9）组成的字符串 num 。

请你找出能够使用 num 中数字形成的 最大回文 整数，并以字符串形式返回。该整数不含 前导零 。

注意：

你 无需 使用 num 中的所有数字，但你必须使用 至少 一个数字。
数字可以重新排序。

思路

要构造一个回文串，并且要构造最大回文串。那么回文串的长度应该尽可能的长，回文串中的数字，靠近左边的要尽可能的大。那么我们对字符串num遍历一次，统计每个数字的出现次数，然后进行构造即可。

从9到0枚举数字，能保证构造出来的回文数字最大。

依次看每个数字的出现次数，第一次遇到奇数次数的，取这个数作为中间位置的数（能构造奇数长度的回文串就尽量构造奇数长度的），然后对于次数大于等于2的数，取偶数个该数字即可。

class Solution {
    public String largestPalindromic(String num) {
        int[] cnt = new int[10];
        for (int i = 0; i < num.length(); i++) cnt[num.charAt(i) - '0']++;
        int mid = -1; //长度为奇数时, 中间的数
        List<int[]> list = new ArrayList<>(); // 数字和次数
        for (int i = 9; i >= 0; i--) {
            if (cnt[i] == 0) continue;
            if ((cnt[i] & 1) == 1 && mid == -1) mid = i; // 第一次遇到次数为奇数的数字
            if (cnt[i] > 1) {
                int n = (cnt[i] & 1) == 1 ? cnt[i] - 1 : cnt[i]; // 取偶数个
                if (list.isEmpty() && i == 0) continue; // 前导0
                list.add(new int[] {i, n / 2}); // 注意取一半
            } 
        }
        // 开始构造回文串
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < list.size(); i++) {
            int[] t = list.get(i);
            for (int j = 0; j < t[1]; j++) sb.append(t[0]);
        }
        if (mid != -1) sb.append(mid);
        for (int i = list.size() - 1; i >= 0; i--) {
            int[] t = list.get(i);
            for (int j = 0; j < t[1]; j++) sb.append(t[0]);
        }
        // 特判一下空串的情况
        return sb.isEmpty() ? "0" : sb.toString();
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

2385.感染二叉树需要的总时间

题目描述

给你一棵二叉树的根节点 root ，二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟，感染 将会从值为 start 的节点开始爆发。

每分钟，如果节点满足以下全部条件，就会被感染：

节点此前还没有感染。
节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。

示例

输入：root = [1,5,3,null,4,10,6,9,2], start = 3
输出：4
解释：节点按以下过程被感染：

• 第 0 分钟：节点 3
• 第 1 分钟：节点 1、10、6
• 第 2 分钟：节点5
• 第 3 分钟：节点 4
• 第 4 分钟：节点 9 和 2
  感染整棵树需要 4 分钟，所以返回 4 。

思路

图的遍历。使用BFS或者DFS都可以。但注意这道题自己定义了数据结构，导致我们只能从一个节点走到其左右儿子节点，而无法走到该节点的父节点。周赛时我先将题目自己定义的数据结构进行了一下转换（先自己建了下图），然后再从start节点开始进行的遍历。这种思路比较好想，比较简单。当然也可以不建图，直接进行DFS，但那种做法有点不太好想，容易出错。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

/**
* 130ms
**/
class Solution {
    public int amountOfTime(TreeNode root, int start) {
        // 图的邻接表 表示
        Map<Integer, List<Integer>> map = new HashMap<>();
        // 建图
        dfs(root, map);
        Set<Integer> infected = new HashSet<>();
        Queue<Integer> q = new LinkedList<>();
        // 使用BFS
        q.offer(start);
        infected.add(start);
        int ans = 0;
        while (!q.isEmpty()) {
            int size = q.size();
            for (int k = 0; k < size; k++) {
                int x = q.poll();
                for (int i : map.get(x)) {
                    if (infected.contains(i)) continue;
                    q.offer(i);
                    infected.add(i);
                }
            }
            ans++;
        }
        return ans - 1; // 最后一层不需要额外的分钟数
    }

    private void dfs(TreeNode root, Map<Integer, List<Integer>> map) {
        if (root == null) return ;
        if (!map.containsKey(root.val)) map.put(root.val, new ArrayList<>());
        if (root.left != null) {
            map.get(root.val).add(root.left.val);
            if (!map.containsKey(root.left.val)) map.put(root.left.val, new ArrayList<>());
            map.get(root.left.val).add(root.val);
        }
        if (root.right != null) {
            map.get(root.val).add(root.right.val);
            if (!map.containsKey(root.right.val)) map.put(root.right.val, new ArrayList<>());
            map.get(root.right.val).add(root.val);
        }
        dfs(root.left, map);
        dfs(root.right, map);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

现在来尝试一下，只使用给定的数据结构（不自己建图），能否通过一次遍历得到答案。

我自己初步的想法是，利用节点所处位置的深度这一信息。start节点无非3种情况：

• start是根节点
• start在左子树上
• start在右子树上

从根节点开始遍历，依次记录根节点到每个节点的路径长度（深度）。当

• start是根节点，则左右子树中，较大的深度就是答案

• start在左子树上，则看start到根节点的路径长度x，再看根节点右子树的深度r；再看start下面子树的深度l

  答案是max(x + r, l)

• start在右子树上，同理，先看start到根节点的路径长度x，再看根节点左子树的深度l；再看start下面子树的深度r

  答案是max(x + l, r)

------随后发现这样是有点问题的。举个简单的反例

此时start位于根节点的右子树上面，start到根节点的路径长度x = 2，start下面子树的深度为r = 1，根节点左子树的深度l = 1，按照上面的做法，答案是max(x + l, r) = max(2 + 1, 1) = 3；然而由于start这个节点的父节点，即val = 3这个节点，其左子树深度为3，所以最终答案应该是4。

现在俺点开题解，来看看各位人才都是怎么做的。应该是有可以直接从根节点进行遍历的做法。

------看了一圈题解，发现我上面的基本思路没有特别大的问题，但是细节没处理好。比如以上图为样例，start节点为6，答案应该分为两种：

• 以start节点为根节点的子树，其深度

• 从start节点往回走，能走到的最大的深度。

  我们对start节点的每个父节点，都将其作为根节点，进行一下计算即可。

  比如第一次回溯到节点3，将其作为根节点，发现start在根节点的右子树上，则根节点到start的距离x = 1，根节点左子树的深度l = 3，start自身的子树高度r = 1，计算max(x + l, r) = max(1 + 3, 1) = 4；

  再回溯到节点1，将其作为根节点，再进行一下计算。每次取较大者进行更新即可

class Solution {
    int ans = 0;
    int depth = -1; // start节点所处的深度
    public int amountOfTime(TreeNode root, int start) {
        dfs(root, 0, start);
        return ans;
    }

    // level : 当前的深度, start 起始节点, root 当前节点
    // return 当前节点为根节点的子树的深度
    private int dfs(TreeNode root, int level, int start) {
        if (root == null) return 0;
        if (root.val == start) depth = level; // 当前节点就是start
        // 查找左子树
        int l = dfs(root.left, level + 1, start);
        // 查找完左子树后, 看是否有找到start节点
        // 其实inLeft表示start节点为当前节点, 或者在当前节点的左子树上
        boolean inLeft = depth != -1;
        int r = dfs(root.right, level + 1, start);
        if (root.val == start) ans = Math.max(ans, Math.max(l, r)); // 当前节点为start节点, 更新ans
        if (inLeft) ans = Math.max(ans, depth - level + r);
        // 这个else这里root不一定是start的祖先，但不会对答案正确性产生影响
        else ans = Math.max(ans, depth - level + l);
        return Math.max(l, r) + 1; 
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

注意，上面代码的inLeft的含义不一定能保证正确性，但不会影响最终答案。

depth != -1并不能判断当前节点是否是start祖先节点。严格来说根本无法判断当前节点是否是start的祖先节点（无论根据depth!=-1还是depth和当前level的大小关系）。比如start在根节点的左子树上，由于上面代码使用前序遍历，在遍历完根节点左子树后，depth已经!= -1了，此时遍历根节点右子树上的每个节点时，都会因为inLeft=true而错误的认为start节点位于当前节点的左子树上。很明显，根节点的右子树上的所有节点都不是start的祖先节点。（所以此时inLeft的含义是错误的）但由于对右子树上所有节点，计算的depth - level + r ，都不会大于当前节点为根节点时，计算出的depth - level + r，所以不会对答案的正确性产生影响。

-------那么一个比较严谨的思路就是：对整棵树进行DFS遍历，DFS函数返回的是以当前节点为根节点的子树的最大深度，那么

• 若当前节点就是start节点，则用左右子树中的深度较大者，来更新答案
• 若当前节点的左子树上出现了start，则用start节点到当前节点的距离，加上当前节点右子树的深度，来更新答案
• 若当前节点的右子树上出现了start，则用start节点到当前节点的距离，加上当前节点左子树的深度，来更新答案

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int startDepth = -1; // start节点所处的深度
    int ans = 0;
    
    public int amountOfTime(TreeNode root, int start) {
        dfs(root, 0, start);
        return ans;
    }

    private Pair dfs(TreeNode root, int level, int start) {
        if (root == null) return new Pair(0, false);
        boolean exists = false;
        if (root.val == start) {
            exists = true;
            startDepth = level;
        }
        Pair lRes = dfs(root.left, level + 1, start);
        Pair rRes = dfs(root.right, level + 1, start);
        // 当前节点为start节点
        if (root.val == start) ans = Math.max(ans, Math.max(lRes.depth, rRes.depth));
        // 当前节点为根节点的子树中, 是否出现start
        exists = exists || lRes.exists || rRes.exists;
        // 若start出现在左子树上
        if (lRes.exists) ans = Math.max(ans, startDepth - level + rRes.depth);
        // 若start出现在右子树上
        if (rRes.exists) ans = Math.max(ans, startDepth - level + lRes.depth);
        
        int maxDepth = Math.max(lRes.depth, rRes.depth);

        return new Pair(maxDepth + 1, exists);
    }


    class Pair {
        
        public int depth;
        
        public boolean exists;
        
        public Pair (int depth, boolean exists) {
            this.depth = depth;
            this.exists = exists;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

2386. 找出数组的第K大和

题目描述

给你一个整数数组 nums 和一个 正整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。

数组的 第 k 大和 定义为：可以获得的第 k 个 最大 子序列和（子序列和允许出现重复）

返回数组的 第 k 大和 。

子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组，且派生过程不改变剩余元素的顺序。

注意：空子序列的和视作 0 。

思路

先记录一下我自己的思路，虽然没走下去。由于一个子序列是从原先的数组删除某些元素得来的。那么我们可以计算一下所有子序列的个数。

• 删除0个数时：只有1种子序列（从n个数中选0个数，即组合数 $C_n^0$）
• 删除1个数时，共n种子序列（从n个数中选1个数，即组合数 $C_n^1$）
• 删除2个数时，共n × (n - 1) / 2 种子序列（从n个数中选2个数，即组合数 $C_n^2$）
• …
• 删除n个数时，共1种子序列（从n个数中选n个数，即组合数 $C_n^n$）

把全部情况加起来，全部子序列的个数即为：$C_n^0+C_n^1+C_n^2+...+C_n^n=2^n$

这里我想复杂了，其实每个数都有两种选择，保留或删去，一共n个数，每个数有2种可能，那么总的方案数就是 $2^n$

-------只能想到这了。下面看看大佬们的解法。

我们先用类似动态规划的思路来看，设f[i]表示，只考虑[0, i] 区间，这个区间中所有的子序列。即用f[i]表示，[0, i]区间内的所有子序列的方案，我们把这些方案，按照子序列的和从大到小排个序。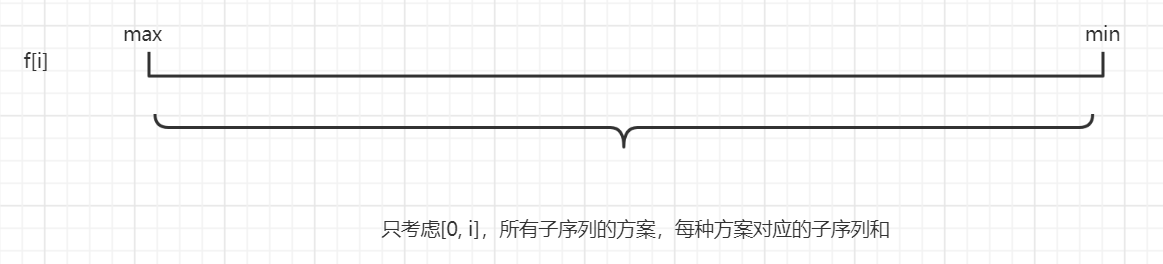

这时我们再来把i + 1这个位置的数加入考虑范围，那么f[i + 1]就是在f[i]的基础上，再多考虑i + 1这个位置的数字。对于i + 1这个位置，只有2种选择，保留它，或删去它。如果是删去它，那么f[i + 1] = f[i]，如果保留它，那么f[i]中的每一种子序列方案中，都需要加上nums[i + 1]，我们画出f[i + 1]的图像，并把它和f[i]放在一起比较，如下

可以看到，在排完序之后，[0, i + 1]中的全部子序列的和，其实就是把[0, i]中的全部子序列的和，平移了一段距离，平移的距离就等于nums[i + 1]的值。注意到上图中的f[i + 1]是保留了nums[i + 1]的情况，而对于删去nums[i + 1]的情况，和f[i] 一致所以就没有画出来（严格来说：f[i + 1]中所有子序列的情况，是上图中2段线段进行合并后的情况）。

由于f[i]中的是已经排好序的，此时我们求解f[i + 1]，只需要将上下两段有序的区间，做一次二路归并操作即可（就是归并排序算法中合并2给区间时的部分逻辑）。合并完之后，得到的区间就是f[i + 1]。如果得到的区间长度大于k，我们可以只保留前k个，因为求解的是前k大，则后续的值不可能作为答案输出。

所以，我们每次能从f[i]转移到f[i + 1]，每次进行归并时，若只保留前k个，则复杂度是$O(k)$。而我们最终需要求得f[n]，一共要求解n个状态，每个状态的复杂度是$O(k)$，那么总的复杂度就是$O(nk)$。

由于n最大值是10^5，而k最大值是2000，那么总的时间复杂度会达到2 × 10^8 级别，我们通常需要将时间复杂度控制在10^7级别内，超过这个级别会有较大概率超时。即便是运算最快的C++，一秒钟能进行的运算也只大概在10^8。所以上面这种做法，是会超时的。我们需要寻找时间复杂度更优秀的算法。

上面这种思路是正向做，是依次把每个数纳入考虑（第一次只考虑第一个数，计算f[0]，第二次纳入第二个数，计算f[1]，…，最后计算f[n-1]），我们可以试试倒着做。倒着做什么意思呢？就是先把数全部加起来。

正着做，顾名思义，是从无到有，从一开始没有数，然后挨个挨个把每个数纳入进来考虑；倒着做，就是一开始就把一些数加起来，得到最大值，然后看看能不能减掉一些数，使得和变小。

我们可以先把最大的和算出来。最大的和怎么算呢？一定是删掉所有负数，保留所有正数的这种方案。

我们先把所有的数，分成三组，分别是：负数、零、正数

子序列的和最大的那种方案，一定是保留全部正数时（或者也可以认为是保留全部正数和0）的方案。我们算出一个最大的和 max。

随后，我们再来考虑，子序列和比这个最大值要小的方案。我们看看如何能把这个最大的和变小：

• 从已经保留了的正数中，删去某个数
• 选择一个负数进行添加
• 零可以并入到上面的第一种情况当中

对于删去一个正数，我们也可以看成加上一个负数；这样就能把所有使得和变小的操作，都看成是加上一个负数。

或者，我们可以把添加一个负数，看成减去一个正数，这样就能把所有使得和变小的操作，都看成是减去一个正数。

我们选择后者，即把所有能使得和变小的操作，都看成是减去一个正数（其实是减去若干个正数，因为一个方案可以选择多个数进行组合）。

那么，假设要求第2大的子序列的和，我们就要从这所有减去一个（若干个）正数的操作中，选出减掉的数最小的那个操作。

我们先将原数组中的负数取个反，变成正数，

然后对所有数从小到大进行一下排序，设排序后的数组为arr。我们需要从这些数中选出若干个数，然后从最大的和中减去被选出的数的和，以此来使得最大的和变小（注意变小的幅度要尽可能的小）。那么很明显，第2大的和，即是从最大和max中，减去arr[0]，那么第3大的和呢？应该是从max中，减去arr[1]；对于第4大的和，则不一定是减去arr[2]了，因为有可能arr[0] + arr[1] < arr[2]，即选择前2个数，能使得下降的幅度更小。

那么问题就变成了，从arr这个数组的前k个数当中进行选择，每个数可以有选或者不选两种情况，组合出来的方案数中，和最小（下降幅度最小）的前k个方案。

问题转变之后，发现和我们一开始的问题是一样的。则可以直接套用我们前面使用动态规划分析出来的方法，前面的思路中，需要计算的状态一共有n个，每种状态计算需要$O(k)$的时间；而我们这样逆着分析后；需要计算的状态一共只有k个了，则总的时间复杂度就变成了$O(k^2)$，而k的最大值为2000，则时间复杂度级别在4 × 10^6，是不会超时的。

class Solution {
    public long kSum(int[] nums, int k) {
        long max = 0, n = nums.length;
        List<Long> arr = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (nums[i] >= 0) {
                max += nums[i]; // 把全部正数加起来
                arr.add((long) nums[i]);
            } else {
                arr.add((long) -nums[i]);// 把负数取反变成正数
            }
        }
        if (k == 1) return max; // 对k=1的情况进行特判, 提前返回
        // 对整个数组从小到大进行排序
        Collections.sort(arr);
        // 计算k个状态, 每次计算需要进行二路归并, 所以需要开2个数组
        List<Long> a = new ArrayList<>();
        List<Long> b = new ArrayList<>();
        // 只需要用到arr数组中的前k个数字, 即, 只会计算f[0] ~ f[k - 1]
        // 每一次迭代时, 计算出来的f其实就是合并后的数组a
        int end = Math.min(k - 1, arr.size() - 1);
        // max 是第一大的和
        // 只选一个数时, 有两种方案, 选或者不选, 不选时, arr的第一个元素对应就是最大的和
        // 初始化f[0], 只考虑第一个数时, 有两种方案, 选或者不选
        a.add(0L); // 不选第一个数, 和就是max, 是第1大和
        a.add(arr.get(0)); // 选第一个数, 是第2大和
        // 迭代计算 f[1] ~ f[k - 1]
        for (int p = 1; p <= end; p++) {
            long x = arr.get(p);
            int i = 0, j = 0;
            int maxLen = 2 * a.size(); // 二路归并最多会有2倍的size大小
            int finalLen = Math.min(maxLen, k); // 归并的结果只需要保留前k个
            // 把二路归并的结果放在b当中
            while (i < a.size() && j < a.size() && b.size() < finalLen) {
                if (a.get(i) <= a.get(j) + x) b.add(a.get(i++));
                else b.add(a.get(j++) + x);
            }
            // 把剩余的加上
            while (i < a.size() && b.size() < finalLen) b.add(a.get(i++));
            while (j < a.size() && b.size() < finalLen) b.add(a.get(j++) + x);
            // 交换a和b
            List<Long> t = a;
            a = b;
            b = t;
            // 清空b
            b.clear();
        }
        return max - a.get(k - 1);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

总结

还不错，3题，心满意足。继续加油！