备战数学建模38-粒子群算法pso番外篇1(攻坚战2)

粒子群算法的思想源于对鸟群捕食行为的研究，模拟鸟集群飞行觅食的行为，鸟之间通过集体的协作使群体达到最优目的，是一种基于Swarm Intelligence的优化方法。马良教授在他的著作《蚁群优化算法》一书的前言中写到：自然界中的蚁群，鸟群，鱼群，羊群，牛群，蜂群等都时时刻刻在给与我们某种启示，只不过我们往往忽略了大自然给予我们的最大的恩赐。

一、粒子群算法番外篇1

1.1、粒子群算法简介

1.2、粒子群算法的符号说明与基本流程

1.3、粒子群算法求一元函数的最大值

1.4、粒子群算法求二元函数的最小值

1.5、三种改变惯性权重优化粒子群算法的方法

1.6、改变因子优化粒子群算法的方法

1.7、Matlab自带的粒子群函数

1.8、案例总结

一、粒子群算法番外篇1

1.1、粒子群算法简介

粒子群算法最初是根据鸟类群体行为得到的启发，对鸟群行为进行仿真的算法，是一种启发式算法，也就是智能优化算法，利用信息共享，通过中间信息进行改进搜索，从而获得问题的可行解。

我们简单从下图去体会一下粒子群算法，就是有多个鸟，每个鸟相当于一个粒子，每只鸟的位置受自己认知的历史最佳位置和当前距离食物最近的鸟的位置的影响。

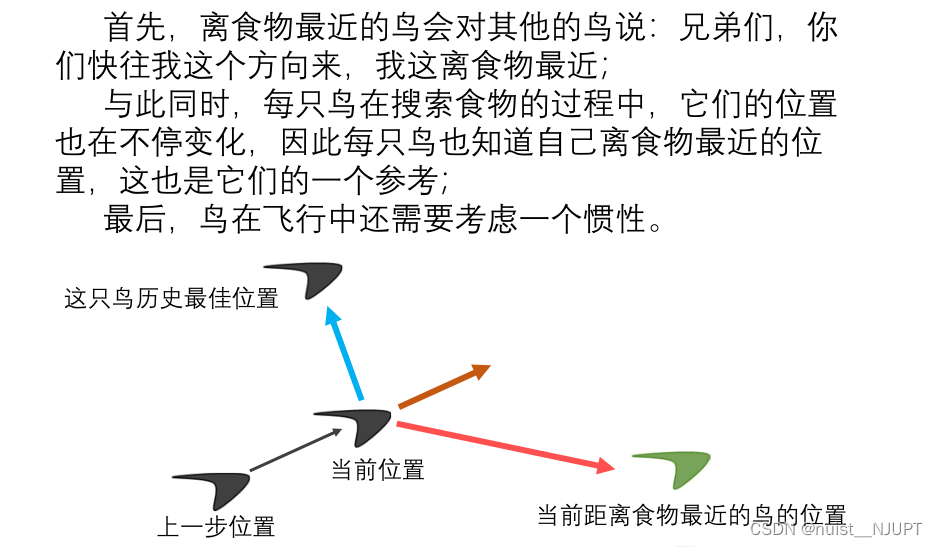
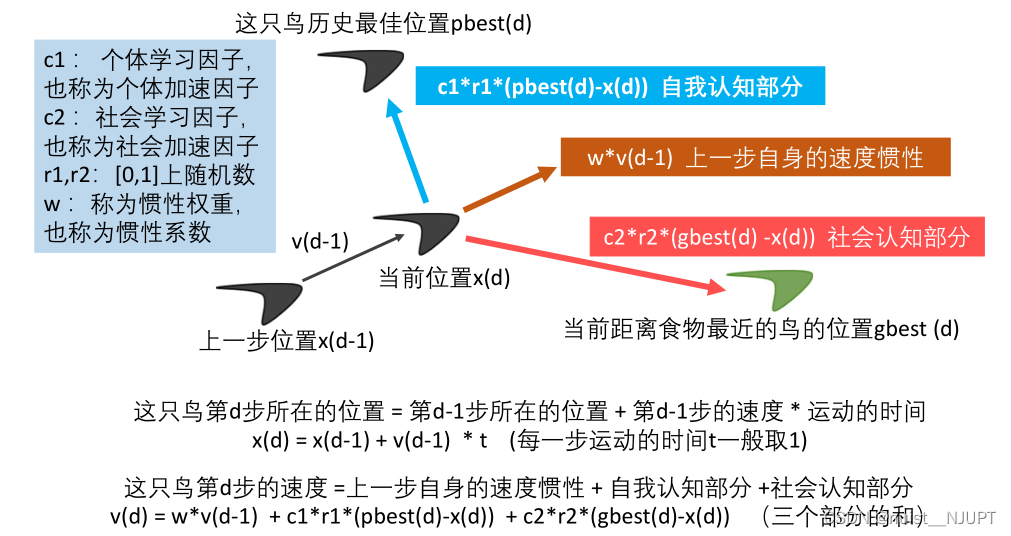
我们进一步分析这个图，可以得到两个公式，第一个是速度公式，即每只鸟的当前速度受上一步的速度惯性，自我认知和社会认知三部分影响，第二个是位置公式，即每只鸟的位置受上一位置和上一位置的速度的影响。

1.2、粒子群算法的符号说明与基本流程

1）例子群算法6个基本概念如下：

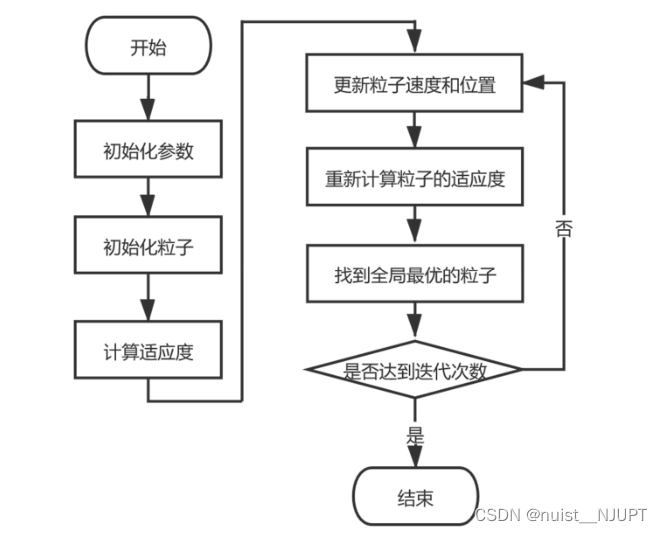
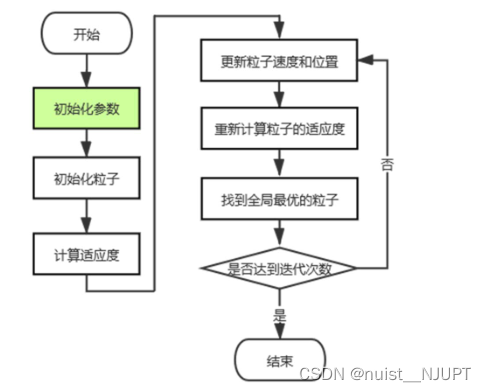
2）粒子群算法的流程图如下，总的来说，就是在一个给定的范围内，不停地迭代，直到找到一个最优的可行解，即全局最优粒子。

3）粒子群算法涉及的主要符号如下，这是根据公式给出的。

4）粒子群算法的核心公式如下：本质上就两个核心公式，就是速度和位置，通过不停的更新粒子的速度和位置，找到最适应的位置，即求出全局最优粒子。

最初提出的粒子群算法中，一般粒子群的个体学习因子c1和社会学习因子c2取2比较合适。

而惯性因子w一般取0.9~1.2比较合适。

1.3、粒子群算法求一元函数的最大值

比如：我们打算求解如下一元函数的在指定区间的内的最值，我们可以采用传统的方法实现，这边也可以使用粒子群算法实现，具体如下：

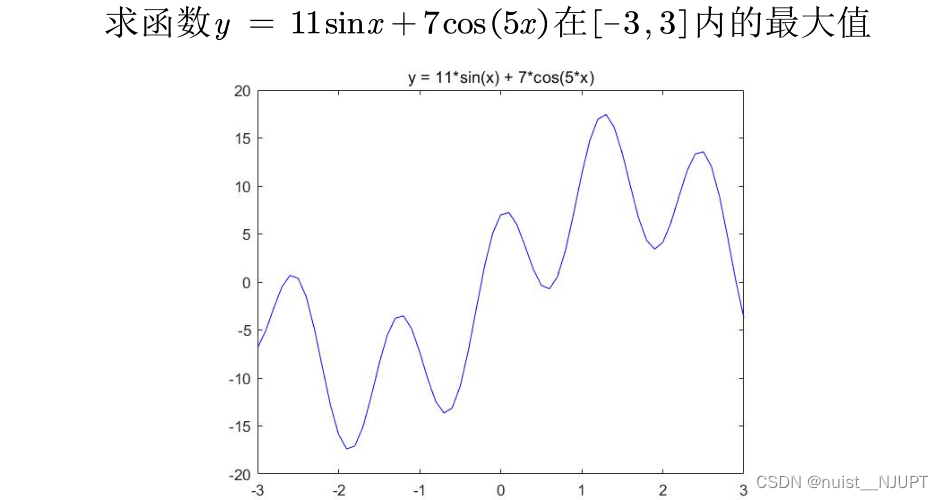
Matlab使用传统的求极值方法，求解函数的极值，其实这种求解方法对初始值的选取要求很高，如果初始值x0不取0，很有可能陷入局部最优解，具体如下：jam


function y = f(x)
y = - (11*sin(x)+7*cos(5*x));
end


clc
clear 
x0 = 0 ;
%线性不等式约束
A = [] ;
b = [] ;
%线性等式约束
Aeq = [] ;
beq = [] ;
x_lb = -3 ; %下界
x_ub = 3 ; %上届
[x,fval] = fmincon(@f,x0,A,b,Aeq,beq,x_lb,x_ub) ;
fval = -fval ;
disp(x) ;
disp(fval) ;

运行结果如下：

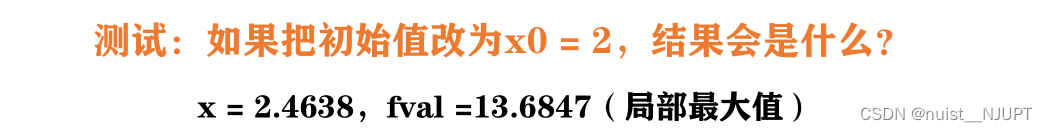
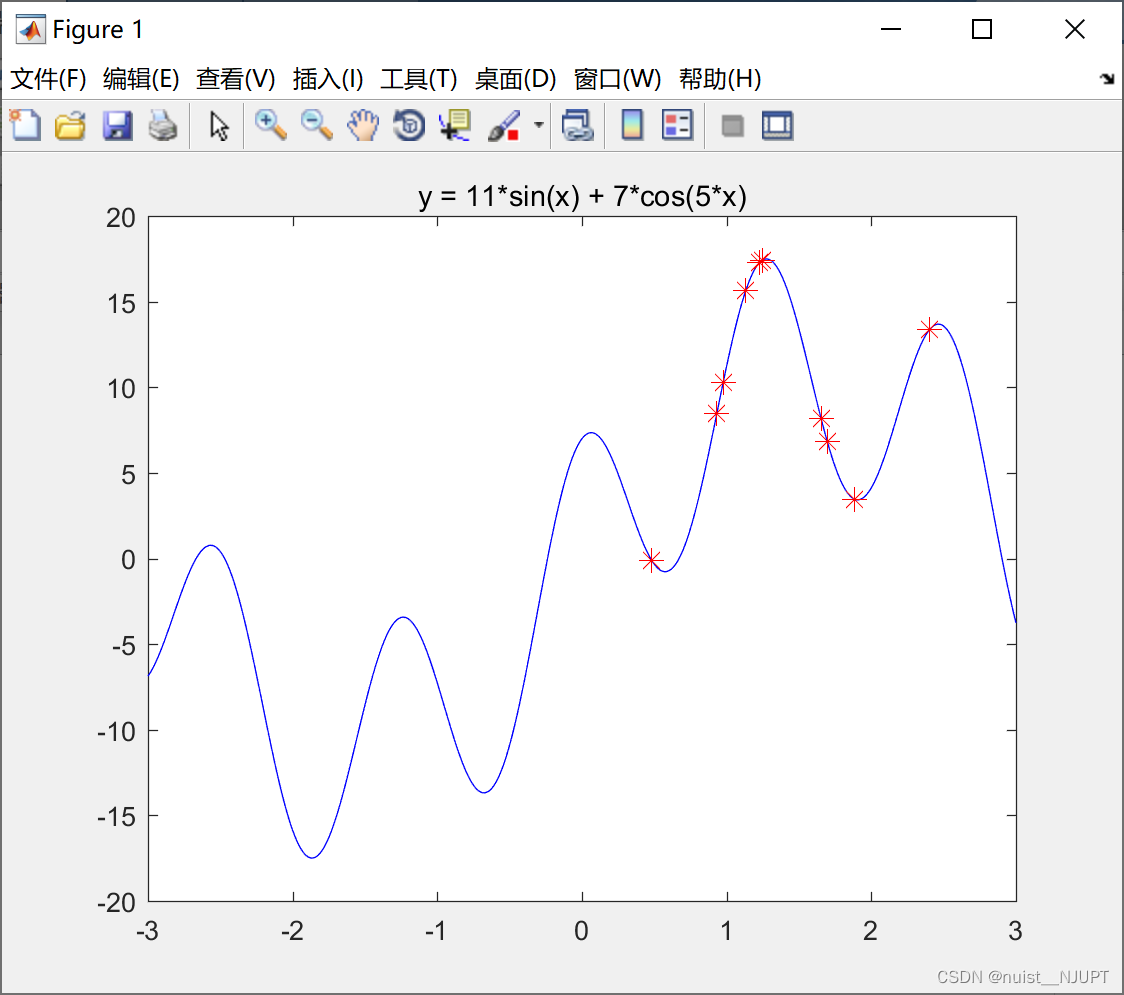
下面使用粒子群算法求解该函数的极大值，如下：

(1) 增加粒子数量会增加我们找到更好结果的可能性，但会增加运算的时间。
(2) c1,c2,w这三个量有很多改进空间，未来我再来专门讲怎么去调整。
(3) 迭代的次数K越大越好吗？不一定哦，如果现在已经找到最优解了，再增加迭代次数是没有意义的。
(4) 这里出现了粒子的最大速度，是为了保证下一步的位置离当前位置别太远，一般取自变
量可行域的10%至20%(不同文献看法不同)。
(5) X的下界和上界是保证粒子不会飞出定义域。

(6)设置的相关参数如下，粒子的数量n = 10; ，每个粒子的个体学习因子c1 = 2;每个粒子的社会学习因子c2 = 2; 惯性权重w = 0.9;迭代的次数K = 50。

整个执行过程如下：

运行的效果如下：

粒子群全局寻优Matlab代码如下：


close all
clc
clear
%绘制函数的图形
x = -3:0.01:3;
y = 11*sin(x) + 7*cos(5*x);
figure(1)
plot(x,y,'b-')
title('y = 11*sin(x) + 7*cos(5*x)')
hold on  % 不关闭图形，继续在上面画图
 
 
%参数定义部分
num = 1 ; %变量个数
n = 10 ;%粒子数量
c1 = 2 ; %学习因子
c2 = 2 ; %社会因子
w = 0.9 ; %惯性权重
k = 50; %最大迭代次数
vmax = 1.2 ; %粒子的最大速度
%x的上下界
x_lb = -3 ;
x_ub = 3 ;
gbest = 0;
 
%初始化粒子的位置和速度
x = zeros(n,num) ;
for i = 1 : num 
    %随机初始化粒子所在的位置在定义域内
    x(:,i) = x_lb(i) + (x_ub - x_lb) * rand(n,1) ;
end
%随机初始化粒子的速度，在[-vmax,vmax]之间
v = -vmax + 2*vmax.*rand(n,num) ;
 
%计算粒子适应度
fit = zeros(n,1) ; %初始化适应度
for i = 1 : n
    fit(i) = f(x(i,:)) ; %调用函数f计算粒子的适应度
end
 
pbest = x ; %初始化粒子的最佳位置
index= find(fit ==max(fit),1) ; %找到适应度最大的粒子下标
gbest = x(index,:) ; %找到所有粒子的目前最佳位置
 
h = scatter(x,fit,80,'*r'); %绘制散点图,用于演示
%更新粒子的速度和位置
for d = 1 :  k 
    for i = 1 : n 
        %更新第i个粒子的速度
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));
        %如果粒子的速度超过最大值，需要进行限制
        for j = 1: num
            if v(i,j) < -vmax(j)
               v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
               v(i,j) = vmax(j);
            end
        end
            x(i,:) = x(i,:) + v(i,:) ; %更新第i个粒子的位置
            %如果粒子的位置超过最大值，需要限制
            for j = 1: num
                if x(i,j) < x_lb(j)
                    x(i,j) = x_lb(j);
                 elseif x(i,j) > x_ub(j)
                    x(i,j) = x_ub(j);
                end
            end
            %重新计算适应度并找到最优粒子
            fit(i) = f(x(i,:)); % 重新计算第i个粒子的适应度
            % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
            if fit(i) > f(pbest(i,:))
                  pbest(i,:) = x(i,:); % 更新第i个粒子迄今为止找到的最佳位置
            end
            % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            if f(pbest(i,:)) > f(gbest)
                 gbest = pbest(i,:); % 更新所有粒子迄今为止找到的最佳位置
            end
    end
    fitnessbest(d) = f(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x;  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = fit; % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
end
% 绘制出每次迭代最佳适应度的变化图
figure(2)
plot(fitnessbest) 
xlabel('迭代次数');
ylabel('适应度') ;
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(f(gbest))

所用的适应度函数如下：


function y = f(x)
y = 11*sin(x)+7*cos(5*x);
end

1.4、粒子群算法求二元函数的最小值

求二元函数的最小值和前面的思路一样，只是变成了三维，还有就是变成最小值，那就是每次得到适应度函数的最小值即可。设置的初始化参数如下：粒子数量n = 30; 变量个数narvs = 2;
每个粒子的个体学习因子c1 = 2; 每个粒子的社会学习因子c2 = 2; 惯性权重w = 0.9; 迭代的次数K = 100。

Matlab实现的代码如下所示：


% 粒子群算法
clear; clc
 
% 绘制函数的图形
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1');  ylabel('x2');  zlabel('y');  % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on  % 不关闭图形
 
% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 100;  % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
 
% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);    % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）
 
% 计算适应度(注意，因为是最小化问题，所以适应度越小越好)
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun2(x(i,:));   % 调用Obj_fun2函数来计算适应度
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == min(fit), 1);  % 找到适应度最小的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）
 
% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:,1),x(:,2),fit,'*r');  % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
 
% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun2(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) < Obj_fun2(pbest(i,:))   % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
           pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) < Obj_fun2(gbest)  % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun2(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x(:,1);  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = x(:,2);   % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
    h.ZData = fit;  % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end
 
figure(2) 
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
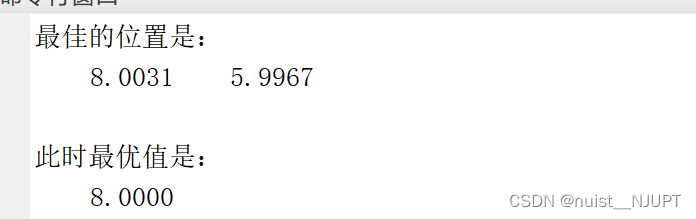
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun2(gbest))

适应度函数如下：


function y = Obj_fun2(x)  
% y = x1^2+x2^2-x1*x2-10*x1-4*x2+60
% x是一个向量哦！
    y = x(1)^2 + x(2)^2 - x(1)*x(2) - 10*x(1) - 4*x(2) + 60; % 千万别写成了x1
end

运行的结果如下：

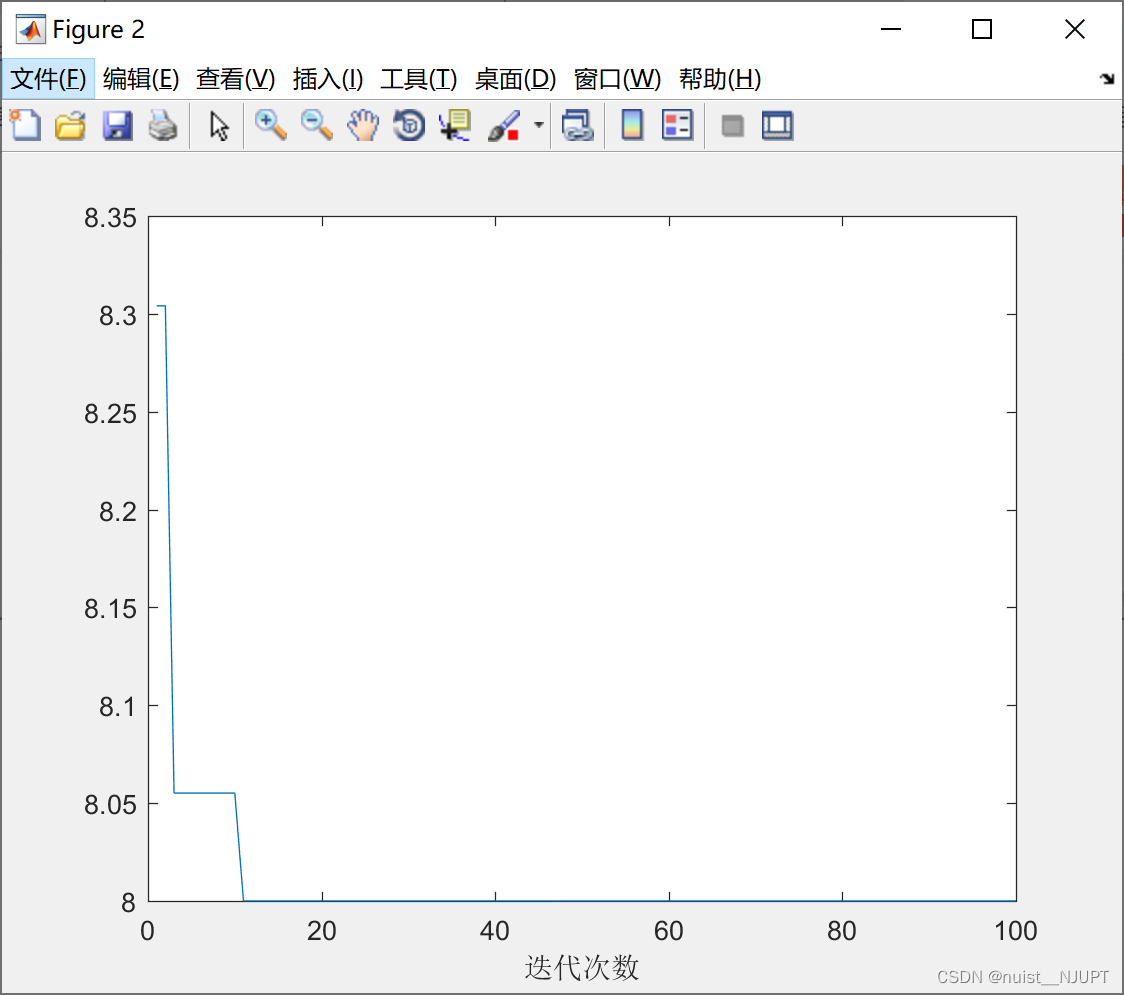
1.5、三种改变惯性权重优化粒子群算法的方法

1）方法1：线性递减权重法，前期应该让粒子群全局搜索，故权重w应该大一些，后面应该局部搜索寻找最优解，故应该使关性权重小一些。

对于上述的求解二元函数最值问题，使用线性递减权重法优化后的代码如下：


% 粒子群算法
clear; clc
 
% 绘制函数的图形
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1');  ylabel('x2');  zlabel('y');  % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on  % 不关闭图形
 
% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 100;  % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
w_start = 0.9;  % 初始惯性权重，通常取0.9
w_end = 0.4; % 粒子群最大迭代次数时的惯性权重，通常取0.4
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
 
% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);    % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）
 
% 计算适应度(注意，因为是最小化问题，所以适应度越小越好)
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun2(x(i,:));   % 调用Obj_fun2函数来计算适应度
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == min(fit), 1);  % 找到适应度最小的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）
 
% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:,1),x(:,2),fit,'*r');  % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
 
% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
         w = w_start - (w_start - w_end) * d / K;  
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun2(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) < Obj_fun2(pbest(i,:))   % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
           pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) < Obj_fun2(gbest)  % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun2(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x(:,1);  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = x(:,2);   % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
    h.ZData = fit;  % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end
 
figure(2) 
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun2(gbest))

适应度函数的代码：


function y = Obj_fun2(x)  
% y = x1^2+x2^2-x1*x2-10*x1-4*x2+60
% x是一个向量哦！
    y = x(1)^2 + x(2)^2 - x(1)*x(2) - 10*x(1) - 4*x(2) + 60; % 千万别写成了x1
end

2）方法2：自适应惯性权重改进pso的方法，我们可以知道惯性越大，越利于全局搜索，反之，越利于局部搜索，对于求最小值问题，当适应度越小，我们需要局部搜索；适应度越大，我们需要全局搜索，故根据当前适应度和平均值适应度的关系，自适应改变惯性权重。

“

对于求解最大值问题，则和最小值刚好相反，适应度小，则应该全局搜索，适应度大，则应该局部送搜索，找到最优解。

对于上面的求解二元函数极值问题，使用自适应惯性权重进行优化，代码如下：


% 粒子群算法
clear; clc
 
% 绘制函数的图形
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1');  ylabel('x2');  zlabel('y');  % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on  % 不关闭图形
 
% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2;  % 每个粒子的社会学习因子，也称为社会加速常数
w = 0.9;  % 惯性权重
K = 100;  % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
w_max = 0.9;  % 最大惯性权重，通常取0.9
w_min = 0.4; % 最小惯性权重，通常取0.4
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
 
% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);    % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）
 
% 计算适应度(注意，因为是最小化问题，所以适应度越小越好)
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun2(x(i,:));   % 调用Obj_fun2函数来计算适应度
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == min(fit), 1);  % 找到适应度最小的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）
 
% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:,1),x(:,2),fit,'*r');  % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
 
% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        f_i = fit(i);  % 取出第i个粒子的适应度
        f_avg = sum(fit)/n;  % 计算此时适应度的平均值
        f_min = min(fit); % 计算此时适应度的最小值
        if f_i <= f_avg  
            if f_avg ~= f_min  % 如果分母为0，我们就干脆令w=w_min
                w = w_min + (w_max - w_min)*(f_i - f_min)/(f_avg - f_min);
            else
                w = w_min;
            end
        else
            w = w_max;
        end
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
  
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun2(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) < Obj_fun2(pbest(i,:))   % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
           pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) < Obj_fun2(gbest)  % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun2(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x(:,1);  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = x(:,2);   % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
    h.ZData = fit;  % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end
 
figure(2) 
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun2(gbest))

sdhdfwe-fe发付文锋给

3）方法3：随机惯性权重法优化pso，就是随机产生一个权重，使用随机的惯性权重，可以避免在迭代前期局部搜索能力的不足；也可以避免在迭代后期全局搜索能力的不足。代码省略了。就加一行随机产生w就可以。

1.6、改变因子优化粒子群算法的方法

1）方法1：压缩(收缩)因子法，个体学习因子c1和社会(群体)学习因子c2决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响，其反映了粒子群之间的信息交流。设置c1较大的值，会使粒子过多地在自身的局部范围内搜索，而较大的c2的值，则又会促使粒子过早收敛到局部最优值。为了有效地控制粒子的飞行速度，使算法达到全局搜索与局部搜索两者间的有效平衡，Clerc构造了引入收缩因子的PSO模型，采用了压缩因子，这种调整方法通过合适选取参数，可确保PSO算法的收敛性，并可取消对速度的边界限制。

还是使用该方法对上述的求二元函数最值问题进行优化，MATLAB代码如下，本质上就是在速度之前加一个收缩因子进行限制，如下：


% 粒子群算法
clear; clc
 
% 绘制函数的图形
x1 = -15:1:15;
x2 = -15:1:15;
[x1,x2] = meshgrid(x1,x2);
y = x1.^2 + x2.^2 - x1.*x2 - 10*x1 - 4*x2 + 60;
mesh(x1,x2,y)
xlabel('x1');  ylabel('x2');  zlabel('y');  % 加上坐标轴的标签
axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
hold on  % 不关闭图形
 
% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 30; % 粒子数量
narvs = 2; % 变量个数
c1 = 2.05;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2.05;  % 每个粒子的社会学习因子，也称为社会加速常数
C = c1+c2; 
fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子
w = 0.9;  % 惯性权重
K = 100;  % 迭代的次数
vmax = [6 6]; % 粒子的最大速度
w_max = 0.9;  % 最大惯性权重，通常取0.9
w_min = 0.4; % 最小惯性权重，通常取0.4
x_lb = [-15 -15]; % x的下界
x_ub = [15 15]; % x的上界
 
% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);    % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）
 
% 计算适应度(注意，因为是最小化问题，所以适应度越小越好)
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun2(x(i,:));   % 调用Obj_fun2函数来计算适应度
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == min(fit), 1);  % 找到适应度最小的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）
 
% 在图上标上这n个粒子的位置用于演示
h = scatter3(x(:,1),x(:,2),fit,'*r');  % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
 
% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        f_i = fit(i);  % 取出第i个粒子的适应度
        f_avg = sum(fit)/n;  % 计算此时适应度的平均值
        f_min = min(fit); % 计算此时适应度的最小值
        if f_i <= f_avg  
            if f_avg ~= f_min  % 如果分母为0，我们就干脆令w=w_min
                w = w_min + (w_max - w_min)*(f_i - f_min)/(f_avg - f_min);
            else
                w = w_min;
            end
        else
            w = w_max;
        end
         v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)));  % 更新第i个粒子的速度
  
  
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun2(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) < Obj_fun2(pbest(i,:))   % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
           pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) < Obj_fun2(gbest)  % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun2(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x(:,1);  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
    h.YData = x(:,2);   % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
    h.ZData = fit;  % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end
 
figure(2) 
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun2(gbest))

2）方法2：非对称学习因子优化粒子群算法，随着迭代的增加急，线性的增加c1,减小c2，增加粒子向着全局最优点收敛的能力。代码略。

1.7、Matlab自带的粒子群函数

matlab拥有自带的粒子群函数particleswarm，该函数的优化效果特别好，这样就不需要自己写大量的循环和判断语句了。该函数采用的是自适应邻域模式。

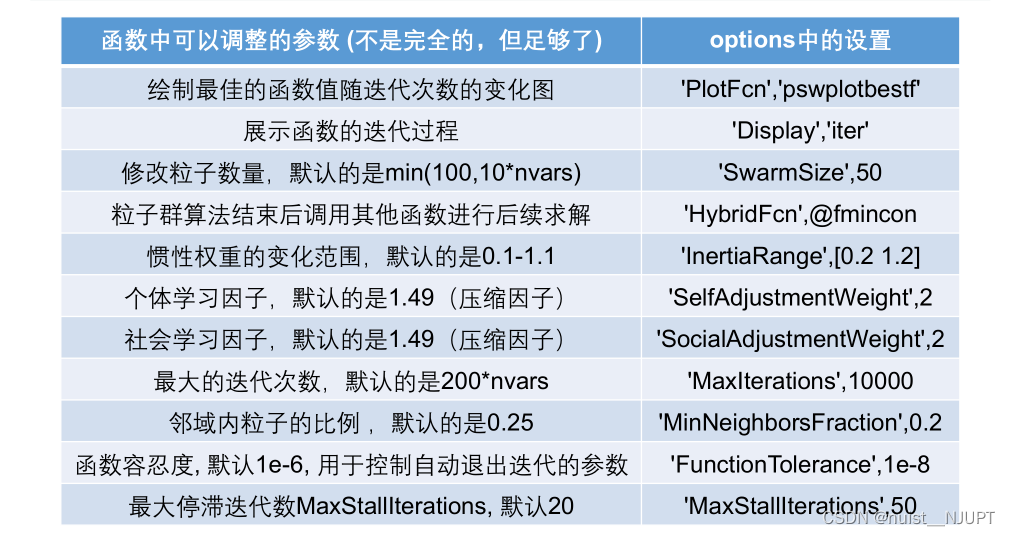
使用这个函数我们同样需要进行一些参数的预设，主要需要设置粒子个数，惯性权重，学习因子以及邻域内的粒子比例。

另外我们需要对速度和位置变量进行初始化，同时需要计算粒子的适应度，同时计算个体最优位置和所有粒子的最优位置。

使用matlab自带的粒子群函数求解，一般会需要进行函数中参数的调整，options中的设置如下：

1）matlab自带的粒子群函数求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值（最小值为8）


% Matlab自带的粒子群函数 particleswarm
% particleswarm函数是求最小值的
% 如果目标函数是求最大值则需要添加负号从而转换为求最小值。
clear;clc
 
% 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值（最小值为8）
narvs = 2; % 变量个数
x_lb = [-15 -15]; % x的下界(长度等于变量的个数，每个变量对应一个下界约束)
x_ub = [15 15]; % x的上界
[x,fval,exitflag,output] = particleswarm(@Obj_fun2, narvs, x_lb, x_ub)   
 
 
% 绘制最佳的函数值随迭代次数的变化图
options = optimoptions('particleswarm','PlotFcn','pswplotbestf')   
[x,fval] = particleswarm(@Obj_fun2,narvs,x_lb,x_ub,options)
 
% 展示函数的迭代过程
options = optimoptions('particleswarm','Display','iter');
[x,fval] = particleswarm(@Obj_fun2,narvs,x_lb,x_ub,options)


function y = Obj_fun2(x)  
% y = x1^2+x2^2-x1*x2-10*x1-4*x2+60
% x是一个向量哦！
    y = x(1)^2 + x(2)^2 - x(1)*x(2) - 10*x(1) - 4*x(2) + 60; % 千万别写成了x1
end

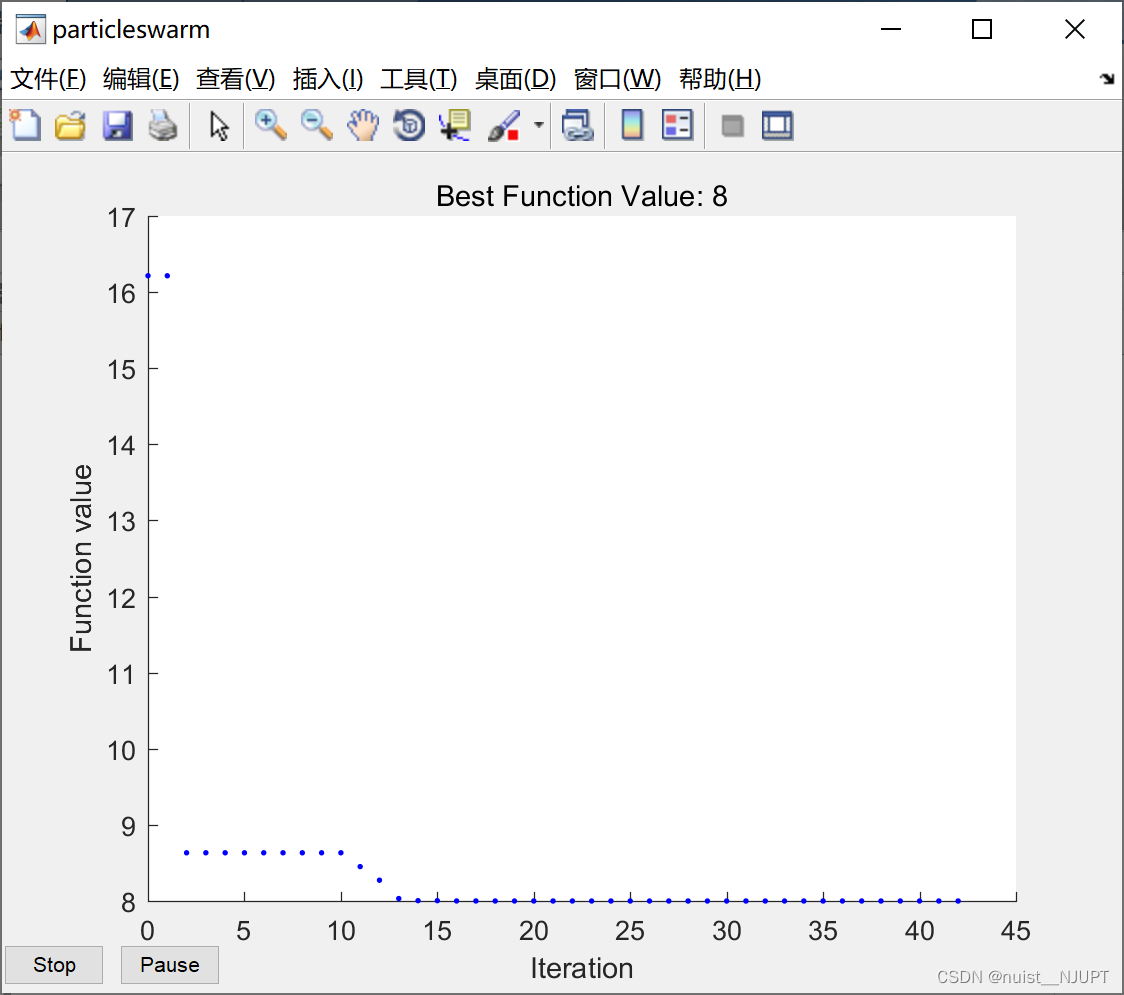
2）下面使用matlab自带的粒子群函数对如下第二个自适应函数进行测试，代码如下：


% Matlab自带的粒子群函数 particleswarm
% particleswarm函数是求最小值的
% 如果目标函数是求最大值则需要添加负号从而转换为求最小值。
clear;clc
 
%% 直接调用particleswarm函数进行求解测试函数
narvs = 30; % 变量个数
% Sphere函数
% x_lb = -100*ones(1,30); % x的下界
% x_ub = 100*ones(1,30); % x的上界
% Rosenbrock函数
x_lb = -30*ones(1,30); % x的下界
x_ub = 30*ones(1,30); % x的上界
% Rastrigin函数
% x_lb = -5.12*ones(1,30); % x的下界
% x_ub = 5.12*ones(1,30); % x的上界
% Griewank函数
% x_lb = -600*ones(1,30); % x的下界
% x_ub = 600*ones(1,30); % x的上界
[x,fval,exitflag,output] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub)  
 
 
%% 绘制最佳的函数值随迭代次数的变化图
options = optimoptions('particleswarm','PlotFcn','pswplotbestf')   
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 展示函数的迭代过程
options = optimoptions('particleswarm','Display','iter');
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 修改粒子数量，默认的是：min(100,10*nvars)
options = optimoptions('particleswarm','SwarmSize',50);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 在粒子群算法结束后继续调用其他函数进行混合求解（hybrid  n.混合物合成物; adj.混合的; 杂种的;） 
options = optimoptions('particleswarm','HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 惯性权重的变化范围，默认的是0.1-1.1
options = optimoptions('particleswarm','InertiaRange',[0.2 1.2]);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 个体学习因子，默认的是1.49（压缩因子）
options = optimoptions('particleswarm','SelfAdjustmentWeight',2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 社会学习因子，默认的是1.49（压缩因子）
options = optimoptions('particleswarm','SocialAdjustmentWeight',2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 最大的迭代次数，默认的是200*nvars
options = optimoptions('particleswarm','MaxIterations',10000);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 领域内粒子的比例 MinNeighborsFraction，默认是0.25 
options = optimoptions('particleswarm','MinNeighborsFraction',0.2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 函数容忍度FunctionTolerance, 默认1e-6, 用于控制自动退出迭代的参数
options = optimoptions('particleswarm','FunctionTolerance',1e-8);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 最大停滞迭代数MaxStallIterations, 默认20, 用于控制自动退出迭代的参数
options = optimoptions('particleswarm','MaxStallIterations',50);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
 
%% 不考虑计算时间，同时修改三个控制迭代退出的参数
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',100000);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
toc
 
%% 在粒子群结束后调用其他函数进行混合求解
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',50,'MaxIterations',20000,'HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
toc

蚁wen群


function y = Obj_fun3(x)
% 注意，x是一个向量
% Sphere函数
%     y = sum(x.^2);  % x.^2 表示x中每一个元素分别计算平方
 
% Rosenbrock函数
    tem1 = x(1:end-1);  
    tem2 = x(2:end);
    y = sum(100 * (tem2-tem1.^2).^2 + (tem1-1).^2);
 
% Rastrigin函数
%     y = sum(x.^2-10*cos(2*pi*x)+10);
 
% Griewank函数
%     y = 1/4000*sum(x.*x)-prod(cos(x./sqrt(1:30)))+1;
end

1.8、案例总结

对于如下的函数，使用三种方法求这个函数的最大值，第一种方法是使用fmincon函数，第二种方法是自己手写粒子群函数，第三种方法是调用matlab自带的粒子群函数。

方法1的matlab代码：


%% 求解函数y = 21.5+x(1)*sin(4*pi*x(1))+x(2)*sin(20*pi*x(2))在x1属于[-3,12.1]，x2属于[4.1,5.8]内的最大值
% 目标函数参考的最优值：38.8503    
x0 =  [11.6 5.7];  % 这里的初始值如果取得偏离一点，结果就可能千差万别
% 不要问我为啥会选择这一个初始值，我是站在上帝视角选择的~~~
A=[]; b=[];
Aeq=[];beq=[];
x_lb = [-3 4.1]; % x的下界
x_ub = [12.1 5.8]; % x的上界
[x,fval] = fmincon(@Obj_fun_1,x0,A,b,Aeq,beq,x_lb,x_ub)
fval = -fval


function y = Obj_fun_1(x)
     y =- (21.5 + x(1)*sin(4*pi*x(1)) + x(2)*sin(20*pi*x(2)));  
     % 如果调用fmincon函数或者particleswarm函数，则需要添加负号改为求最小值
end

方法2的matlab代码：使用了自使用的权重系数进行优化，也使用了收缩因子对速度进行限制。


%% 综合应用：粒子群算法PSO: 求解函数y = 21.5+x(1)*sin(4*pi*x(1))+x(2)*sin(20*pi*x(2))在x1属于[-3,12.1]，x2属于[4.1,5.8]内的最大值(动画演示）
clear; clc   % 目标函数参考的最优值：38.8503    
 
%% 绘制函数的图形
% x1 = -3:0.01:12.1;
% x2 = 4.1:0.01:5.8;
% [x1,x2] = meshgrid(x1,x2);
% y = 21.5 + x1.*sin(4*pi*x1) + x2.*sin(20*pi*x2);
% mesh(x1,x2,y)
% xlabel('x1');  ylabel('x2');  zlabel('y');  % 加上坐标轴的标签
% axis vis3d % 冻结屏幕高宽比，使得一个三维对象的旋转不会改变坐标轴的刻度显示
% hold on  % 不关闭图形，继续在上面画图
 
%% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 1000; % 粒子数量
narvs = 2; % 变量个数
c1 = 2.05;  % 每个粒子的个体学习因子，也称为个体加速常数
c2 = 2.05;  % 每个粒子的社会学习因子，也称为社会加速常数
C = c1+c2; 
fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子
w_max = 0.9;  % 最大惯性权重，通常取0.9
w_min = 0.4; % 最小惯性权重，通常取0.4
K = 100;  % 迭代的次数
vmax = [1.51 0.17]; % 粒子的最大速度
x_lb = [-3 4.1]; % x的下界
x_ub = [12.1 5.8]; % x的上界
 
%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
    x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1);    % 随机初始化粒子所在的位置在定义域内
end
v = -repmat(vmax, n, 1) + 2*repmat(vmax, n, 1) .* rand(n,narvs);     % 随机初始化粒子的速度（这里我们设置为[-vmax,vmax]）
 
%% 计算适应度
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun_2(x(i,:));   % 调用Obj_fun_2函数来计算适应度
end 
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == max(fit), 1);  % 找到适应度最大的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）
 
%% 在图上标上这n个粒子的位置用于演示
% h = scatter3(x(:,1),x(:,2),fit,'*r');  % scatter3是绘制三维散点图的函数（这里返回h是为了得到图形的句柄，未来我们对其位置进行更新）
 
%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        f_i = fit(i);  % 取出第i个粒子的适应度
        f_avg = sum(fit)/n;  % 计算此时适应度的平均值
        f_max = max(fit); % 计算此时适应度的最大值
        if f_i >= f_avg  
             if f_avg ~= f_max  % 如果分母为0，我们就干脆令w=w_min
                w = w_min + (w_max - w_min)*(f_max - f_i)/(f_max - f_avg);
            else
                w = w_min;
             end
        else
            w = w_max;
        end
        v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:)));  % 更新第i个粒子的速度
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun_2(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) > Obj_fun_2(pbest(i,:))   % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
           pbest(i,:) = x(i,:);   % 那就更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) > Obj_fun_2(gbest)  % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 那就更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun_2(gbest);  % 更新第d次迭代得到的最佳的适应度
%     pause(0.1)  % 暂停0.1s
%     h.XData = x(:,1);  % 更新散点图句柄的x轴的数据（此时粒子的位置在图上发生了变化）
%     h.YData = x(:,2);   % 更新散点图句柄的y轴的数据（此时粒子的位置在图上发生了变化）
%     h.ZData = fit;  % 更新散点图句柄的z轴的数据（此时粒子的位置在图上发生了变化）
end
 
figure(2) 
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun_2(gbest))


function y = Obj_fun_2(x)  
% x是一个向量哦！
    y = (21.5 + x(1)*sin(4*pi*x(1)) + x(2)*sin(20*pi*x(2)));
end

方法3的matlab代码:


% 目标函数参考的最优值：38.8503    
narvs = 2; % 变量个数
x_lb = [-3 4.1]; % x的下界
x_ub = [12.1 5.8]; % x的上界
 
%% 直接使用particleswarm函数
[x,fval] = particleswarm(@Obj_fun_1,narvs,x_lb,x_ub)
fval = -fval
 
%% 将粒子群算法得到的解作为初始值，继续调用fmincon函数求解
options = optimoptions('particleswarm','HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun_1,narvs,x_lb,x_ub,options)
fval = -fval
 
%% 修改参数：这里要增加粒子个数，因为函数局部最小值太多了
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',20000,'SwarmSize',1000);
[x,fval] = particleswarm(@Obj_fun_1,narvs,x_lb,x_ub,options)
fval = -fval

、群群、牛群、蜂群等，其实时时刻刻都在wedew时刻我们以某种启示，只不过我们常常忽大恩赐！......”

相关阅读:
React报错之JSX element type does not have any construct or call signatures
CSS绘制各种三角形
 JVM下篇(一、性能监控与调优-概述篇)
c语言实现http下载功能，显示进度条和下载速率
 产业园区中工业厂房的能源综合配置
 Xcode 清空最近打开的项目
 分页插件(分页插件的使用、通过分页插件获取分页相关数据)
nginx常用命令
 Spring Security 自定义用户信息端点与多种登录方式共存
 学习太极创客 — MQTT（七）MQTT 主题进阶
原文地址：https://blog.csdn.net/nuist_NJUPT/article/details/126694074