-
有限元编程示例
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档
前言
本文内容大部分来自b站的博主易木木响叮当的视频
还有就是参考曾攀老师《有限元基础教程》这本书
一、1D 三连杆结构的有限元分析过程
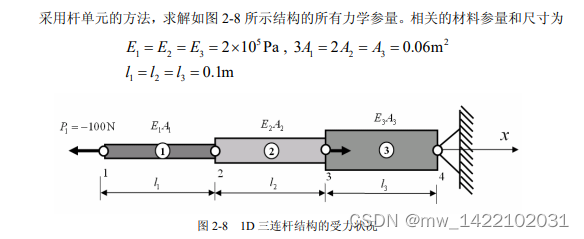
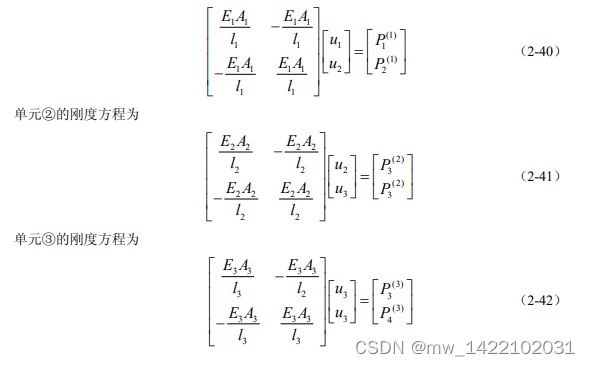
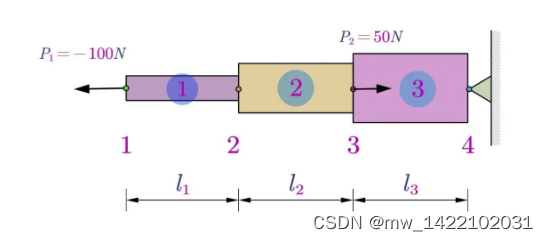
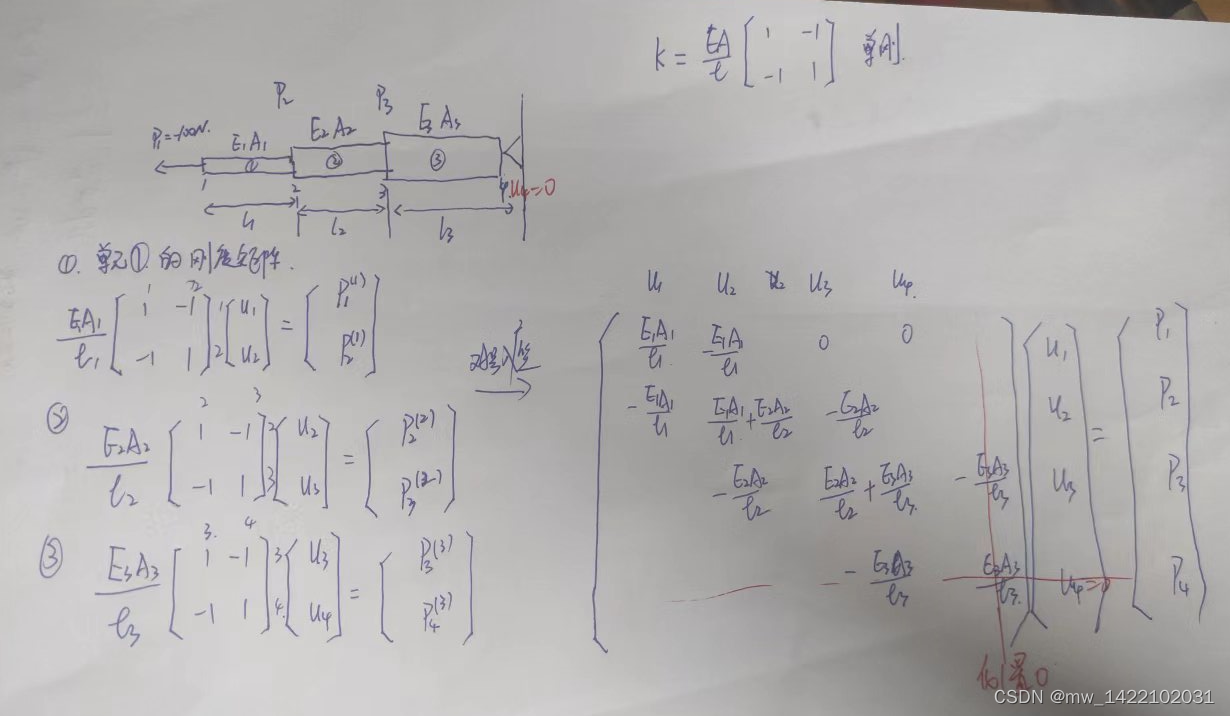
二、编程示例
matlab代码：
function k=Bar1D2Node_Stiffness(E,A,L) %计算单元的刚度矩阵 %输入弹性模量E，横截面积A和长度L %输出单元刚度矩阵k(2X2) %--------------------------------------- k=[E*A/L -E*A/L; -E*A/L E*A/L]; end function z=Bar1D2Node_Assembly(KK,k,i,j) %该函数进行单元刚度矩阵的组装 %输入单元刚度矩阵k，单元的节点编号i、j %输出整体刚度矩阵KK %----------------------------------- DOF(1)=i; DOF(2)=j; for n1=1:2 for n2=1:2 KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); end end z=KK; end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
主函数：
format long % 典型例题[2.3(1)]P17 %弹性模量 E1 = 2*10^5;E2 = E1;E3 = E1; %面积 A3 = 0.06;A2 = 0.5*A3;A1 = A3/3; %长度 L1 = 0.1;L2 = L1;L3 =L1; k1 = Bar1D2Node_Stiffness(E1,A1,L1); k2 = Bar1D2Node_Stiffness(E2,A2,L2); k3 = Bar1D2Node_Stiffness(E3,A3,L3); KK = zeros(4,4); KK = Bar1D2Node_Assembly(KK,k1,1,2); KK = Bar1D2Node_Assembly(KK,k2,2,3); KK = Bar1D2Node_Assembly(KK,k3,3,4); % 直接法求解整体刚度矩阵 k = KK([1:3],[1:3]);%u4 = 0;应用化1置0 p = [-100;0;50]; % 高斯消去法求解线性方程组 u = k\p- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
对代码中单元刚度矩阵组装函数的理解 
将其写成C++程序为: 注意：这个C++程序需要将Eigen库添加到VS中才可以直接用
#include#include using namespace Eigen; using namespace std; MatrixXf Bar1D2Node_Stiffness(float E, float A, float L) { //计算单元刚度矩阵，输入弹性模量E，横截面积A和长度L //输出单元刚度矩阵k(2X2) MatrixXf k(2, 2); //单元刚度矩阵的大小 k << E * A / L, -E * A / L, -E * A / L, E* A / L; return k; } MatrixXf Bar1D2Node_Assembly(MatrixXf KK, MatrixXf k, int i, float j) { //单元刚度矩阵的组装 //输入单元刚度矩阵k，单元的节点编号i、j //输出整体刚度矩阵KK Vector2i Dof; //定义一个2*1的向量 Dof << i, j; for (int n1 = 0; n1 < 2; n1++) { for (int n2 = 0; n2 < 2; n2++) { KK(Dof(n1) - 1, Dof(n2) - 1) = KK(Dof(n1) - 1, Dof(n2) - 1) + k(n1, n2); //注意：c++中数组和矩阵都是从0开始编号的 } } return KK; } int main() { //弹性模量 float E1 = 2e5; float E2 = E1; float E3 = E1; //面积 float A3 = 0.06; float A2 = A3 / 2; float A1 = A3 / 3; //长度 float L1 = 0.1; float L2 = L1; float L3 = L1; //分别计算三个单元的单刚 MatrixXf k1(2, 2); MatrixXf k2(2, 2); MatrixXf k3(2, 2);//将三个单刚初始化 k1 = Bar1D2Node_Stiffness(E1, A1, L1); k2 = Bar1D2Node_Stiffness(E2, A2, L2); k3 = Bar1D2Node_Stiffness(E3, A3, L3); //组装刚度矩阵 MatrixXf KK(4, 4); //总刚的大小 KK.setZero(4, 4); KK = Bar1D2Node_Assembly(KK, k1, 1, 2); KK = Bar1D2Node_Assembly(KK, k2, 2, 3); KK = Bar1D2Node_Assembly(KK, k3, 3, 4); //求解节点位移 MatrixXf kk(3, 3); kk = KK.block<3, 3>(0, 0); //%节点位移u4 = 0;应用化1置0 Vector3f P(-100, 0, 50); //节点力 Vector3f x(0, 0, 0); x = kk.lu().solve(P); //LU分解求解线性方程组kk * x = P system("pause"); return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
程序写的很粗糙，希望之后能够写的有美感
三、二维杆单元
3.1 例题以及基础理论
《有限元基础教程》 39页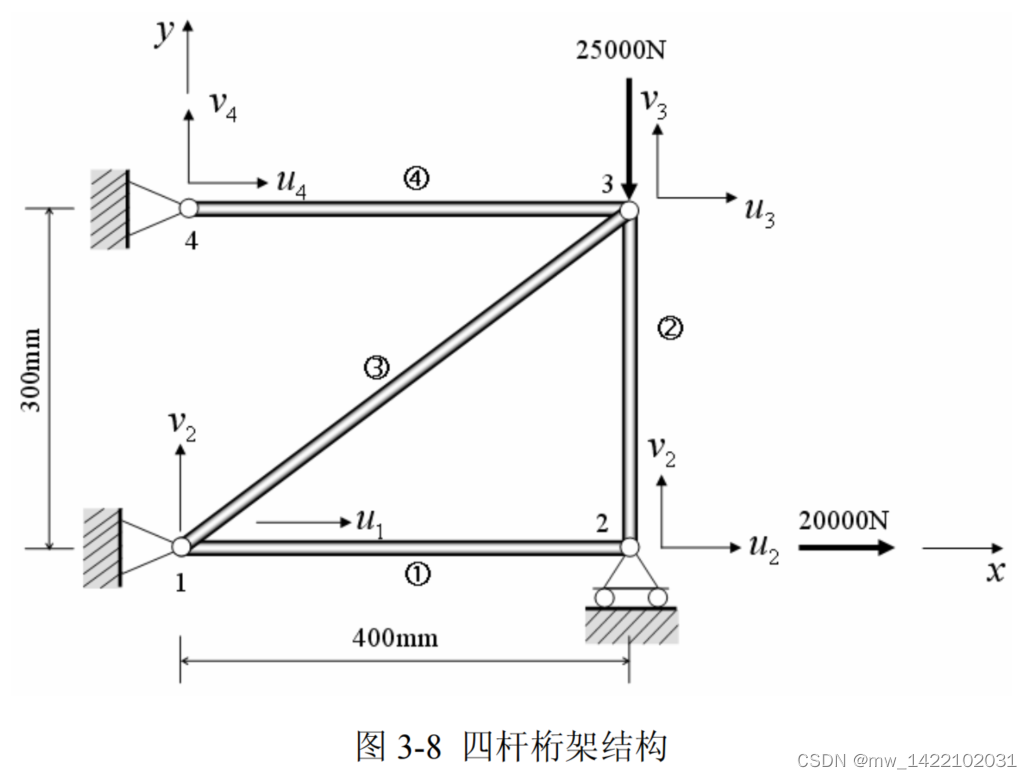  
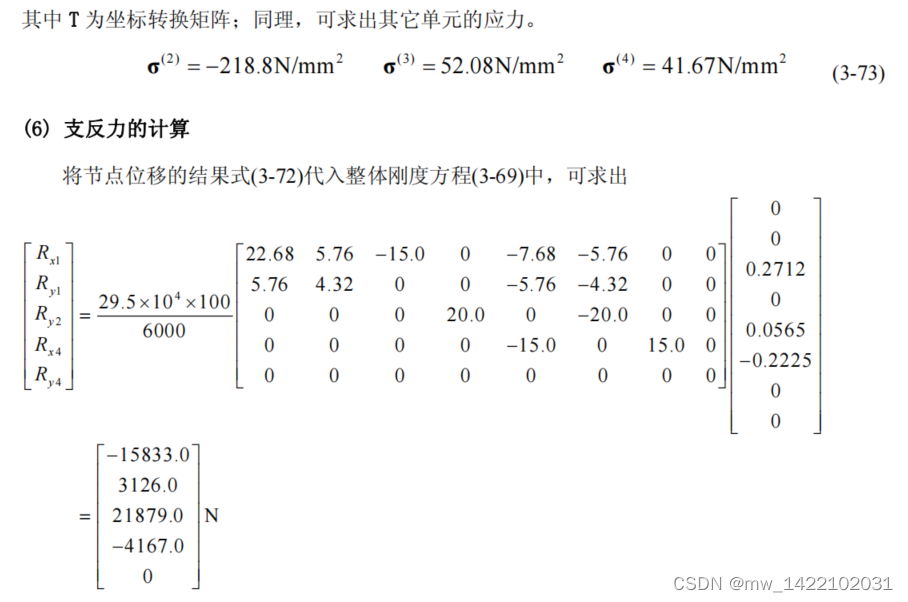
3.2 编程示例
单元刚度矩阵函数 function k=Bar2D2Node_Stiffness(E,A,x1,y1,x2,y2,alpha) %该函数计算单元的刚度矩阵 %输入弹性模量E，横截面积A %输入第一个节点坐标（x1,y1），第二个节点坐标（x2,y2），角度alpha（单位是度） %输出单元刚度矩阵k(4X4)。 L=sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));%杆的长度 x=alpha*pi/180; C=cos(x); S=sin(x); k=E*A/L*[C*C C*S -C*C -C*S C*S S*S -C*S -S*S -C*C -C*S C*C C*S -C*S -S*S C*S S*S]; end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
单元刚度的组装函数 function z = Bar2D2Node_Assembly(KK,k,i,j) %该函数进行单元刚度矩阵的组装 %输入单元刚度矩阵k，单元的节点编号i、j %输出整体刚度矩阵KK DOF(1)=2*i-1; DOF(2)=2*i; DOF(3)=2*j-1; DOF(4)=2*j; for n1=1:4 for n2=1:4 KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); end end z=KK; end- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
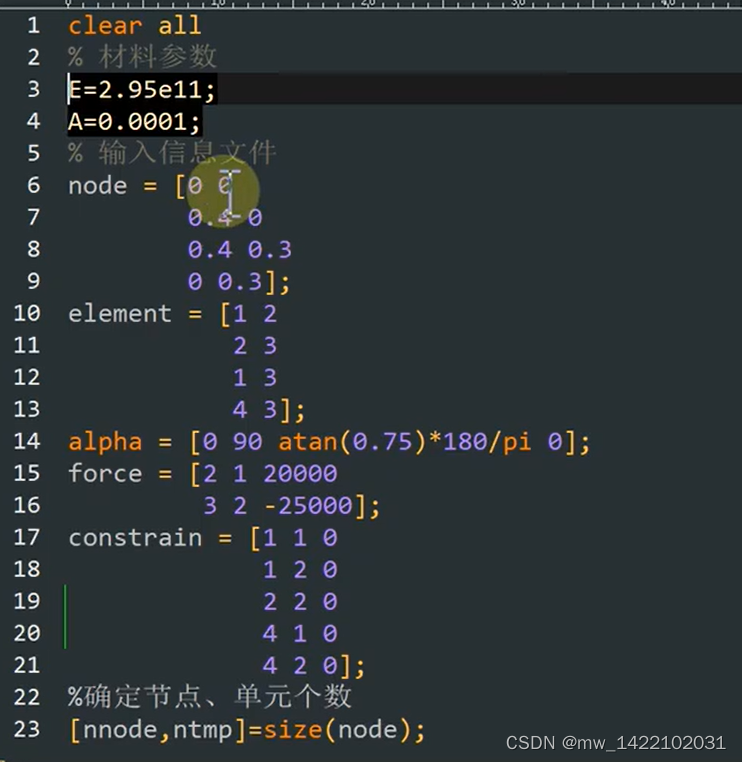
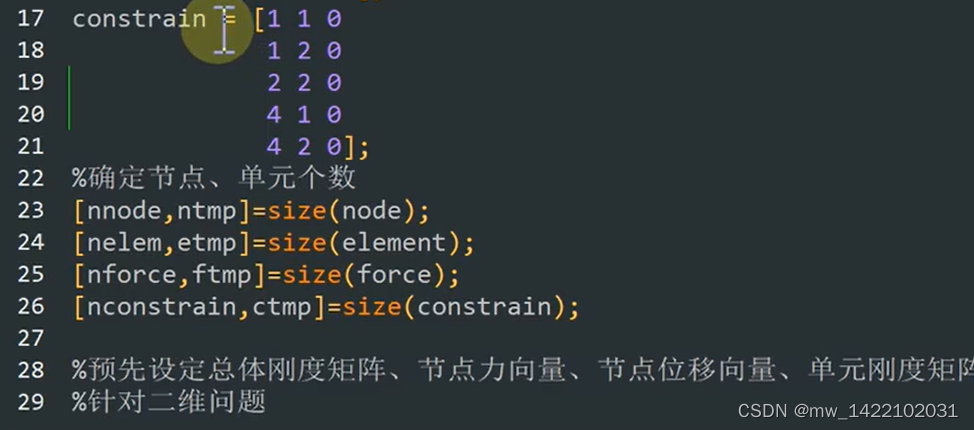
主程序 % 有限元分析及应用简例4.3 %平面杆单元的有限元分析 %给出基础物理量 E=2.95e11;A=0.0001; %给出节点坐标 x1=0;y1=0;x2=0.4;y2=0;x3=0.4;y3=0.3;x4=0;y4=0.3; %给出平面杆的角度，用于求单刚 alpha1=0;alpha2=90;alpha3=atan(0.75)*180/pi; %求每个单元的刚度矩阵 k1=Bar2D2Node_Stiffness (E,A,x1,y1,x2,y2,alpha1) k2=Bar2D2Node_Stiffness (E,A,x2,y2,x3,y3,alpha2) k3=Bar2D2Node_Stiffness (E,A,x1,y1,x3,y3,alpha3) k4=Bar2D2Node_Stiffness (E,A,x4,y4,x3,y3,alpha1) %建立整体刚度方程 %由于该结构共有4个节点，因此，结构总的刚度矩阵为KK(8×8)，先对K清零， %然后四次调用函数Bar2D2Node _Assembly进行刚度矩阵的组装。 KK=zeros(8,8); KK=Bar2D2Node_Assembly (KK,k1,1,2); KK=Bar2D2Node_Assembly (KK,k2,2,3); KK=Bar2D2Node_Assembly (KK,k3,1,3); KK=Bar2D2Node_Assembly (KK,k4,4,3) %边界条件的处理及刚度方程求解 k=KK([3,5,6],[3,5,6]) p=[20000;0;-25000] u=k\p- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
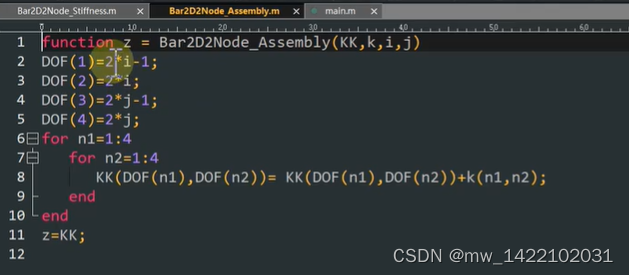
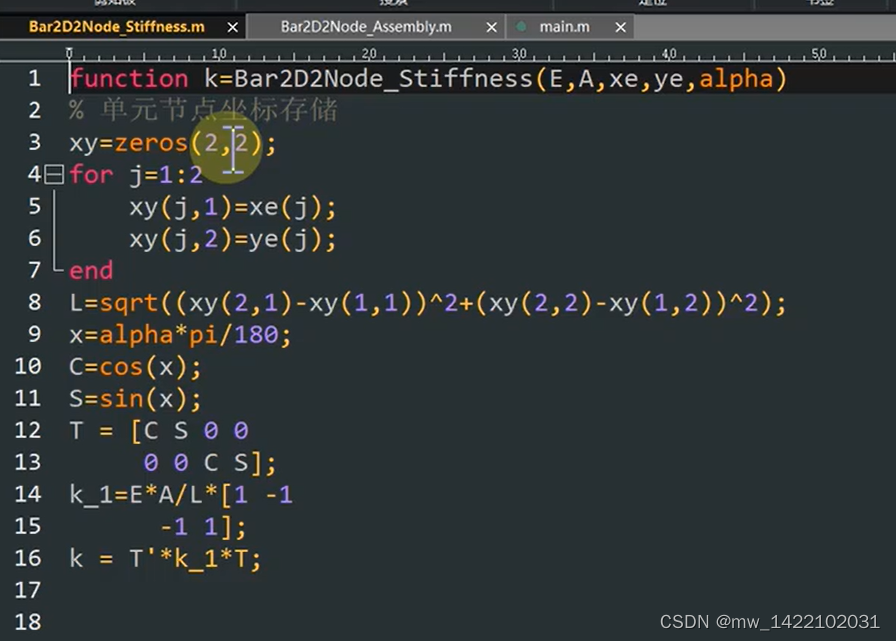
四、平面3节点三角单元分析的算例
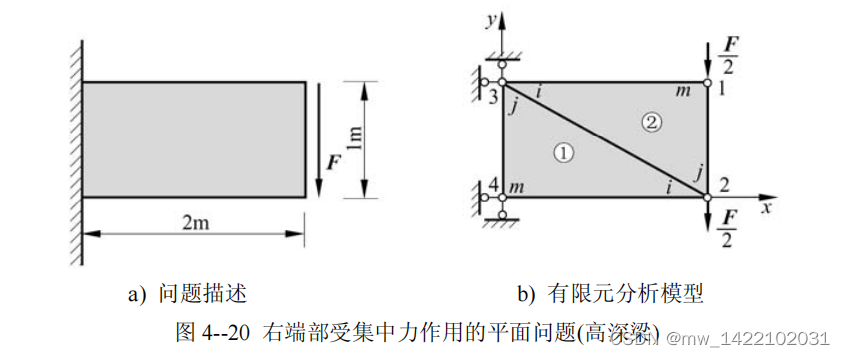
4.1案例分析
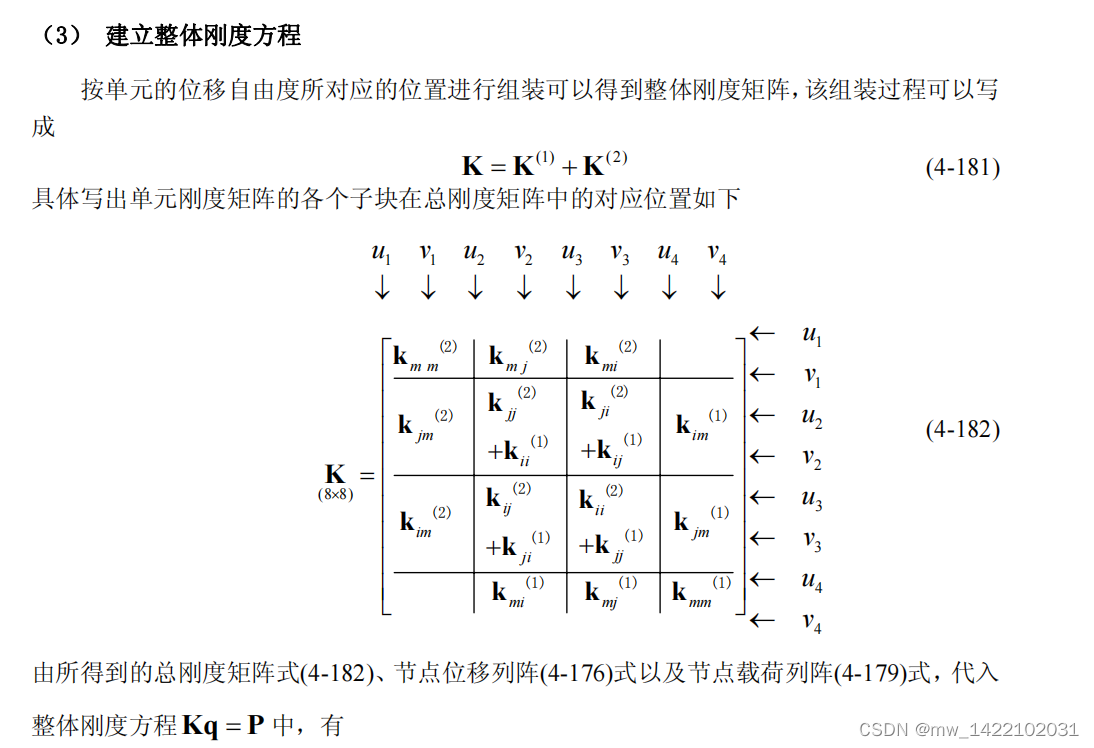
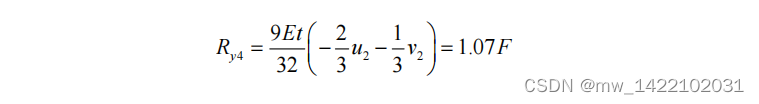
4.2 matlab程序
单元刚度矩阵
function k=Triangle2D3Node_Stiffness(E,NU,t,xi,yi,xj,yj,xm,ym,ID) %该函数计算单元的刚度矩阵 %输入弹性模量E，泊松比NU，厚度t %输入三个节点i、j、m的坐标xi,yi,xj,yj,xm,ym %输入平面问题性质指示参数ID(1为平面应力问题，2为平面应变) %输出单元刚度矩阵k(6X6) %--------------------------------------------------------------- A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2; bi = yj-ym; bj = ym-yi; bm = yi-yj; ci = xm-xj; cj = xi-xm; cm = xj-xi; B = [bi 0 bj 0 bm 0 ; 0 ci 0 cj 0 cm ; ci bi cj bj cm bm]/(2*A); if ID == 1 %平面应力的弹性矩阵 D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2]; elseif ID == 2 %平面应变的弹性矩阵 D = (E/(1+NU)/(1-2*NU))*[1-NU NU 0 ; NU 1-NU 0 ; 0 0 (1-2*NU)/2]; end k= t*A*B'*D*B;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
单元刚度矩阵的组装
function z = Triangle2D3Node_Assembly(KK,k,i,j,m) %该函数进行单元刚度矩阵的组装 %输入单元刚度矩阵k %输入单元的节点编号I、j、m %输出整体刚度矩阵KK %--------------------------------------------------------------- DOF(1)=2*i-1; DOF(2)=2*i; DOF(3)=2*j-1; DOF(4)=2*j; DOF(5)=2*m-1; DOF(6)=2*m; for n1=1:6 for n2=1:6 KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); end end z=KK;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
function stress=Triangle2D3Node_ElementStress(E,NU,xi,yi,xj,yj,xm,ym,u,ID) %该函数计算单元的应力 %输入弹性模量E，泊松比NU，厚度t %输入三个节点i、j、m的坐标xi,yi,xj,yj,xm,ym %输入平面问题性质指示参数ID(1为平面应力，2为平面应变)，单元的位移列阵u(6X1) %输出单元的应力stress(3X1)，由于它为常应力单元，则单元的应力分量为Sx,Sy,Sz %--------------------------------------------------------------- A = (xi*(yj-ym) + xj*(ym-yi) + xm*(yi-yj))/2; bi = yj-ym; bj = ym-yi; bm = yi-yj; ci = xm-xj; cj = xi-xm; cm = xj-xi; B = [bi 0 bj 0 bm 0 ; 0 ci 0 cj 0 cm ; ci bi cj bj cm bm]/(2*A); if ID == 1 D = (E/(1-NU*NU))*[1 NU 0 ; NU 1 0 ; 0 0 (1-NU)/2]; elseif ID == 2 D = (E/(1+NU)/(1-2*NU))*[1-NU NU 0 ; NU 1-NU 0 ; 0 0 (1-2*NU)/2]; end stress = D*B*u;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
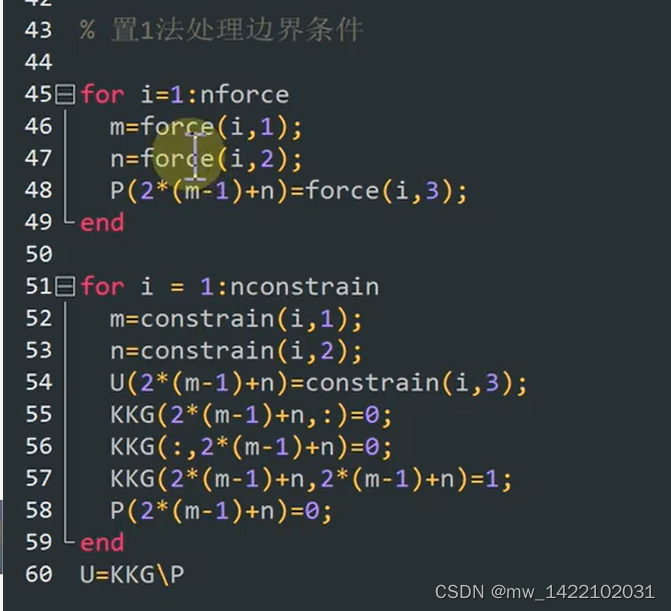
%【MATLAB算例】4.7.1(2) 基于3节点三角形单元的矩形薄板分析(Triangle2D3Node) 143页 %（1）结构的离散化与编号 %（2）计算各单元的刚度矩阵(以国际单位) E=1e7; NU=1/3; %泊松比 t=0.1; ID=1; %输入平面问题性质指示参数ID(1为平面应力问题，2为平面应变)，会给出不同的弹性矩阵D k1=Triangle2D3Node_Stiffness(E,NU,t,2,0,0,1,0,0,ID); k2=Triangle2D3Node_Stiffness(E,NU,t,0,1,2,0,2,1,ID); %（3） 建立整体刚度方程 KK = zeros(8,8); KK=Triangle2D3Node_Assembly(KK,k1,2,3,4); KK=Triangle2D3Node_Assembly(KK,k2,3,2,1); %（4） 边界条件的处理及刚度方程求解 k=KK(1:4,1:4) ; p=[0;-5000;0;-5000]; u=k\p; %节点位移的前四个分量u1，v1，u2，v2 %（5）支反力的计算 U=[u;0;0;0;0]; P=KK*U %（6）各单元的应力计算 u1=[U(3);U(4);U(5);U(6);U(7);U(8)] %第一个单元的应力u2，v2，u3，v3，u4，v4 stress1=Triangle2D3Node_ElementStress(E,NU,2,0,0,1,0,0,u1,ID) u2=[U(5);U(6);U(3);U(4);U(1);U(2)] %第二个单元的应力u1，v1，u2，v2，u3，v3 stress2=Triangle2D3Node_ElementStress(E,NU,0,1,2,0,2,1,u2,ID)- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
4.3 对应的C++程序
#include#include using namespace Eigen; using namespace std; MatrixXf Tri2D3Node_Stiffness(float E, float mu, float t, float xi, float yi, float xj, float yj, float xm, float ym, int Id) { //计算单元刚度矩阵，输入弹性模量E，泊松比NU，厚度t // 输入三个节点i、j、m的坐标xi,yi,xj,yj,xm,ym //输入平面问题性质指示参数ID(1为平面应力问题，2为平面应变) //输出单元刚度矩阵k(6X6) float A, bi, bj, bm, ci, cj, cm; A = (xi * (yj - ym) + xj * (ym - yi) + xm * (yi - yj)) / 2; bi = yj - ym; bj = ym - yi; bm = yi - yj; ci = xm - xj; cj = xi - xm; cm = xj - xi; MatrixXf B(3, 6); B << bi, 0, bj, 0, bm, 0, 0, ci, 0, cj, 0, cm, ci, bi, cj, bj, cm, bm; B = B / (2 * A); MatrixXf D(3, 3); // 弹性矩阵 if (Id == 1) { D << 1, mu, 0, mu, 1, 0, 0, 0, (1 - mu) / 2; D = (E / (1 - mu * mu)) * D; } else if (Id == 2) { D << 1 - mu, mu, 0, mu, 1 - mu, 0, 0, 0, (1 - 2 * mu) / 2; D = (E / (1 + mu) / (1 - 2 * mu)) * D; } //B 矩阵转置：B.transpose() MatrixXf k(6, 6); //单元刚度矩阵的大小 k = t * A * B.transpose() * D * B; return k; } MatrixXf Tri2D3Node_Assembly(MatrixXf KK, MatrixXf k, int i, int j, int m) { //单元刚度矩阵的组装 //输入单元刚度矩阵k，单元的节点编号i、j //输出整体刚度矩阵KK VectorXi Dof(6); //定义一个6*1的向量 Dof << 2 * i - 1, 2 * i, 2 * j - 1, 2 * j, 2 * m - 1, 2 * m; for (int n1 = 0; n1 < 6; n1++) { for (int n2 = 0; n2 < 6; n2++) { KK(Dof(n1) - 1, Dof(n2) - 1) = KK(Dof(n1) - 1, Dof(n2) - 1) + k(n1, n2); //注意：c++中数组和矩阵都是从0开始编号的 } } return KK; } int main() { //初始物理量 float E = 1e7; //弹性模量 float mu = 1.0 / 3; //注意： 不能写成float mu = 1 / 3，这种情况输出结果为0 float t = 0.1; //厚度 int Id = 1; //输入平面问题性质指示参数ID(1为平面应力问题，2为平面应变)，会给出不同的弹性矩阵D MatrixXf k1(6, 6), k2(6, 6); //单元刚度矩阵6*6 k1 = Tri2D3Node_Stiffness(E, mu, t, 2, 0, 0, 1, 0, 0, Id); k2 = Tri2D3Node_Stiffness(E, mu, t, 0, 1, 2, 0, 2, 1, Id); cout << "k1:" << endl << k1 << endl; cout << "k2:" << endl << k2 << endl; //组装刚度矩阵 MatrixXf KK(8, 8); //总刚的大小 KK.setZero(8, 8); //0矩阵 KK = Tri2D3Node_Assembly(KK, k1, 2, 3, 4); KK = Tri2D3Node_Assembly(KK, k2, 3, 2, 1); cout << "总体刚度矩阵 KK = " << endl << KK << endl; //计算节点向量 应用化1置0方法 MatrixXf kk(4, 4); kk = KK.block<4, 4>(0, 0); //节点位移u3,v3,u4,v4 = 0;应用化1置0可以把总刚矩阵简化为kk进行计算 cout << "kk:" << endl << kk << endl; Vector4f p(0, -5000, 0, -5000); //节点力 Vector4f u(0, 0, 0, 0); u = kk.lu().solve(p); //LU分解求解线性方程组kk * x = P cout << "节点位移 u = " << endl << u << endl; //支反力的计算 VectorXf U(8); U << u, 0, 0, 0, 0; //总体节点位移 VectorXf P(8); P = KK * U; cout << "节点位移 U = " << endl << U << endl; cout << "支反力 P = " << endl << P << endl; system("pause"); return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
总结
一维数组名称的用途：
二维数组定义的四种方式: -
相关阅读:
【计网】广播域和冲突域
java毕业生设计学院学生论坛计算机源码+系统+mysql+调试部署+lw
处理普通用户安装启动mysql报Can‘t find error-message file‘usrsharemysqlerrmsg.sys‘ 问题
深入解析HTTPS与HTTP
Python添加水印简简单单，三行代码教你批量添加
WebRTC研究：丢包与抖动
trino的介绍和安装使用
StatefulSets In K8s
Linux之Nginx
数据仓库与数据挖掘实验练习题
- 原文地址：https://blog.csdn.net/mw_1422102031/article/details/126689078
