论文阅读（12） 与其他后生动物相比，水母被动能量的重新获取有助于推进优势（2013）

与其他后生动物相比，水母被动能量的重新获取有助于推进优势 (2014)

原文链接：https://www.pnas.org/doi/10.1073/pnas.1306983110

14年的好文，应该是早期研究水母被动能量捕获的经典论文，文章内容非常精简，建议耐心阅读，我始终觉着水母的运动太美了，不像是这个世界的一种生物一般，它们的运动非常依赖于环境的交互，这让我想起《三体：死神永生》中光速飞船和赫尔辛根默斯肯 的内容，我忽然想到是不是我们生活的陆地世界甚至外太空也应该存在一种类似与水的交互物质呢，现有的仿生科技仍不能实现像鸟类一样灵活的机动羽翼，更别说实现长时间太空漫游的飞船战舰，对于水母的研究一方面是其特有的运动模式蕴含着一种看似优美杂乱却又淡淡地透露出某些细微的规律，另一方面则是尝试研究其身体构造进而学习这种运动方式，这两个方面的实际应用：（1）生产可以高效推进的可长时间续航的海洋探测器；（2）研究其身体构造机理，以无脊椎动物的独有视角来理解运动以及环境交互，提供生态环境保护以及生物医学、工业生产等领域的创新想法。就说这些吧，我感觉说得还是有些模糊，还需要在思考和总结，不啰里啰唆了，接着，努力，奋斗！

摘要

  胶状浮游动物种群以其接管受干扰的生态系统的能力而闻名。这些动物在功能上胜过表现出有效视觉捕食模式的鱼类的能力是违反直觉的，因为水母被描述为效率低下的游泳者，必须依赖与猎物的直接接触才能进食。我们发现，水母表现出一种独特的被动能量再获取机制，这种机制被利用来使它们在每个游泳周期中运动30%，从而减少游泳肌肉对新陈代谢能量的需求。通过解释种间净代谢率的巨大差异，我们证明，与流行的观点相反，水母是地球上最高效的推进器之一，表现出比其他后生动物更低的运输成本(每公斤每米焦耳)。我们估计，通过被动能量再捕获减少新陈代谢需求，可以将运输成本提高48%，使水母能够达到足够的猎物相遇所需的大小。使用计算流体力学和一种新开发的来自经验速度场测量的方法进行的压力计算表明，这种额外的推力是由于在游泳的充水阶段钟形底部的涡环产生的正压力造成的。这些结果表明，尽管水母游泳者的身体规划很简单，但他们在生态上取得成功的物理基础。这项研究的结果对需要低能量推进的生物灵感设计也有意义。
关键词：游泳效率、动物-流体相互作用
重点: 水母有能力繁殖并接管受干扰的生态系统，但这是违反直觉的，因为水母被描述为效率低下的游泳者，依赖与猎物的直接接触来觅食。为了了解水母是如何击败有效的视觉猎人的，我们研究了推进的能量学。我们发现，水母表现出一种独特的被动能量再捕获机制，可以通过游泳减少肌肉对新陈代谢能量的需求。与主流观点相反，这使得水母成为地球上能量最高效的推进器之一。这些结果证明了尽管水母(美杜莎)游泳者的身体规划简单，但他们在生态上取得成功的物理基础，并对需要低能量推进的生物灵感设计具有启示意义。

  在水母游动过程中，加速度在收缩阶段达到，而阻力和减速峰值出现在松弛阶段。因此，研究水母推进的研究主要集中在收缩阶段 (1-4)。胶状浮游动物运动在游泳效率方面的潜在优势以前一直被忽视，因为游泳效率通常使用弗劳德数(E_f) (5-7) 来估计，弗劳德数最初是用来量化船舶推进性能的。E_f的定义是运动过程中产生的有用功率与有用功率加上流体损失的功率之比 (8)。它已被用来比较不同大小和形态的生物物种。之前的研究将水母描述为效率低下的游泳者，E_f值为 0.09-0.53 (5) ，与鱼相比 ≈0.8 (9，10)。然而，这种方法没有考虑游泳净代谢能量需求的巨大种间差异，并且没有将搏动游泳者的放松阶段包括在这样的计算中的协议 (11)。
   一种更全面和与生态相关的估算移动能源成本的方法是运输净成本(COT)分析(图1、A和D)。COT被定义为 $\frac{能量}{质量\times 速度平均值}$ ，它是一个适合于种间游泳效率比较的指标，因为产生运动学和流体运动的能量支出在物种之间并不是恒定的(图1B和C)。通过这一衡量标准，月亮水母 Aurelia aurita 在每单位旅行距离中每单位湿质量所消耗的能量明显低于其他动物。在另一种水母物种(Stomolophus Meleagris)中也报告了表现出低COT的能力 (12)。
  水母怎么能在这么低的COT上游泳，水母物种(Aurelia和Stomolophus)之间的比较和与鱼的比较如何？以另一种高效游泳动物–鲑鱼(Oncorhynchus Nerka)为参照，我们表明,鲑鱼的净COT是Aurelia的3.5倍，Stomolophus的净COT是Aurelia的两倍或更多(图1D)。Aurelia较低的COT主要是由于其游泳的净代谢率较低，比Stomolophus低15倍(图1C)。
   水母可以表现出如此低的呼吸频率，这是因为游泳时代谢不活跃的组织所占比例很大。与其他游泳者相比，水母的身体碳含量较低 (13) ，这导致肌肉在身体质量的含量≤1% (12，14)。相比之下，鱼的身体质量是≥50%的肌肉 (15)。消耗如此少的能量来产生推力，对胶状浮游动物来说是一种适应优势。 然而，考虑一下权衡。低碳和肌肉质量限制了水母的推进选择 (16) 。由于胶状浮游动物的肌肉质量低，他们只能以低速度游泳，而突发性游泳速度仅比常规游泳高30%，因此失去了游泳熟练程度 [12]。低速度通常会增加COT；然而，在水母中，这一点被低代谢需求所弥补。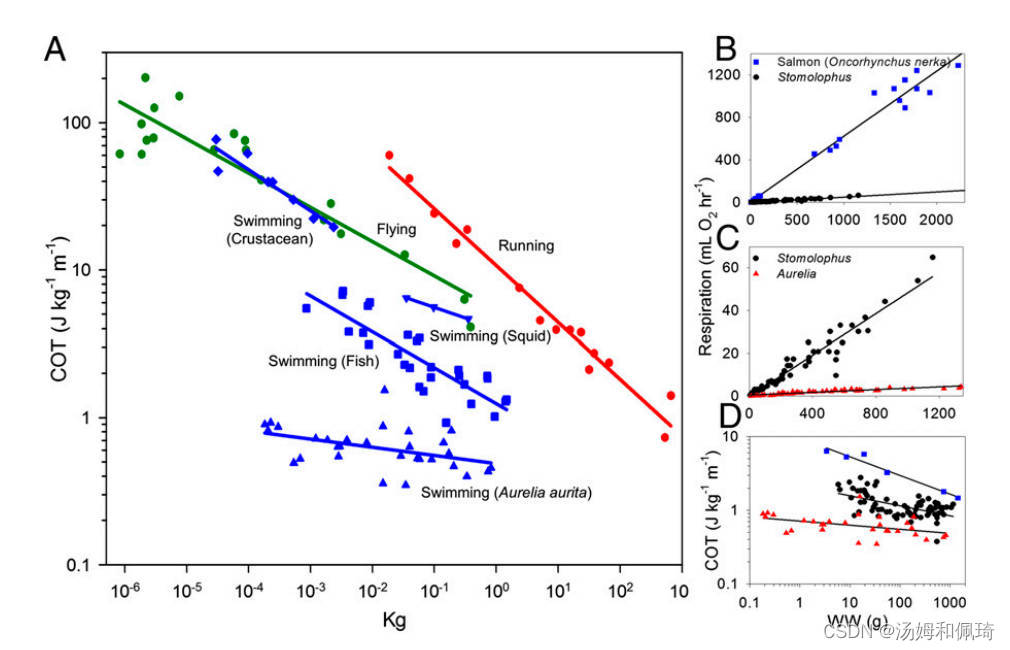

图1 推进模式的高能游泳比较。 (A) 基于湿重的净 COT。 Schmidt-Nielsen (30) 从研究中重新绘制了飞行者和跑步者的数据。甲壳类动物和鱿鱼是从 Larson (12) 的研究中重新绘制的。将这两项研究的鱼类数据结合起来 (12,30)。 A. aurita 的数据是根据当前研究的游泳速度与体型计算得出的，并补充了 Martin (27) 和 McHenry 和 Jed (28) 的研究数据以及 Uye 和 Shimauchi (29) 研究的代谢数据）。 (B) 鲑鱼 (O. nerka) 和根茎水母 (S. meleagris) 的运动净呼吸速率。 （C）S. meleagris 和 A. aurita 的运动净呼吸速率。 (D) 所有三个物种的净 COT。用于鲑鱼呼吸和 COT 的数据来自 Brett 和 Glass (31)的研究，而 Stomolophus 数据是从 Larson (32) 的研究中重新绘制的。 WW，湿重。

  
  虽然低肌肉质量限制了水母在收缩过程中产生的推力 (16，17) ，但我们证明了水母使用一种被动能量重新捕获的形式来增强它们的游泳能力，并进一步减少它们的COT。钟形收缩在钟形边缘产生起始涡，在起始涡 (11) 的上游形成具有反号涡度的停止涡。在开始的旋涡脱落后，松弛或重新填充阶段开始，并在将流体拉到铃声下时加强停止旋涡循环和涡度(图2a和电影S1)。尽管水母在收缩过程中表现出更大的加速度和峰值速度(图2B和图3)。如图1)所示，停止涡(与产生的推力成正比)的峰值环流可能比起始涡(图2a)大得多(ANOVA，P=0.01；n=10)，这说明了在游泳过程中停止涡的潜在重要性。一项使用计算流体动力学(CFD)的研究先前已经证明，在再填充(松弛)阶段产生能量 (18)，但对效率和距离的相对贡献尚不清楚。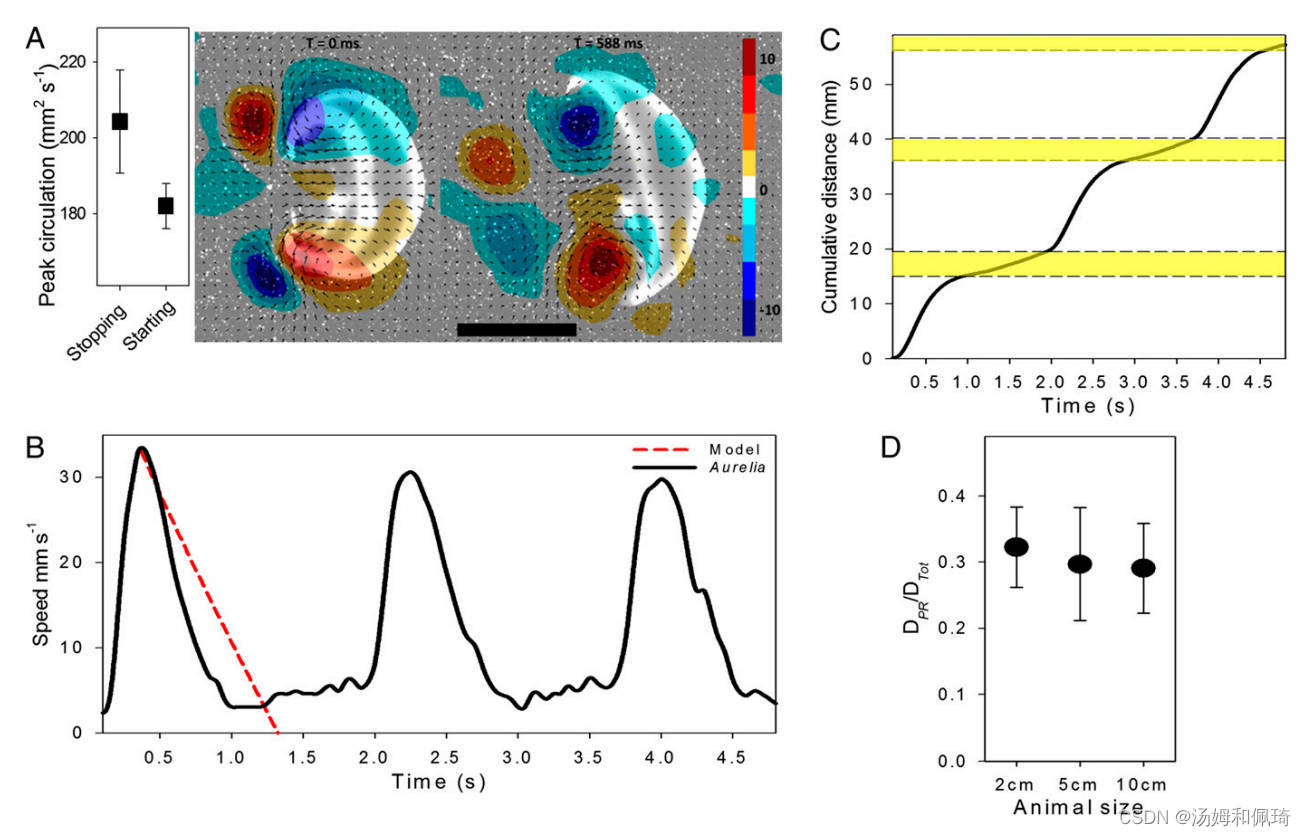

图2 A. aurita 的游泳表演。 (A) 正常游泳（巡航）期间的最大循环和涡量开始和停止涡流。 （比例尺，1 厘米。）（B） 3 厘米 A. aurita 的代表性游泳序列，显示在无运动身体运动期间（恢复后）速度增加。模型（红色）显示了仅来自惯性的速度随时间变化的保守估计。 (C) B 中所示水母的累积距离。黄色表示从被动能量回收中获得的距离。 (D) 被动能量回收与尺寸（钟形直径）的影响。在体型和被动能量回收 (D_PR) 的距离与每次游泳行程的总距离 (D_Tot) 之间的关系之间没有观察到差异 (P = 0.550)。

  
  水母的中胚层组织具有粘弹性 (19) 和弹性 (20) 。然而，负责二次推力的充填阶段被发现完全来自中胚层 (20) 的弹性性质(图2)。S2)。该弹性组织内的应力-应变关系呈现非线性的J型关系 (21，22) 。这使得组织在收缩开始时，当流体动力输出的潜力很高时，可以很容易地应变，并在收缩结束时储存大部分应变能量。这有助于优化能量效率，因为在加速期间，几乎所有的能量都用于产生推力，而弹性应变存储主要发生在收缩周期的末尾。因此，只使用储存的应变能量，而不使用来自对抗肌群的额外能量，就产生了大的停止涡旋并将其定位在铃声下方。 对多种水母的研究表明，在水母的每个游泳周期中，只有一小部分(∼20%)需要肌肉收缩(图3A-C)。使收缩钟减速所需的能量被转化为重新填充钟，类似于飞行昆虫所展示的机制，这大大降低了推力生产的能量成本 (23)。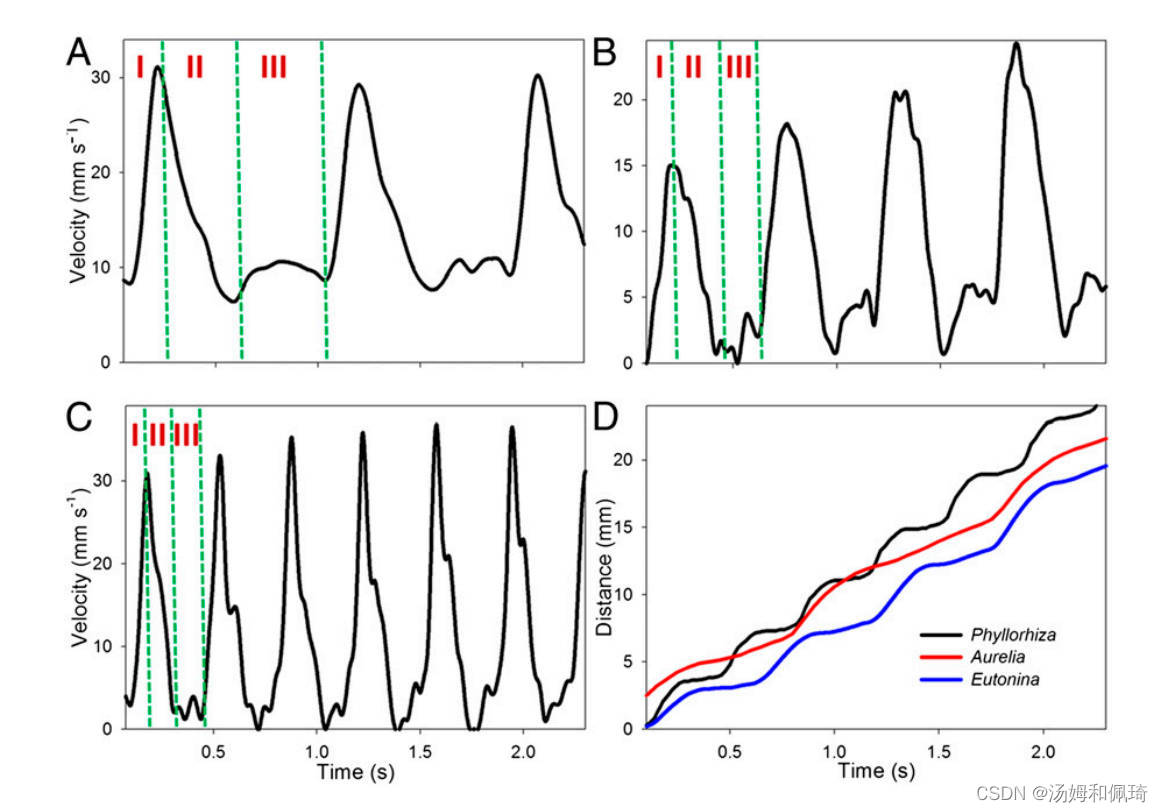

图3三种水母的游泳表现在收缩持续时间(I)、松弛/再充盈持续时间(II)和被动能量重新捕获所产生的推力的脉间持续时间(III)上表现出物种差异。这三个物种在第三阶段都表现出更强的推力。(A) 扁平钵水母, A. aurita; (B)水螅水母, Eutonina indicans;(C) 根口水母, Phyllorhiza punctata。(D)所有三个物种的累积游泳距离。

  
  我们的结果表明，每个脉冲总行程的32%(SD=0.6%)可以发生在松弛后阶段(脉间阶段)，在此期间动物不会产生运动性运动(即滑行)，而在惯性运动之后将停止(图2B和C)。麻醉的A. aurita以自然的游泳速度被人为地向前推进，以便能够观察到超过随后正常开始收缩的持续时间的停止涡旋的影响。我们表明，被动的钟声补充可以在钟声运动停止后的较长时间内产生推力(图3)。S2)。所产生的力量可以在每个脉冲中额外携带10.1毫米(SD=0.8，n=4)的4厘米Aurelia，这是在正常游泳的运动活跃部分所测得的12.7毫米(SD=3.5，n=5)的80%。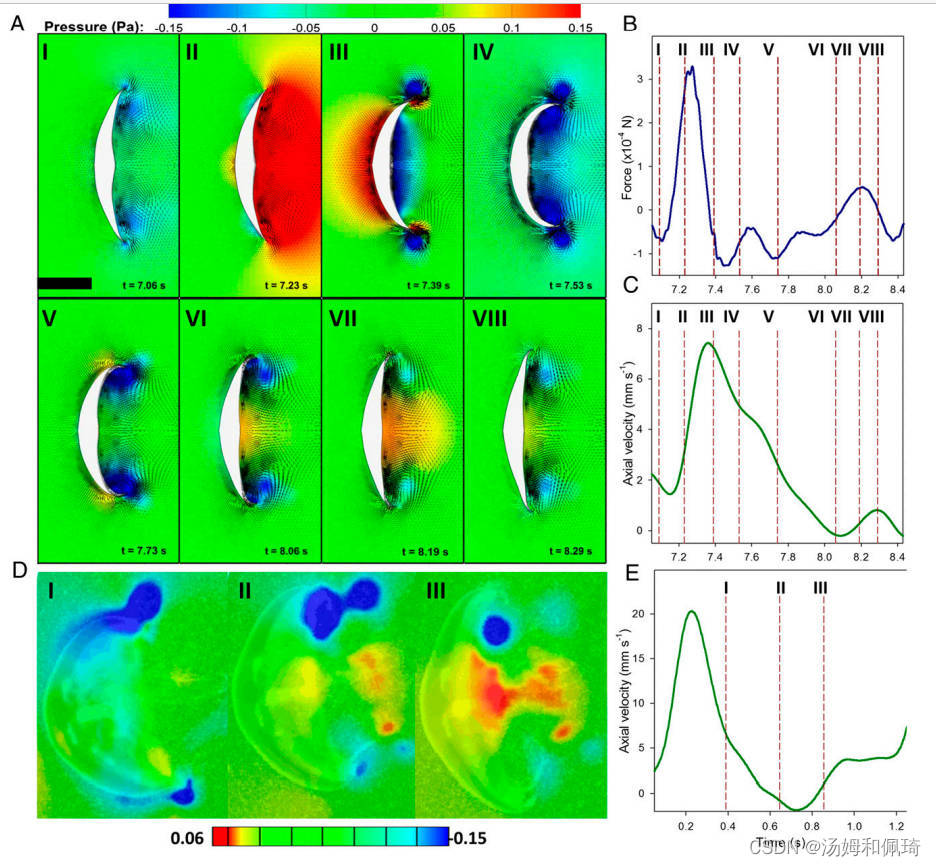

图4 3 厘米游泳 A. aurita 的 CFD。(不太清晰,建议查找原文看原图) (A) 游泳循环期间身体周围的压力。注意伞下表面 (VI-VIII) 压力的二次增加以及由此产生的轴向力和速度增加。 (B) 轴向力显示了 A 中的相应位置。显示了对应于由停止涡流累积在伞下表面产生的诱导流的正压力的次峰。 (C) 速度时间图显示了 A 中的相应位置。(D) 来自 3.5 厘米 A. aurita 周围速度场测量的压力估计经验技术的结果。 (E) 速度-时间图显示了 D 中的相应位置。

  
  为了解释钟声重新充气后推力是如何产生的，我们使用CFD和一种新开发的根据速度场测量来估计压力的经验技术相结合，测量了水母身体周围的压力。与喷射的脊髓相比，扁平的脊髓在伞下表面产生更复杂的压力场 (24)。我们发现，在钟形松弛期间，压力通常很低，因为发生了再灌装，但随后从停止涡旋产生的诱导流动对伞下表面形成，并在涡环的低压核心之间产生了一个大范围的正压区域(图4和电影S2)。由此产生的高压产生了足够的力，使身体在最初收缩之后和下一个周期之前产生额外的加速度(图4B和C)。
  可以做出一个简单、保守的估计，以理解被动能量再捕获如何对Aurelia的COT做出贡献。消除脉冲间持续时间(以及因此被动能量重新捕获的任何影响)将导致脉冲频率在$\frac{T_{i}p}{T_{t}ot}=0.50$ (SD=0.05，n=20)时加倍，其中T_ip是脉冲间持续时间的时间，T_tot是每个脉冲的总时间。尽管水母的脉搏频率和呼吸之间的关系尚不清楚，但对于水母来说，它是指数关系 (25) 。保守地，我们假设呼吸频率和脉冲频率之间存在线性关系。通过对直径2-10厘米的动物(V_A/V_T=1.35，n=12)在游泳周期活动期(V_A)测得的速度与总速度(V_T)进行比较，我们发现COT至少会增加$\frac{2个能量}{质量\times (1.35\times 速度)}=1.48$ 倍，如果不使用被动能量再捕获，COT将增加48%。 (被动能量捕获起到了非常大的占比,可以极大地缓解该物种极低代谢率的副作用影响.)
  尽管刺胞动物的游泳肌肉结构和力量产生与其他动物群相似 (16)，但刺胞动物的肌肉纤维仅位于上皮肌肉细胞内。这个单细胞层限制了刺胞动物游泳肌肉的厚度，从而在水母游泳期间产生了力量。因此，超过一定大小，并且与其他动物不同，水母不会继续随着大小增加游泳速度。因此，随着身体大小继续增加游泳速度所需的额外力量仅限于水母的特定范围。这对 COT 有影响，因为水母在很小的时候似乎比其他后生动物具有最大的优势。然而，从图 1 推断结果表明，在体重超过 ~100 kg 时，鱼的 COT 才开始低于 Aurelia。
  水母使用被动能量再捕获的能力减少了新陈代谢需求，同时增加了摄食结构所遇到的液体(因此是猎物)，并转化为可用于生长和繁殖的更多能量。这种能量优势将使水母种群能够利用猎物过剩的环境，并有助于证明一些水母物种有能力在短时间内迅速繁殖并胜过其他物种，如鱼类 (26)。我们的结果表明，由于COT仅在水母中就可能变化两倍以上，在试图理解水华动力学和营养竞争时，应该考虑被动能量再捕获对物种的特定影响。此外，在仿生设计中，Aurelia所展示的被动能量回收可能是一个重要的考虑因素，因为仿生设计需要低能量需求来进行有效的车辆设计。被动能量回收似乎与动物的大小有很好的比例关系，这一事实也表明，在广泛的大小范围内，有重要的设计意义有待探索。

材料与方法

游泳运动学

  自由游动的水母(1.5~6 cm)在玻璃摄像容器(30×10×25 cm)中以1000帧/秒的速度被高速数码摄像机(Fastcam 1024PCI；Photron)记录下来。在分析中只使用了动物向上游泳的记录，以消除重力帮助动物在脉冲之间向前运动的可能性。使用Image J v1.46软件(美国国立卫生研究院)跟踪水母钟尖和钟缘尖端的x和y坐标，获得详细的游泳运动学(2D)。游泳速度是根据顶点位置随时间的变化计算出来的，公式如下：

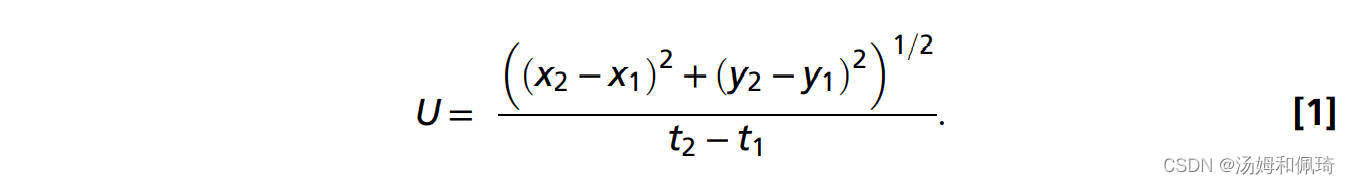
  水母用垂直于相机光轴的激光(680 nm，2W连续波；LaVision)照射，为图像分析提供独特的身体轮廓，并确保动物保持在平面内，从而确保2D位置和速度估计的准确性。在新英格兰水族馆的专用展览箱中，使用高清晰度索尼HDV Handycam(型号HDR-FX1)获得了大型(>6厘米)金鱼的游泳运动学数据。在这里，一个500毫瓦的激光(432 nm，大力神系列；激光辉光)被形成一张薄片，从上面照射动物的轮廓，用于运动学分析。

COT.

  根据特定质量的游泳速度和呼吸速率估计了月亮水母(A.aurita)每单位质量和距离的代谢COT(焦耳/千克/米)。特定质量的游泳速度来自运动学数据(当前研究)，并补充了Martin (27) 和McHenry和Jed (28) 的研究数据。从Uye和Shimuchi (29) 获得了A.aurita的群体比活动呼吸数据。代谢呼吸到能量消耗(焦耳)的转换是由O₂ (12) 的19 J·mL⁻¹的转换系数完成的。为了获得仅占用于运动的能量消耗的净COT，必须从活动率中减去基本能量消耗。因为基础频率被发现是水母的一半活跃频率 (12)，所以我们计算出在水母中专用于定位的能量比例是活跃频率的0.5倍。应该注意的是，这使得我们的A.aurita 净COT估计是保守的，因为A.aurita的脉动率比所研究的物种低 (12) 。这是因为与许多其他物种相比，水母花在主动收缩上的时间成比例地更少(图3)。由于这是唯一一次用于游泳，由于被动放松 (19)，A.aurita(和COT)的主动代谢率占总代谢率的比例可能会更低。鲑鱼 (30) 的质量比呼吸和游泳数据用于比较目的。
  使用以下公式计算净COT：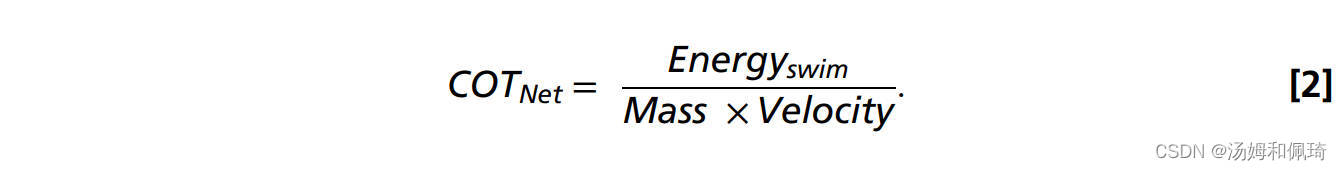

  使用图形数字化软件(GetData v2.25)，从Larson (12)、Uye和Shimuchi ==(29)==和SchmidtNielsen ==(30)==的研究中获得并重新绘制用于跑步者、飞行员和其他游泳运动员的净COT。

游泳水母周围的流体性质

  使用2D数字粒子图像测速仪对水母在游泳时产生的流体运动进行量化。使用上述装置，在过滤后的海水中加入10 μm的中空玻璃微珠。通过使用互相关算法(LaVision软件)分析的序列图像来确定在激光片中照射的粒子的速度。通过将重叠询问窗口从64×64像素减小到32×32像素或将32×32像素减小到16×16像素来分析图像对。有关循环和压力估计的详细信息，请参阅SI材料和方法**。运动学数据被对数变换，并使用Shapiro-Wilks检验进行正态检验**。随后使用单因素方差分析对数据进行检验，以确定均值之间是否存在显著差异。

游泳水母的CFD模型

  我们利用直径3厘米的自由游动月亮水母(A.aurita)的钟形运动学建立了一个水母模型。沿着身体这一半的数字化点使用八阶多项式进行空间内插，使用巴特沃斯滤波器进行时间平滑，以及使用三次样条多项式(图2)进行时间内插。S3)。
  采用大型商用软件–FLUENT 13.0，对非定常、不可压缩、轴对称的N-S方程进行了数值模拟。通过将水母的向前运动与施加在铃铛上的水动力耦合来模拟游泳。在每个时间步长结束时，沿轴向作用于水母表面的压力和剪切力被积分，并计算得到的物体加速度。力平衡的离散形式由以下公式给出：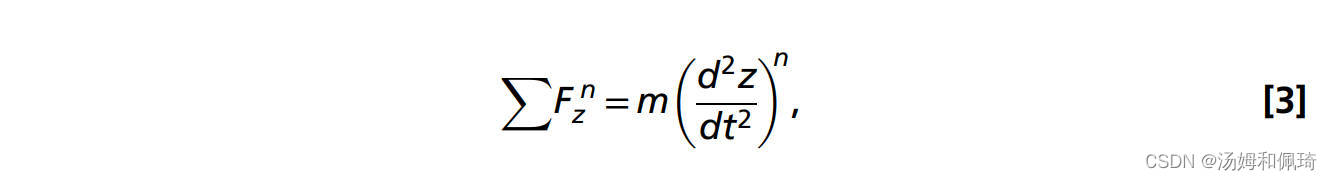

其中$\sum F_z^n$是在时间步长n的轴向上所有压力和剪力的总和，m是水母的质量(假定流体密度与周围的水相同：* ρ*=998.2 kg·m⁻³)，以及$(\frac{d^{2}z}{d{t}^2}{)}^n$是水母质心处的轴向加速度。利用泰勒级数展开，加速度可以用二阶精度近似，

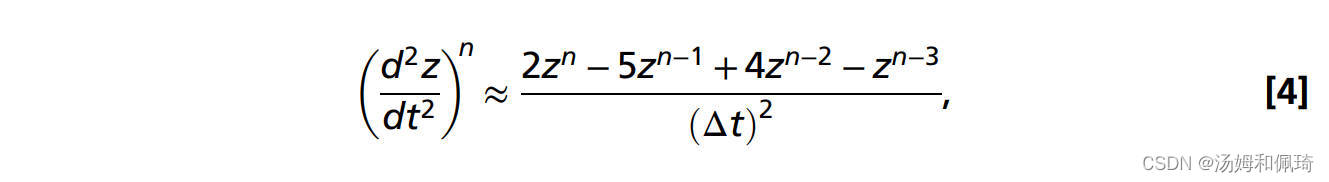
其中z是轴向位移，Δt是时间步长。结合方程7和8，时间步长n处的位移可以近似为：

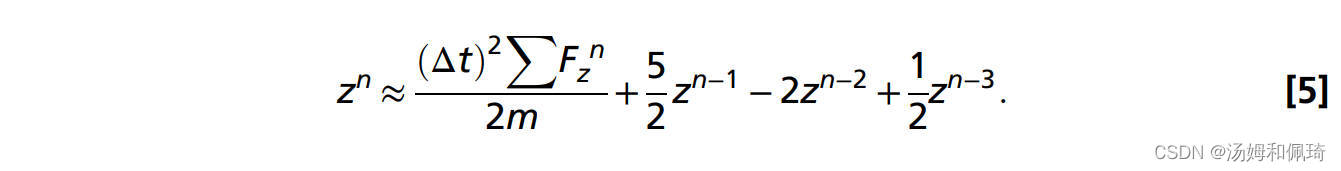
最后，为了确保解算器和水母置换之间的稳定耦合，我们使用指数加权移动平均来平滑原始置换zⁿ：

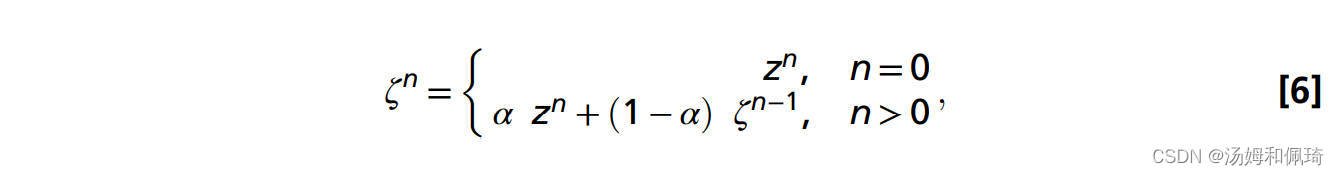
其中ζ是指定给水母的平滑置换，$\alpha \in [0,1]$ 是平滑系数。我们发现，鲁棒的模拟需要 α=0.25。
  进行了验证和验证研究，以确保我们的模拟的数值和物理精度。我们首先检查了我们的结果对网格和时间步长细化的敏感性(图3)。S4)。一个由60,895个细胞组成的基本网格(顶部和底部钟形轮廓上分别有64和58个细胞面)被细化到135,765个细胞(顶部和底部钟形轮廓上分别有86和82个细胞面)，结果表明作用在水母上的力的总和以及它的游泳性能对空间细化不敏感。同样，使用从Δt=1/90 s到Δt=1/180 s的时间步长进行模拟，没有导致作用在水母上的水动力发生明显变化。其次，将数值水母的瞬时位移与用于游泳运动学的天然水母的瞬时位移进行了比较(图3)。S5)。两者在整个游泳期表现出相似的趋势和相似的速度，导致几乎相同的总排水量。