PySpark数据分析基础：pyspark.mllib.regression机器学习回归核心类详解(一)+代码详解

目录

前言

一、Spark MLlib

二、回归类

1.LabeledPoint

2.LinearModel

3.LinearRegressionModel

load方法

 predict方法

save方法

4.LinearRegressionWithSGD

train方法

点关注，防走丢，如有纰漏之处，请留言指教，非常感谢

---

前言

PySpark数据分析基础系列文章更新有一段时间了，其中环境搭建和各个组件部署都已经完成。借此征文活动我将继续更新Pyspark这一大块内容的主体部分，也是十分重要且比较难懂不易编程的部分。在从事大数据计算以及分析的这段历程中，陪伴我最多的也就是anaconda和Jupyter了，当然此次演示还是用到这些工具，文章紧接此系列的上篇文章内容。若将来想要从事数据挖掘和大数据分析的相关职业，不妨可以关注博主和订阅博主的一些专栏，我将承诺每篇文章将用心纂写长期维护，尽可能输出毕生所学结合如今先有案例项目和技术将每个知识点都讲明白清楚。

希望读者看完能够在评论区提出错误或者看法，博主会长期维护博客做及时更新。

---

虽然我们讲的是Pyspark MLlib某个片段内容，但是是整个系列的第一次讲述Spark MLlib，所以首先还是对整Spark做一个简要的概述。

一、Spark MLlib

MLlib构建在Spark之上，是一个可扩展的机器学习库，它提供了一组统一的高级API，帮助用户创建和调整实用的机器学习管道。MLBase分为四部分：MLlib、MLI、ML Optimizer和MLRuntime。

•     ML Optimizer会选择它认为最适合的已经在内部实现好了的机器学习算法和相关参数，来处理用户输入的数据，并返回模型或别的帮助分析的结果；
•     MLI 是一个进行特征抽取和高级ML编程抽象的算法实现的API或平台；
•     MLlib是Spark实现一些常见的机器学习算法和实用程序，包括分类、回归、聚类、协同过滤、降维以及底层优化，该算法可以进行可扩充； MLRuntime 基于Spark计算框架，将Spark的分布式计算应用到机器学习领域。

PySpark可以直接调用spark几乎大部分的函数和接口，操作代码十分方便。根据机器学习的需要，spark有一整个机器学习的包可以调用，类似python的sklearn一样。调用相关函数即可实现对应功能，而且在分布式基础之上计算能力会更加卓越。

二、回归类

1.LabeledPoint

该类用于添加或者构建数据集测试非常好用，该类可以生成一条带有特征和标签的数据集。

函数语法：

LabeledPoint(label: float, features: Iterable[float])

 参数说明:

• label：接收int类型，指定数据的标签
• features：可以接收pyspark.mllib.linalg.Vector或者是数组。

使用实例：

data = [
    LabeledPoint(0.0, [0.0, 1.0,2.0]),
    LabeledPoint(1.0, [1.0, 0.0,2.0]),
]

这样就创建了一个小型数据集，可以通过random加上循环构建出随机测试数据集。

2.LinearModel

生成一个具有系数向量和截距的线性模型。

函数语法：

LinearModel(weights: pyspark.mllib.linalg.Vector, intercept: float)

参数说明：

• weights:接收pyspark.mllib.linalg.Vector或者是数组，指定权重。
• intercept:接收float类型，为该模型计算的截距。

使用实例：

lrm = LinearModel([0.2,0.5,0.8],intercept=0.2)

这个函数没有子方法，实际运用起来也很少，几乎用处不大。

3.LinearRegressionModel

生成一个由最小二乘拟合得出的线性回归模型。python的线性拟合都是依据最小二乘法来拟合的。

函数语法:

LinearRegressionModel(weights: pyspark.mllib.linalg.Vector, intercept: float)

 和线性模型的参数一样：

• label：接收int类型，指定数据的标签
• features：可以接收pyspark.mllib.linalg.Vector或者是数组。

但是该函数拥有三个子方法：

• load(sc, path):登陆一个LinearRegressionModel模型。
• predict(x):预测给定向量或包含自变量值的向量RDD的因变量值。
• save(x):保存一个LinearRegressionModel模型。

load方法

load(sc: pyspark.context.SparkContext, path: str)

参数说明：

sc:输入指定的SparkContext。

path:输入指定的路径名称。

 
sameModel = LinearRegressionModel.load(sc, path)

 predict方法

语法：

predict(x: Union[VectorLike, pyspark.rdd.RDD[VectorLike]]) → Union[float, pyspark.rdd.RDD[float]]

预测给定向量或包含自变量值的向量RDD的因变量值。

参数说明：

x：输入向量以及RDD数据或者是小数加上RDD数据

lrm = LinearRegressionModel([0.2],intercept=3)
lrm.predict([0.2])

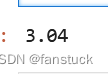
save方法

语法：

save(sc: pyspark.context.SparkContext, path: str)

 保存一个LinearRegressionModel模型。

4.LinearRegressionWithSGD

生成一个使用随机梯度下降训练无正则化的线性回归模型。

SGD的含义就是Stochastic Gradient Descent (SGD)，随机梯度下降。该模型通过train方法训练。

train方法

classmethod train(data: pyspark.rdd.RDD[pyspark.mllib.regression.LabeledPoint],
                  iterations: int = 100, 
                  step: float = 1.0, 
                  miniBatchFraction: float = 1.0, 
                  initialWeights: Optional[VectorLike] = None,
                  regParam: float = 0.0,
                  regType: Optional[str] = None,
                  intercept: bool = False,
                  validateData: bool = True,
                  convergenceTol: float = 0.001) 
 → pyspark.mllib.regression.LinearRegressionModel

 使用随机梯度下降（SGD）训练线性回归模型解决了最小二乘回归公式：

的均方误差。数据矩阵有n行，输入RDD保存A的行集合，每个行都有相应的右侧标签y。

参数说明：

• data：接收类型为Pyspark.RDD。指定训练用到的数据集，可以是LabeledPoint的RDD。
• iterations：接收类型为int，指定迭代次数。
• step：接收类型为float，SGD中使用的阶跃参数，默认为1.0。
• miniBatchFraction：接收类型为float，用于每次SGD迭代的数据部分，默认为1.0.
• initialWeights：接收类型为pyspark.mllib.linalg.Vector，指定初始权重。
• regParam：接收类型为float，为正则化参数。默认为0.0.
• regType：接收类型为str，用于训练模型的正则化子类型。
  • 使用l1正则化：“l1”
  • 使用l2正则化：“l2”
  • 若为None则表示无正则化(默认)
• intercept：接收类型为bool，指示是否使用训练数据的增强表示（即是否激活偏差特征）。（默认值：False）
• validateData：接收类型为bool，指示算法是否应在训练前验证数据。（默认值：True）
• convergenceTol：接收类型为float，决定迭代终止的条件。（默认值：0.001）

data = [
    LabeledPoint(0.0, [0.0]),
    LabeledPoint(1.0, [1.0]),
    LabeledPoint(3.0, [2.0]),
    LabeledPoint(2.0, [3.0])
]
lrm = LinearRegressionWithSGD.train(sc.parallelize(data), iterations=10,initialWeights=np.array([1.0]))
lrm.predict(np.array([0.0]))

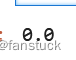
同样化为SparseVector也是一样：

data = [
    LabeledPoint(0.0, SparseVector(1, {0: 0.0})),
    LabeledPoint(1.0, SparseVector(1, {0: 1.0})),
    LabeledPoint(3.0, SparseVector(1, {0: 2.0})),
    LabeledPoint(2.0, SparseVector(1, {0: 3.0}))
]
lrm = LinearRegressionWithSGD.train(sc.parallelize(data), iterations=10,initialWeights=np.array([1.0]))
lrm.predict(np.array([0.0]))

 

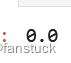
点关注，防走丢，如有纰漏之处，请留言指教，非常感谢

以上就是本期全部内容。我是fanstuck ，有问题大家随时留言讨论 ，我们下期见。